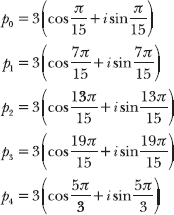Square roots, cube roots, etc.
18.40 State the formula used to calculate the nth roots of complex number z = r(cos θ + isin θ) and explain how to apply it.
The number of nth roots of a complex number is equal to n. For example, if you are calculating square roots, then there are exactly n = 2 square roots of z. Similarly, there are exactly n = 3 cube roots of z. These roots are evenly spaced around the unit circle according to the following formula.
In the formula, pk represents one root. The subscript merely numbers the roots, from 0 to n – 1. For example, when you calculate cube roots using this formula, n = 3 and the names of the cube roots are p0, p1, and p2. The highest subscript is 2, which is exactly one less than n = 3.
Calculating roots is not complicated if you keep these facts in mind:
• Each root has the same modulus, 
. Only the arguments of the roots vary.
• The argument of the first root, p0, is equal to θ/n.
If you substitute k = 0 into 
, you get 
.
• To calculate the remaining arguments, add 360°/n to the first argument.
Note: In Problems 18.41–18.42, c = 16(cos 100° + isin 100°).
18.41 Determine how many square roots exist for c and calculate the square root with the smallest argument.
You are asked to calculate the square roots of c, so n = 2. The number of roots is equal to n, so there are two square roots of c, named p0 and p1. The modulus of the roots is equal to the square root of r = 16, the modulus of c. Thus, p0 and p1 both have modulus .
The smaller the subscript of p, the smaller the argument of the root is. Therefore, p0 always represents the root with the smallest argument. To calculate the argument of p0, divide θ = 100° by n = 2.
You conclude that p0 is a square root of c; it has modulus 4 and argument 50°.
p0 = 4(cos 50° + isin 50°)
Note: In Problems 18.41–18.42, c = 16(cos 100° + isin 100°).
18.42 Calculate the remaining square root(s) of c.
As Problem 18.41 explains, c has two square roots: p0 and p1. Both have the same modulus, so p1 also has a modulus of 
To calculate the argument of the remaining root, first divide 360° by n = 2.
Add this value to the argument of p0, which is 50° according to Problem 18.41. That sum is the argument of p1.
You conclude that p1 = 4(cos 230° + isin 230°).
Note: In Problems 18.43–18.44, z = 8(cos 210° + isin 210°).
18.43 Determine how many cube roots exist for z and calculate the cube root with the smallest argument.
Exactly n = 3 cube roots exist for any complex number: p0, p1, and p2. You are asked to calculate p0, the cube root with the smallest argument.
Not all books name the roots the same way. Your book might use a different letter than p, but the process is the same.
Each of the roots has the same modulus: the cube root of the modulus of z.
The argument of p0 is equal to θ = 210° divided by n.
You conclude that p0 = 2(cos 70° + isin 70°).
Note: In Problems 18.43–18.44, z = 8(cos 210° + isin 210°).
18.44 Calculating the remaining cube roots of z.
In Problem 18.43, you determine that p0 = 2(cos 70° + isin 70°). The moduli of p1 and p2 are equal to the modulus of p0. To calculate the arguments of p1 and p2, you must first divide 360° by n = 3. The angles are evenly spaced at an interval of 360/n degrees around the unit circle.
Add 120° to the argument of p0 to calculate the argument of p1.
Add 120° to the argument of p1 to calculate the argument of p2.
Recall that both p1 and p2 have modulus 2; their arguments are 190° and 310°, respectively.
18.45 Calculate the fifth roots of 
You are directed to calculate all of the fifth roots of complex number c. There are n = 5 fifth roots, named p0, p1, p2, p3, and p4. Each of the roots has the same modulus.
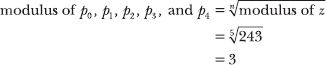
To calculate the argument of p0, divide θ = π/3 by n = 5.
Dividing by 5 is equivalent to multiplying by 1/5, the reciprocal of 5.
You now know the modulus and argument of p0, so you can express the complex number in trigonometric form.
The remaining roots have arguments that are equally spaced around the unit circle, at an interval of 2π/n.
This angle is measured in radians, so use the formula 
instead of 360°/n.
Add 2π/5 to the argument of p0 to calculate the argument of p1.
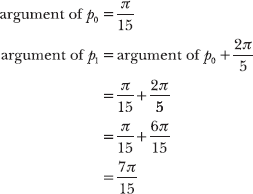
Add 2π/5 to the argument of p1 to calculate the argument of p2.
Add 2π/5 to the argument of p2 to calculate the argument of p3.
Finally, Add 2π/5 to the argument of p3 to calculate the argument of p4.
List all of the fifth roots, recalling that each has modulus 
