Graphs of Inverse Trigonometric Functions
Including domain and range
9.1 The graph of a function f(x) passes through points (–2,6), (0,3), and (4,–9) and has inverse function f–1(x). Identify three points through which the graph of f–1(x) passes.
If f(x) passes through points (–2,6), (0,3), and (4,–9), then –2, 0, and 4 are members of the domain and 6, 3, and –9 are members of the range. Specifically, f(–2) = 6, f(0) = 3, and f(4) = –9. To identify points on the inverse function f–1(x), reverse the numbers in the ordered pair.
If a number is a member of the domain, you can plug it into the function and get some real number output. Members of the range are outputs of the function.
Thus, f–1(x) passes through points (6,–2), (3,0), and (–9,4). In function notation, you conclude that f–1(6) = –2, f–1(3) = 0, and f–1(–9) = 4.
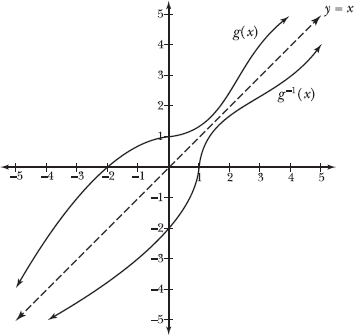
Note: Problems 9.2–9.4 refer to the graph of function g(x) below.

9.2 Explain how you can verify that g(x) is a function based on its graph and determine whether or not the function is one-to-one.
Every input x of the function may be paired with only one output g(x). To verify this on the graph of g(x), you apply a visual technique called the vertical line test. If a vertical line drawn on the coordinate plane intersects g(x), then that line represents an x-value in the domain of g(x). However, if any vertical line intersects the graph more than once, then g(x) fails the vertical line test and is not a function. No vertical line drawn on this graph intersects g(x) more than once, so you can visually verify that g(x) is a function.
If the vertical line x = 1 were to intersect g(x) at a height of 2 and a height of –3, then g(1) = 2 and g(1) = –3. See why that’s not allowed? The input x = 1 is paired with TWO outputs (2 and –3), but in a function, input values can only be paired with ONE output.
The horizontal line test is applied to the graph of a function to determine whether or not that function is “one-to-one.” In a one-to-one function, not only is each input paired with only one output, each output is paired with only one input. This graph passes the horizontal line test—no horizontal line intersects the graph more than once. Therefore, g(x) is one-to-one. Only one-to-one functions have inverses, so if a graph fails the horizontal line test, it does not have an inverse function.
Note: Problems 9.2–9.4 refer to the graph of g(x) in Problem 9.2.
9.3 Graph g –1(x), the inverse function of g(x).
Notice that g(x) passes through points (–5,–4), (–3,–1), (–2,0), (0,1), (3,4), and (4,5). Reverse the coordinates to identify points on the graph of inverse function g–1(x): (–4,–5), (–1,–3), (0,–2), (1,0), (4,3), and (5,4).

Note: Problems 9.2–9.4 refer to the graph of g(x) in Problem 9.2.
9.4 Explain how to transform the graph of g(x) to generate the graph of g–1(x).
As Problem 9.3 explains, the x- and y-coordinates of points on the graph of a function are reversed to identify points on the inverse function. For instance, if the graph of a one-to-one function g(x) passes through point (a,b), then the graph of its inverse function g–1(x) passes through (b,a).
Reversing the coordinates produces a reflection of the original graph across the line y = x, which passes through the origin and forms 45° (π/4 radians) angles with the positive x- and y-axes. Consider the following diagram, in which function g(x) and its inverse g –1(x) mirror each other across the dotted linear graph of y = x.
9.5 Explain why f(x) = cos x does not have an inverse function if its domain is all real numbers but does have an inverse if you restrict the domain to the interval 0 ≤ θ ≤ π.
Any horizontal line that intersects the graph of f(x) = cos x intersects it infinitely many times. As an example, consider the horizontal line f(x) = 0, the x-axis, which intersects the graph at x = (kπ)/2, where k is an odd integer. According to the horizontal line test, if any horizontal line intersects the graph more than once (let alone infinitely many times), that graph is not one-to-one and thus does not have an inverse.

However, you can define an inverse function for cosine if you restrict its domain to a small portion of the graph. In the diagram below, a specific interval of the graph of f(x) = cos x is highlighted. That portion (lying between x = 0 and x = π) passes the horizontal line test and is, therefore, one-to-one.

As Problem 9.5 explains, the function f(x) = cos x has an inverse function if you restrict the domain of f(x) to 0 ≤ x ≤ π. The inverse of the cosine function is arccosine and is written “arccos x.” Some textbooks (and many calculators) use the notation “cos–1 x” to represent the inverse cosine function, but this notation is not recommended. Recall that cos2x = (cos x)2, so cos–1x is easily confused with (cos x)–1, the reciprocal of cosine rather than the inverse of cosine.
Consider the darkened portion of the graph in Problem 9.5. It passes through key points (0,1), (π/2,0), and (π,–1). Reverse the coordinates to identify points on the graph of f–1(x) = arccos x: (1,0), (0,π/2), and (–1,π).

9.7 Identify the domain of arccos x.
Any vertical line that intersects a graph represents an element of that function’s domain. Consider the graph of arccos x generated in Problem 9.6. The vertical lines x = –1 and x = 1 intersect the graph, and so do all of the vertical lines between those x-values. Therefore, the domain of arccos x is –1 ≤ x ≤ 1.
This makes sense. Cosine outputs values between –1 and 1, so the INPUTS of arccosine are between –1 and 1. The outputs of a function are the inputs of its inverse and vice versa.
9.8 Identify the range of arccos x.
Horizontal lines drawn on the coordinate plane intersect the graph of arccos x at a lower bound of 0 and at an upper bound of π. Note that any horizontal line between those bounds also intersects the graph. Therefore, the range is 0 ≤ arccos x ≤ π.
9.9 Identify the restricted domain of sin x that has inverse arcsin x.
As illustrated in the following graph, the portion of sin x lying between x = –π/2 and x = π/2 passes the horizontal line test and is one-to-one. The inverse function arcsin x is defined for only that portion of the graph.
9.10 Graph arcsin x.
Note that the darkened portion of the graph in Problem 9.9 passes through key points (–π/2,–1), (0,0), and (π/2, 1). Therefore, the inverse function passes through points (–1,–π/2), (0,0), and (1,π/2), as illustrated below.

9.11 Identify the domain and range of arcsin x.
Consider the graph of y = arcsin x, presented in Problem 9.10. Vertical lines drawn on the coordinate plane intersect the graph at x = –1, x= 1, and at all of the x-values between them. Therefore, the domain of arcsin x is –1 ≤ x ≤ 1.
Notice that the domain of arcsin x matches the domain of arccos x (calculated in Problem 9.7); both are equal to the ranges of the inverse functions, in this case sin x. The range of arcsin x is equal to the restricted domain defined in Problem 9.9: –π/2 ≤ arcsin x ≤ π/2.
9.12 Identify the restricted domain of tan x that has inverse arctan x.
One full period of y = tan x lies between vertical asymptotes x = –π/2 and x = π/2. If you restrict tangent to this interval of the domain, you can define inverse function arctan x. Thus, the restricted domain of tangent is –π/2 < x < π/2. This is similar to the restricted domain of sine (defined in Problem 9.9) but it excludes the upper and lower bounds.
The graph of f(x) = tan x passes through points (–π/4, –1), (0,0), and (π/4, 1). Thus, the graph of f–1(x) = arctan x passes through points (–1,–π/4), (0,0), and (1,π/4), as illustrated in the following graph.

9.14 Identify the domain and range of y = arctan x.
The graph of y = arctan x, presented in Problem 9.13, is defined for all real numbers; any vertical line drawn on the coordinate plane intersects the graph. The range of the function is equal to the restricted domain of tan x (identified in Problem 9.13): –π/2 < arctan x < π/2.
Notice that the boundaries of the range are not included—unlike the boundaries of the ranges of arccos x and arcsin x—because the graph of arctan x is bounded above and below by horizontal asymptotes.