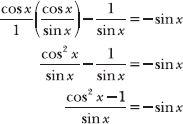Pythagorean Identities
For example, cos2 x + sin2 x = 1
7.23 List the three Pythagorean identities, in terms of θ.
Each of the three Pythagorean identities is an equation that contains two squared trigonometric functions, a sum, and the real number 1.
- cos2 θ + sin2 θ = 1
- 1 + tan2 θ = sec2 θ
- 1 + cot2 θ = csc2 θ
Note that θ, x, or any other variable may be used in the identities; the choice of variable does not affect the validity of the statement. For example, the first identity written in terms of x is equally valid: cos2 x + sin2 x = 1.
According to Problem 7.23, cos2 θ + sin2 θ = 1. Substitute θ = π/4 into each of the trigonometric functions and square the values to verify that the equation is true.
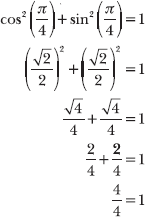
![]() means the same thing as
means the same thing as ![]() . Plug in
. Plug in ![]() to get
to get ![]() and then square that.
and then square that.
Any non-zero real number divided by itself equals 1. In this case, 4/4 = 1, so the statement is true.
7.25 Verify that the Pythagorean identity relating secant and tangent is true for θ = π/6.
Substitute θ = π/6 into the Pythagorean identity 1 + tan2 θ = sec2 θ and verify that the resulting statement is true.

Multiply the entire equation by 3/4 to eliminate the fraction in the denominators.

Recall that cos2 x + sin2 x = 1. If you subtract sin2 x from both sides of that identity, you produce the equally valid identity cos2 x = 1 – sin2 x. Therefore, you can replace 1 – sin2 x in the numerator of this expression with cos2 x.

Dividing by sec x is the same thing as multiplying by its reciprocal, cos x. This works just like Problem 7.7, where dividing by cosecant is the same as multiplying by sine.
7.27 Simplify the expression: ![]() .
.
According to a Pythagorean identity, 1 + tan2 θ = sec2 θ. If you subtract 1 from both sides of that equation, you produce the equally valid identity tan2 θ = sec2 θ – 1. Use this identity to rewrite the numerator of the fraction and simplify.

7.28 Simplify the expression: ![]() .
.
Factor sin x out of each term in the numerator, and factor cos x out of each term in the denominator.
If you need to review factoring, look at Chapter 12 in The Humongous Book of Algebra Problems.
![]()
If you subtract cos2 x and 1 from both sides of the expression cos2 x + sin2 x = 1, the result is sin2 x – 1 = –cos2 x.
![]()
If you subtract cos2 x from both sides of the Pythagorean identity cos2 x + sin2 x = 1, the result is sin2 x = 1 – cos2 x. Use this equation to rewrite the parenthetical quantity in the denominator. Then, simplify the fraction.

Factor the difference of perfect squares on the left side of the equation.
(csc2 θ – cot2 θ) (csc2 θ + cot2 θ) = 2csc2 θ – 1
Recall that 1 + cot2 θ = csc2 θ. If you subtract cot2 θ from both sides of that Pythagorean identity, the result is 1 = csc2 θ – cot2 θ. Use this statement to simplify the left side of the equation.
(1) (csc2 θ + cot2 θ) = 2csc2 θ – 1
Add and subtract like terms to simplify the expression.

Subtract ![]() from both sides, then add 1 to both sides. You end up with a Pythagorean identity, so you’re done.
from both sides, then add 1 to both sides. You end up with a Pythagorean identity, so you’re done.
7.30 Simplify the expression: ![]() .
.
In order to add the fractions, you need to express them in terms of the least common denominator (1 – sin x)(1 + sin x).

Combine like terms in the numerator and multiply the factors in the denominator.

Note that 1 – sin2 x = cos2 x, as explained in Problem 7.26.

7.31 Verify the statement: ![]() .
.
Expand the left side of the equation, and rewrite the single fraction on the right side of the equation as the sum of two fractions with common denominator cos2 θ.
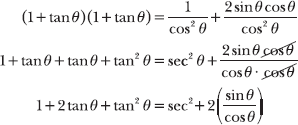
According to a Pythagorean identity, 1 + tan2 θ = sec2 θ.
Both sides of the equation are equal, so the original statement is verified.

7.32 Verify the identity: ![]() .
.
This equation is a proportion, so you can cross-multiply to eliminate the fractions.
Like most of the problems in this chapter, there are different ways to verify the statement. For example, you could rewrite cos2 x as (1 – sin2 x) and then factor that as (1 + sin x) (1 – sin x). Then, you can simplify the fraction on the right side of the equation, eliminating (1 + sin x) from the numerator and denominator.

Combine the fractions on the left side of the equation and apply the Pythagorean identity cos2 x + sin2 x = 1, rewritten as 1 – sin2 x = cos x.
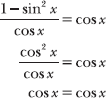
7.33 Verify the statement: ![]() .
.
Dividing by tan x is equivalent to multiplying by its reciprocal, cot x.

Rewrite the trigonometric functions in terms of sine and cosine and simplify.
Note that cos2 x – 1 = –sin2 x.