Eliminating squares instead of factoring them
Note: In Problems 11.1–11.2, you solve the equation tan2 x – 1 = 0 using two different techniques. Report the solutions on the interval 0 ≤ x < 2π.
11.1 Solve the equation by factoring the expression tan2 x – 1.
The expression tan2 x – 1 is a difference of perfect squares. Factor it and apply the zero-product property, setting each of the individual factors equal to zero and solving those equations.
If you need to review this technique, check out Problems 10.12–10.23.
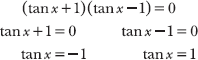
The solutions to the equation tan2 x – 1 = 0 are the angles x on the interval 0 ≤ x < 2π that have a tangent of –1 or +1.
Note: In Problems 11.1–11.2, you solve the equation tan2 x – 1 = 0 using two different techniques. Report the solutions on the interval 0 ≤ x < 2π.
11.2 Solve the equation using square roots to verify your solution to Problem 11.1.
Unlike the factoring and quadratic formula techniques for solving quadratic equations, applying square roots does not require that one side of the equation be equal to 0. Begin by adding 1 to both sides.
tan2 x = 1
Take the square root of both sides of the equation. Note that any even root applied to both sides of an equation requires the insertion of a “±” symbol.
For example, to solve the equation x2 = 16, you take the square root of both sides to get x = ±4. There are two answers, because +4 and –4 both equal 16 when squared.
Thus, the solutions to the equation are all angles x on the interval 0 ≤ x < 2π that have a tangent value of either –1 or +1. This is the same set of angles identified in the solution to Problem 11.1.
11.3 Identify the solutions to the equation 4 sin2 x – 4 sin x + 1 = 0 on the interval 0 ≤ x < 2π.
Factor the quadratic expression left of the equal sign. Note that the quadratic formula will also produce the correct solution to this equation, but it requires more arithmetic than the technique described in this solution.
(2 sin x – 1) (2 sin x – 1) = 0
Note that the factors are equal, so the left side of the expression can be expressed as a square.
(2 sin x – 1)2 = 0
Take the square root of both sides of the equation. Note that the “±” may be omitted because ±0 = 0.
Two angles on the interval 0 ≤ x < 2π have a sine value of 1/2.
11.4 Identify the solutions to the equation 2(cos2 x + 4) – 9 = 0 on the interval 0 ≤ x < 2π.
Simplify the expression left of the equal sign and then take the square root of both sides.
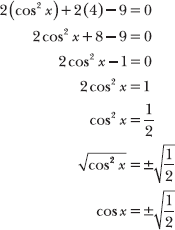
Rationalize the denominator on the right side of the expression to reveal a familiar value of cosine.
There are four angles on the interval 0 ≤ x < 2π that have a cosine value of 
.
11.5 Identify the solutions to the equation 3 csc2 2x = 4 on the interval 0 ≤ x < 2π.
Isolate csc2 2x on the left side of the equation and then take the square root of both sides.
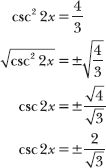
Apply a reciprocal identity to express cosecant in terms of sine. Then apply the arcsine function to eliminate sine from the left side of the equation.
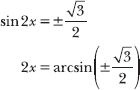
You use arcsine to get rid of sine and leave behind the 2x that was plugged into it. The equation’s not solved until you divide by 2 at the end and solve for x.
The four angles on the interval 0 ≤ x < 2π that have a sine of 
are π/3, 2π/3, 4π/3, and 5π/3. However, because x has a coefficient of 2, you should list twice as many solutions. Add 2π to each of those four solutions to generate the list of eight solutions below.
If the coefficient of x is N, then you have to list N times the number of answers you normally would. (See Problem 10.34.) This is only true when you are identifying solutions on a specific interval like 0≤ x < 2Π
Multiply each of the values by 1/2 to solve for x.
11.6 Identify the solutions to the equation 9 cot4 x – 1 = 0 on the interval 0 ≤ x < 2π.
Factor the difference of perfect squares and apply the zero-product property.
Note that the equation cot2 x = –1/3 has no solution, because no squared value can be equal to a negative number. Solve the remaining equation by taking the square root of both sides.
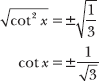
It is helpful to divide the numerator and denominator of the fraction by 2 and express cot x in terms of cosine and sine.
There are four angles with cosine values of ±1/2 and sine values of ±√3/2.
