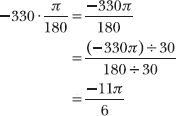Converting Between Angle Measurements

Especially degrees and radians

In order to convert from one unit of angle measurement to another, you multiply it by a fraction of the following form:

Select a simple angle when you create the fraction. For example, Problems 1.9–1.10 state that 1 revolution = 360°. This problem instructs you to convert from revolutions to degrees, so “an angle measured in the new units” would be 360°, and “the same angle measured in the old units” would be 1 revolution. Note that the units themselves are omitted from the fraction:

Thus, to convert 3 revolutions into degrees, you multiply by 360/1, or more simply, 360.

You conclude that an angle measurement of 3 revolutions is equivalent to an angle measurement of 1,080°.

According to Problem 1.20, to convert from one unit of measurement to another, you multiply by the fraction whose numerator is an angle expressed in the new units to which you are converting and whose denominator is the same angle expressed in the old units from which you are converting. In this case, you are converting from degrees to revolutions, so the new units are revolutions and the old units are degrees.

Once again, it is appropriate to select a simple angle for the equal measurements. Apply the equivalency relationship 1 revolution = 360°, like you did in Problem 1.20.

Multiply 210° by the conversion fraction identified above.

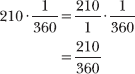
Reduce the fraction to lowest terms by dividing its numerator and denominator by the greatest common factor of 210 and 360, which is 30.

Can’t remember how to reduce fractions? Check out Problems 7.27–7.34 in The Humongous Book of Basic Math and Pre-Algebra Problems.

Therefore, 210° is equal to , or revolutions.

That little bar over the 3 means that the digit repeats infinitely: 0.5833333333333….

As Problems 1.20–1.21 demonstrate, to convert from one unit of angle measurement to another, you need to identify a fraction with values representing the same angle in the old and new units. In this problem, you are converting from revolutions to radians, so the new units are radians and the old units are revolutions. Because radians are typically expressed as fractions, rather than decimals, you should rewrite 0.5 as a fraction:

Like Problems 1.20–1.21, you can use the measure of 1 full revolution about the coordinate plane to create the necessary conversion fraction: 1 revolution = 2π radians.

Therefore, to convert 1/2 revolutions into radians, multiply by 2π.

Crossing out these common factors in the numerator and denominator is just a quick way to say, “I divided both of these things by 2 to reduce the fraction.”

Apply the same angle measurements that you used in Problem 1.22 (1 revolution = 2π radians). In this problem, however, the new units are revolutions and the old units are radians.

Multiply 7π/4 by the conversion fraction above.

Reduce the product to lowest terms, dividing the numerator and the denominator by the greatest common factor (π).

You conclude that 7π/4 radians = 7/8 revolutions.

Like the preceding problems in this section, you must create a conversion fraction whose numerator and denominator are measures of the same angle in the new and old units, respectively. In this problem, the new units are radians and the old units are degrees. According to Problems 1.10–1.11, 1 full revolution measures 2π radians and 360°.

This fraction should be reduced to lowest terms, because the numerator and denominator are both divisible by 2.

Therefore, you should multiply an angle measurement by π/180 to convert it from degrees to radians.

And, as you’ll see in Problems 1.27–1.30, you multiply by to convert from radians to degrees.

Reduce the fraction to lowest terms.

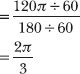
Therefore, 120° = 2π/3 radians.

As Problem 1.24 explains, to convert an angle measurement from degrees to radians, multiply it by π/180 and (when possible) reduce the resulting fraction to lowest terms.

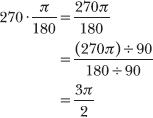
You conclude that 270° = 3π/2 radians.

The sign of an angle measurement does not affect the technique you apply to convert between different units. Therefore, you should apply the same technique modeled in Problems 1.24–1.25: Multiply the angle measurement by π/180. Note that the radian angle measurement must have the same sign as the degree angle measurement, so your final answer will be negative.

You conclude that –330° radians.

According to this, the numerator is negative. If a fraction has a negative numerator or denominator, the negative sign is usually written in front of the fraction, like this.

To convert from radians to degrees, multiply the radian angle measurement by 180/π and reduce the resulting fraction to lowest terms.

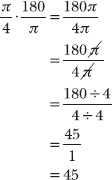
Therefore, π/4 radians = 45°. Because most radian measurements contain π, they are easily differentiated from degree measurements. (Degree measurements always include the degree symbol, as well.) Therefore, the word “radians” is usually omitted when reporting an angle measurement. In trigonometry, if no units are written next to an angle, you should assume that the angle is measured in radians. Hence, it is more common to write the answer to this problem as π/4 = 45°.

So you don’t have to write “radians” next to radian measurements to specify the units.

Apply the same procedure demonstrated in Problem 1.27: Multiply the radian angle measurement by 180/π. Note that an angle with a negative radian measure will also have a negative degree measure.

Before you multiply 5 and 180 in the numerator of the product, reduce the numerator value 180 and the denominator value 6, which share a greatest common factor of 6.

You conclude that –5π/6 = –150°.

One revolution is equal to 2π. Calculate the value equivalent to 2π that has a denominator of 4, by multiplying the numerator and denominator of 2π/1 by 4.

Because 15π/4 > 8π/4, you know that 15π/4 is larger than 1 revolution. This does not affect the technique you use to convert the angle measurement—you still multiply by 180/π, but you should expect a degree measurement larger than 360°.

Note that 180 and 4 share a greatest common factor of 4. Eliminate it to reduce the fraction.

All of the other radian measurements so far have had π in them somewhere, which makes an angle of 2 radians feel weird. Not to worry—you still multiply by to convert it into degrees.

As Problem 1.27 explains, any angle measurement written without units is assumed to be expressed in radians. Therefore, this problem instructs you to convert 2 radians into degrees.

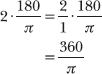
You conclude that 2 radians = (360/π)°, which is approximately equal to 114.592°.