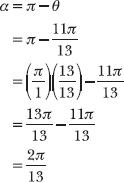Shrink rays that turn any angles into acute angles
4.1 Given acute angle θ in the diagram below, draw reference angles in the second, third, and fourth quadrants that have the same measure as θ.
A reference angle is an acute angle formed by a terminal side and the x-axis. Reference angles are not necessary in the first quadrant, but each of the other quadrants requires them. The diagram below illustrates the reference angles for the second, third, and fourth quadrants, each with an angle measure of θ.
Even though the size of θ may change, all reference angles are acute. All four together resemble a bowtie with a knot at the origin. Whenever you draw a reference angle, it will look like one of these four pieces of bowtie.
Note: Problems 4.2–4.5 refer to angle α in the diagram below.
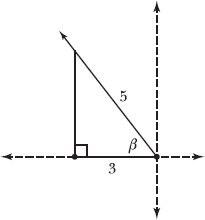
4.2 Draw β, the reference angle for α.
The terminal side of α lies in the second quadrant. Recall that a reference angle is formed by the terminal side of an angle and the x-axis, in this case the negative x-axis. In the diagram below, β is the reference angle for α.
Note: Problems 4.2–4.5 refer to the diagram in Problem 4.2. Note that β is the reference angle for α.
4.3 Given 
, calculate sin α.
The sine function is defined in terms of a right triangle, equal to the length of the leg opposite an angle divided by the length of the hypotenuse. Draw a vertical line segment extending from the terminal side of β to the negative x-axis, forming a right triangle as demonstrated in the following diagram. Because sin β = 4/5, the length of the vertical segment (the leg opposite β) is 4, and the length of the hypotenuse is 5.
You may be wondering why the x- and y-axes are dotted in this diagram. Forget, for the moment, that β is in the second quadrant. It is a reference angle, and is therefore not required to be in standard position. You can treat the right triangle as you would any triangle not confined to a coordinate plane. Its lengths are positive.
The purpose of a reference angle is to provide the values you need for the original angle. Only when you refer to the actual angle do you need to concern yourself with the quadrants of the coordinate plane and the signs of the functions.
Because sin β = 4/5, and β is the reference angle for α, you can conclude that sin α = ±4/5. Angles and their reference angles have trigonometric values that are either equal or are opposites.
This is very important.
Now it is time to calculate the sine value of α, the original angle.
In the second quadrant, where angles α and β terminate, you travel left and up from the origin. Therefore, x-values are negative and y-values are positive. The side opposite β (the reference angle) has a signed length of +4, because you travel upward from the x-axis to reach the terminal side. The hypotenuse is always considered a positive value.
Therefore, sin α = 4/5, which is exactly equal to the given value, sin β.
Note: Problems 4.2–4.5 refer to the diagram in Problem 4.2. Note that β is the reference angle for α.
4.4 Given 
, calculate cos α.
In Problem 4.3, you draw a vertical segment from the terminal side to the x-axis in order to create a right triangle. You can use that triangle again in this problem. Because cos β = 3/5 (and cosine is the quotient of the adjacent leg and the hypotenuse), the length of the adjacent leg is 3 and the length of the hypotenuse is 5.
The length of the opposite side is still 4, but that’s not needed in this problem.
Recall that the trigonometric values of an angle and its reference angle are either equal or opposites, so cos β = 3/5. You determine the sign of 3/5 when you consider the quadrant in which the terminal side of α and β lie.
The terminal sides of α and β lie in the second quadrant. As a result, the side adjacent to β (which is horizontal) extends left of the origin. Therefore, it has a negative signed length. Remember that the length of the hypotenuse is always considered positive.
Here’s a quick guide to signed lengths for each quadrant:
I: horizontal and vertical: +
II: horizontal = –, vertical = +
III: horizontal and vertical: –
IV: horizontal = +, vertical = –
Seem familiar? They are also the signs of the x- and y-coordinates for each quadrant.
You conclude that cos α is the opposite of cos β.
Note: Problems 4.2–4.5 refer to the diagram in Problem 4.2. Note that β is the reference angle for α.
4.5 Given tan 
, calculate tan α.
Begin this problem in the same way you began Problems 4.3–4.4, drawing a vertical line from the terminal side toward the x-axis to form a right triangle.
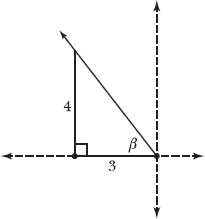
Angle α (and its reference angle β) terminate in the second quadrant, where horizontal signed lengths are negative and vertical signed lengths are positive.
Note: Problems 4.6–4.7 refer to the diagram below, in which θ is an angle in standard position that measures 135°.
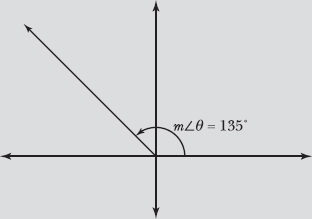
4.6 Draw α, the reference angle for θ, and calculate 
in degrees.
The reference angle for θ is formed by the negative x-axis and the terminal side of θ, as illustrated below.
Notice that θ and α are supplementary—together they form a straight angle whose initial side is the positive x-axis and whose terminal side is the negative x-axis. Therefore, the sum of their measures is 180°.
Substitute 
into the equation and solve for 
.
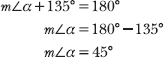
Note: Problems 4.6–4.7 refer to the diagram in Problem 4.6, in which θ is an angle in standard position that measures 135°.
4.7 Generalize your solution to Problem 4.6 in order to create a formula that computes the reference angle α for any angle θ in standard position, such that 
. Construct the equivalent formula for angles measured in radians, as well.
You have to specify that the angle is between 90° and 180° for this formula to work, because all kinds of angles terminate in the second quadrant. For example, a 495° angle in standard position also terminates in the second quadrant, and 180° – 495° = – 315° is definitely NOT its reference angle.
In Problem 4.6, you recognize that an angle in standard position terminating in the second quadrant has a supplementary reference angle. Therefore, the measure of the reference angle is the difference of 180° and the original angle. In Problem 4.6, angle θ in standard position has a measure of 135°, and its reference angle α has measure 180° – 135°, as illustrated below.
Given any angle θ in standard position such that 
, you can conclude (A) the angle terminates in the second quadrant, and (B) the measure of its reference angle is equal to the difference of 180° and 
.
If angle θ is measured in radians, the measure of its reference angle α is computed according to the following formula.
These formulas are equivalent because 
.
Note: Problems 4.8–4.9 refer to an angle θ in standard position and its reference angle α. Note that 
.
4.8 Draw angles α and θ in the coordinate plane and calculate the measure of α in degrees.
Angle θ measures 250°. An angle in standard position that terminates at the negative y-axis has a measure of 270°. Therefore, the terminal side of θ lies 270° – 250° = 20° clockwise from the negative y-axis, as illustrated in the following diagram. Reference angle α is formed by the terminal side of θ and the negative x-axis. Unlike the angle/reference angle pair examined in Problems 4.6–4.7, θ and its reference angle overlap.
Notice that θ passes through quadrants I and II before it overlaps angle α in the third quadrant. Therefore, to calculate the measure of α, you subtract the measure of the angle whose initial side is the positive x-axis and whose terminal side is the negative x-axis.
According to Problem 4.6, the angle containing the first two quadrants measures 180°.
Note: Problems 4.8–4.9 refer to an angle θ in standard position and its reference angle α. Note that 
.
4.9 Generalize your solution to Problem 4.8 in order to create a formula that computes the reference angle α for any angle θ in standard position, such that 
. Construct the equivalent formula for angles measured in radians, as well.
Any angle whose measure falls between 180° and 270° has a terminal side that lies in the third quadrant. As Problem 4.8 demonstrates, the angle θ and its reference angle α overlap in the third quadrant. Therefore, the measure of reference angle α is exactly 180° less than the measure of angle θ.
To calculate the measure of reference angle α in radians, express 180° as π.
Note: Problems 4.10–4.11 refer to an angle θ in standard position and its reference angle α. Note that 
.
4.10 Draw angles α and θ in the coordinate plane and calculate the measure of α in radians.
Angle θ terminates in the fourth quadrant. (You may wish to convert the angle to degrees if you have trouble visualizing radian angle measurements.) Its reference angle α is formed by the terminal side of θ and the positive x-axis, as illustrated below.
Notice that angles θ and α, when combined, form 1 full rotation in the coordinate plane. Therefore, the sum of their measures is 2π (or 360°).
You are given 
. Substitute this value into the equation and solve for 
.
Express both terms using the least common denominator 3 and simplify the expression.
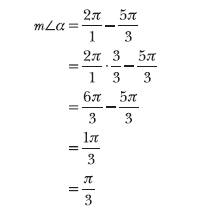
Note: Problems 4.10–4.11 refer to an angle θ in standard position and its reference angle α. Note that 
.
4.11 Generalize your solution to Problem 4.10 in order to create a formula that computes the reference angle α for any angle θ in standard position, such that . Construct the equivalent formula for angles measured in degrees, as well.
As Problem 4.10 demonstrates, the measure of reference angle α is equal to the difference of 2π and 
. To express this formula in degrees, convert 2π into 360°.
4.12 Given angle θ in standard form that measures 165°, calculate the measure of its reference angle α.
Because 90° < 165° < 180°, the terminal side of θ lies in the second quadrant. According to Problem 4.7, the measure of reference angle α for a second-quadrant angle θ is computed according to the following formula.
Substitute the given measure of θ into the equation to calculate the measure of reference angle α.
4.13 Given angle θ in standard form that measures 321°, calculate the measure of its reference angle α.
Because 270° < 321° < 360°, the terminal side of θ lies in the fourth quadrant. According to Problem 4.11, the measure of reference angle α for a fourth-quadrant angle θ is computed according to the following formula.
Substitute the given measure of θ into the equation to calculate the measure of reference angle α.
, calculate the measure of its reference angle α.Note that the terminal side of θ lies in the third quadrant, because π < 7π/6 < 3π/2. According to Problem 4.9, the measure of reference angle α for a third-quadrant angle θ is computed according to the following formula.
Problem 3.34 explains how to figure out where an angle’s terminal side lies. In fact, it uses this exact angle as an example. Make sure you understand this trick before you move on to Problem 4.15.
Substitute the given measure of θ into the equation to calculate the measure of reference angle α.
4.15 Given angle θ in standard form that measures 
, calculate the measure of its reference angle α.
The quotient of the numerator and denominator (excluding π) is equal to 
, so the terminal side of θ lies in the second quadrant. Apply the appropriate reference angle formula to calculate the measure of reference angle α.
The book is using the trick from Problem 3.34.
