Perpendicular vectors
16.31 Describe the geometric relationship between orthogonal vectors.
Orthogonal vectors are perpendicular to each other. Therefore, intersecting orthogonal vectors intersect at right angles.
Note: In Problems 16.32–16.36, you explore four different techniques to verify that vectors u = <3, 3> and v = <5, –5> are orthogonal.
16.32 Plot u and v, and use their direction angles to verify that the vectors are orthogonal.
Plot u and v in the coordinate plane. You will measure the angle between them by calculating the angles each vector forms with the positive x-axis.
Apply the technique demonstrated in Problem 16.19 to calculate the direction angle θ of vector u—the measure of the angle formed by u and the positive x-axis.
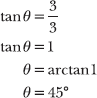
Similarly, the angle between v and the positive x-axis measures 45°. The angle between u and v is the sum of those angles: 45° + 45° = 90°. Lines—and vectors—that intersect at 90° angles are perpendicular, so u and v are orthogonal.
Note: In Problems 16.32–16.36, you explore four different techniques to verify that vectors u = <3, 3> and v = <5, –5> are orthogonal.
16.33 Calculate the slopes of the lines that coincide with u and v, and use them to verify that the vectors are orthogonal.
“Coincide with” means “overlap.”
The slope of a vector in component form—and the slope of the line that coincides with that vector—is equal to the y-component of the vector divided by the x-component. Therefore, the slope of the line that coincides with u is 3/3 = 1. The slope of the line that coincides with v is –5/5 = –1.
Perpendicular lines have slopes that are negative reciprocals of each other. Because 1 and –1 are negative reciprocals, they represent the slopes of perpendicular lines. You conclude that u and v are orthogonal.
Note: In Problems 16.32–16.36, you explore four different techniques to verify that vectors u = <3, 3> and v = <5, –5> are orthogonal.
16.34 Apply the standard dot product formula to verify that u and v are orthogonal.
According to the standard dot product formula, <a, b> · <c, d> = ac + bd.
You conclude that u and v are orthogonal because they have a dot product of 0. In fact, any pair of nonzero vectors that have a dot product of 0 are orthogonal.
And vice versa: If vectors are orthogonal, they always have a dot product of 0. This only works for NONZERO vectors. The next problem explains why.
Note: In Problems 16.32–16.36, you explore four different techniques to verify that vectors u = <3, 3> and v = <5, –5> are orthogonal.
16.35 Determine whether u and w = <0, 0> are orthogonal vectors, and explain your answer.
If you calculate the dot product of u and w, the result is 0.
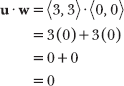
In fact, the dot product of any vector and the zero vector <0, 0> is equal to 0. However, you cannot conclude that u and w are orthogonal based upon the dot product value alone. Recall that orthogonal vectors are perpendicular, so the angle formed by the vectors should equal 90°.
Solve the alternate dot product formula for cos θ to better understand why u and w do not form a 90° angle.
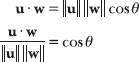
Some textbooks (and teachers) prefer this version of the formula.
Calculate the magnitudes of u and w.
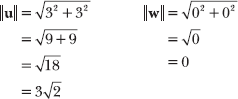
Substitute the dot product and vector magnitudes into the modified dot product formula.
Dividing by 0 is prohibited. Because you cannot calculate θ, you cannot conclude that θ is a right angle. Therefore, u and w are not orthogonal.
Note: In Problems 16.32–16.36, you explore four different techniques to verify that vectors u = <3, 3> and v = <5, –5> are orthogonal.
16.36 Calculate the angle between u and v to verify that the vectors are orthogonal.
Recall that u · v = 0, and according to Problem 16.35, 
. Calculate the magnitude of v.
Apply the modified dot product formula introduced in Problem 16.35 to compute the angle θ between u and v.
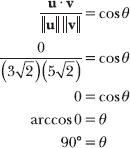
Vectors u and v form a 90° angle, so they are orthogonal.
16.37 Determine whether the vectors <2, –3> and <6, 4> are orthogonal.
Calculate the dot product of the vectors.
Because their dot product is equal to 0, vectors <2, –3> and <6, 4> are orthogonal.
16.38 Given A = (8, –2), B = (6, 1), C = (–3, –7), and D = (4, –4), determine whether 
and 
are orthogonal.
Subtract corresponding coordinates to express the vectors in component form.
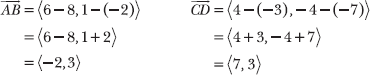
Calculate the dot product of the vectors.
Vectors 
and 
are not orthogonal because their dot product is not equal to 0.
If a and b are orthogonal vectors, then a · b = 0. Compute the dot product and set it equal to 0.
Solve the equation for c.
16.40 Given A = (3, 4), B = (12, –10), and z = <5c, –2>, calculate the value of c for which and z are orthogonal.
Express in component form.
Because the vectors are orthogonal, you can set their dot product equal to 0.
Solve for c.
