Looks like multiplication, but it’s not
16.1 Given v = <a, b> and w = <c, d>, explain how to calculate the dot product v · w.
To calculate the dot product of two vectors, add the product of their x-components to the product of their y-components.
v · w = ac + bd
Even though the dot here looks like multiplication, it stands for the “dot product.”
Note: In Problems 16.2–16.4, v = <1, 4> and w = <5, 2>.
16.2 Calculate v · w.
Apply the formula presented in Problem 16.1, which adds the products of the x-components and the y-components.
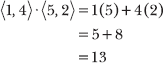
Note: In Problems 16.2–16.4, v = <1, 4> and w = <5, 2>.
16.3 Calculate 3v · w.
Before you apply the dot product, multiply v by the scalar 3.

Now apply the dot product formula.

You conclude that 3v · w = 39.
Multiply both components of v by 2, multiply both components of w by –3, and then compute the dot product.

Note: In Problems 16.5–16.6, you verify that the dot product is commutative using the vectors r = <–3, 7> and s = <–2, 10>.
In other words, r · s = s · r.
16.5 Calculate r · s.
Add the product of the x-components to the product of the y-components.

Note: In Problems 16.5–16.6, you verify that the dot product is commutative using the vectors r = <–3, 7> and s = <–2, 10>.
16.6 Calculate s · r.
According to Problem 16.5, r · s = 76. If the dot product is commutative, then s · r will also equal 76.

The order in which you list the vectors does not affect the value of the dot product—you still add the products of the x-components to the products of the y-components, and the result is the same. Therefore, the dot product is commutative.
Only the order of the components changes: –2(–3) instead of –3(–2), 10(7) instead of 7(10). Because multiplication is commutative, the order doesn’t affect the products.
Note: In Problems 16.7–16.8, you verify that the dot product of a vector with itself is equal to the square of the vector’s magnitude.
16.7 Given v = <–4, 6>, verify that ![]()
In this problem, you demonstrate that the relationship ![]() is true for the specific vector v = <–4, 6>; in Problem 16.8, you prove that the relationship is true for any vector.
is true for the specific vector v = <–4, 6>; in Problem 16.8, you prove that the relationship is true for any vector.
Calculate the dot product v · v on the left side of the equation, and apply the vector magnitude formula to calculate ![]() on the right side of the equation.
on the right side of the equation.
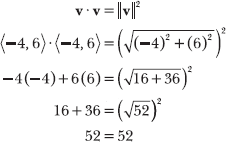
The square and square root cancel out, leaving 52 on the right side of the equation.
Note: In Problems 16.7–16.8, you verify that the dot product of a vector with itself is equal to the square of the vector’s magnitude.
16.8 Prove that ![]() for any general vector v = <a, b>.
for any general vector v = <a, b>.
Apply the same technique you used in Problem 16.7. In the solution below, note that the dot product v · v is equal to the expression inside the radical symbol.
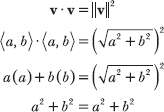
Note: In Problems 16.9–16.10, you use vectors u = <–3, 5>, v = <–4, 2>, and w = <–9, –1> to demonstrate that the dot product is distributive over addition: u · (v + w) = u · v + u · w.
16.9 Calculate u · (v + w).
In this problem, you calculate the dot product of u with the vector sum v + w. In Problem 16.10, you verify that this value is equal to the sum of the dot products u · v and u · w. In other words, the dot product can be distributed over a sum (or a difference). Begin by calculating v + w.


Note: In Problems 16.9–16.10, you use vectors u = <–3, 5>, v = <–4, 2>, and w = <–9, –1> to demonstrate that the dot product is distributive over addition: u · (v + w) = u · v + u · w.
16.10 Demonstrate that u · (v + w) = u · v + u · w.
According to Problem 16.9, u · (v + w) = 44. In this problem, you calculate the sum of the dot products u · v and u · w to verify that the dot product with a sum is equal to the sum of the dot products.

You conclude that u · (v + w) = u · v + u · w = 44.
16.11 Evaluate the expression: ![]() .
.
As Problems 16.9–16.10 demonstrate, the dot product is distributive over a vector sum. Thus, you can calculate the dot product of <3, 1/2> with each of the terms in parentheses and then calculate the sum.

Compute the sum using the least common denominator, 16.
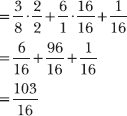
Note: In Problems 16.12–16.14, you use the vectors v = <7, 2> and w = <–4, 3> to investigate how scalar multiplication affects a dot product.
16.12 Demonstrate that 5(v · w) ≠ 5v · 5w.
As Problems 16.9–16.10 demonstrate, the dot product is distributive over a vector sum. However, scalar multiplication is not distributive over a dot product. In this problem, you verify that multiplying the dot product v · w by 5 is not equivalent to the dot product of 5v and 5w. Simplify both sides of the equation individually.

Note: In Problems 16.12–16.14, you use the vectors v = <7, 2> and w = <–4, 3> to investigate how scalar multiplication affects a dot product.
16.13 Demonstrate that 5(v · w) = 5v · w.
In Problem 16.12, you verify that scalar multiplication is not distributive over a dot product. However, multiplying a dot product of two vectors by a scalar is equivalent to the dot product of those vectors when exactly one of them—not both—is multiplied by the scalar. According to Problem 16.12, 5(v · w) = –110; in this problem you verify that 5v · w = –110 as well.
In other words, if you multiply ONE vector by the scalar and then calculate the dot product, you get the same answer as if you’d taken the dot product of the vectors first and then multiplied by the scalar.
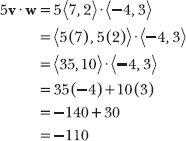
You conclude that 5(v · w) = 5v · w = –110.
Note: In Problems 16.12–16.14, you use the vectors v = <7, 2> and w = <–4, 3> to investigate how scalar multiplication affects a dot product.
16.14 Demonstrate that 5(v · w) = v · 5w.
In Problem 16.13, you verify that multiplying v by the scalar 5 and then computing the dot product with w is equivalent to multiplying the dot product v · w by the scalar 5. In this problem, you demonstrate that multiplying the other vector (w) by the scalar 5 has the same effect on the dot product. Recall that 5(v · w) = –110.
Thus, 5(v · w) = v · 5w = –110.
Moral of the story: If a dot product is multiplied by a scalar, you can multiply either one of the vectors by the scalar and then calculate the dot product to get the same result.
16.15 Evaluate the expression: ![]() .
.
You can either choose to calculate the dot product and then multiply by the scalar 2 or, as Problems 16.12–16.14 explain, multiply exactly one of the vectors by the scalar 2 and then compute the dot product. In the following solution, the vector <–2, 6> is multiplied by 2 and then the dot product is computed.

16.16 Evaluate the expression: ![]() .
.
In the following solution, the dot product is computed and the resulting value is multiplied by 1/3.


