Adding and Subtracting Graphically
Head-to-tail technique
15.1 Describe the technique used to add vectors graphically in the coordinate plane.
The sum of two vectors is also a vector, and it is a simple matter to visualize that sum in the coordinate plane through a technique known informally as the head-to-tail method. To add vector w to vector v, place the initial point of w at the terminal point of v. The sum v + w is called the resultant vector; it shares an initial point with v and a terminal point with w.
In other words, move w so it starts exactly where v ends.
15.2 Given v = <2,0>, calculate v + v by plotting the resultant vector in the coordinate plane.
Vector v = <2,0> is a horizontal vector with a magnitude of 2 and a direction angle of 0°; it points directly to the right, due east from its initial point. If you graph v in standard position, its initial point is (0,0) and its terminal point is (2,0).
In order to calculate v + v, graph v in standard position and then plot a second copy of v, such that the second vector begins where the first ends. As the following diagram illustrates, the second copy of v has an initial point of (2,0) and a terminal point of (4,0).
The resultant vector, illustrated in the following diagram, represents v + v. It begins at the initial point of the first vector (0,0) and ends at the terminal point of the second vector (4,0).
Note that the resultant vector is in standard position, because its initial point is the origin. Therefore, the coordinates of its terminal point are also its components: v + v = <4,0>.
15.3 Given r = <3,0> and s = <0,5>, calculate r + s by plotting the resultant vector in the coordinate plane.
Plot r in standard position; it has initial point (0,0) and terminal point (3,0). Next, plot s so that its initial point coincides with the terminal point of r. In other words, from its initial point (3,0), s travels a horizontal distance of 0 and a vertical distance of 5 units up.
Just pretend that (3,0)—the terminal point of r—is the origin, and plot s as you normally would.
The resultant vector r + s has initial point (0,0) and terminal point (3,5). Therefore, r + s = <3,5>.
Note: In Problems 15.4–15.5, v = <–4,–1> and w = <9,–2>.
15.4 Given v = <–4,–1> and w = <9,–2>, calculate v + w by plotting the resultant vector in the coordinate plane.
Plot v in standard position and then place the initial point of w at the terminal point of v.
The resultant vector has an initial point of (0,0) and a terminal point of (5,–3). Thus, v + w = <5,–3>.
Note: In Problems 15.4–15.5, v = <–4,–1> and w = <9,–2>.
15.5 Demonstrate that vector addition is commutative by plotting w + v in the coordinate plane and verifying that the resultant vector is equal to the sum calculated in Problem 15.4.
Commutative means the order in which you add doesn’t matter: v + w = w + v.
Plot w in standard position and then place the initial point of v at the terminal point of w.
The resultant vector has an initial point of (0,0) and a terminal point of (5,–3). Thus, w + v = <5,–3>.
15.6 Given A = (0,3), B = (4,2), C = (–1,–5), and D = (–7,1) calculate 
by plotting the resultant vector in the coordinate plane.
Express both of the vectors in component form by subtracting the components of their initial points from the components of their terminal points.
Plot 
in standard position. Its terminal point, (4,–1), is the initial point of 
.
Because 
you should travel 6 units left and 6 units up from (4, –1).
You conclude that 
15.7 Given r = <0,5> and s = <6,4>, calculate r – s by plotting the resultant vector in the coordinate plane.
In order to plot the resultant vector for vector subtraction, rewrite the subtraction expression using addition. In other words, rather than subtract s from r, you add –s to r. Multiply both components of s by –1 to calculate –s.
Plot r in standard position and then place the initial point of –s at the terminal point of r.
You conclude that r – s = <–6,1>.
Note: In Problems 15.8–15.9, v = –2i – j and w = 4i – 3j.
15.8 Calculate v + w by plotting the resultant vector in the coordinate plane.
Note that v and w are expressed in terms of standard unit vectors i = <1,0> and j = <0,1>. To rewrite each in component form, use the coefficients of i and j as the x- and y-components, respectively: v = <–2,–1> and w = <4,–3>. Plot v in standard position and then place the initial point of w on the terminal point of v, as illustrated in the following diagram.
The resultant vector, v + w, has component form <2,–4>.
Note: In Problems 15.8–15.9, v = –2i – j and w = 4i – 3j.
15.9 Calculate v – w by plotting the resultant vector in the coordinate plane.
According to Problem 15.8, v = <–2,–1> and w = <4,–3>. Multiply the components of w by –1 in order to generate the vector –w.
The vector sum v + (–w) is equivalent to the vector difference v – w. Plot v in standard position and then place the initial point of –w on the terminal point of v.
Just like 10 + (–5) = 10 – 5 = 5
You conclude that v – w = <–6,2>.
15.10 Given r = <3,2> and s = <1,–4>, calculate r – s by plotting the resultant vector in the coordinate plane.
Multiply the components of s by –1 to generate the vector –s.
The vector r – s is equivalent to the sum r + (–s).
You conclude that r – s = <2,6>.
Begin by multiplying the components of w by –1 to generate vector –w.
Plot u in standard position and place the initial point of v at the terminal point of u. Then, place the initial point of –w at the terminal point of v. The resultant vector stretches from the origin to (–5,2), as illustrated in the following diagram.
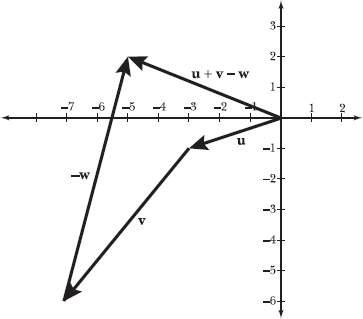
You conclude that u + v – w = <–5,2>.