Angles, front and center
Note: Problems 1.1–1.3 refer to the diagram below, triangle ABC.
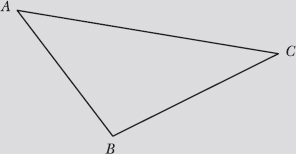
1.1 Identify the sides and vertices of the triangle.
A triangle is a two-dimensional (or plane) figure that consists of three line segments intersecting only at their endpoints. Line segments are named according to the points at which they begin and end, so the sides of this triangle are 
. The vertices are the three points at which the segments intersect: A, B, and C.
These little bars look like line segments, which is why they appear over the names of the segments. When you refer to the LENGTHS of line segments, you don’t use the bars: AB, BC, and AC.
Note: Problems 1.1–1.3 refer to the diagram illustrated in Problem 1.1, triangle ABC.
1.2 List three different names for the largest angle of the triangle.
The largest angle of the triangle appears at the bottom of the diagram and has vertex B. One valid name of the angle is simply B; angles may be named using their vertices as long as the angle you are describing is clear. For example, if multiple angles share the same vertex, then simply identifying the vertex is not enough information.
In these cases, you name an angle using three points in a specific order: the first point lies on one side of the angle, the second point is the vertex of the angle, and the third point lies on the other side of the angle. Therefore, ABC and CBA are also valid names for the largest angle of this triangle.
To draw angle ABC, draw a straight line connecting A to B, and then draw a straight line from B to C. The vertex has to be the middle letter in the name of the angle.
Note: Problems 1.1–1.3 refer to the diagram illustrated in Problem 1.1, triangle ABC.
1.3 Are any of the angles in this triangle in standard position? Why or why not?
An angle in standard position satisfies the following conditions:
- One side of the angle overlaps the positive x-axis on the coordinate plane.
- The vertex of the angle overlaps the origin of the coordinate plane, the point at which the horizontal and vertical axes intersect.
Therefore, angles in standard position must be, by definition, drawn on the coordinate plane. Because this triangle is not plotted on a coordinate plane, none of its angles can be in standard position.
The diagram below represents one solution to this problem, though there are infinitely many correct answers. However, all answers must conform to two requirements. As Problem 1.3 explains, an angle in standard position has one side that lies along the positive x-axis. In other words, it overlaps the right half of the horizontal axis, like side 
in the diagram below. Note that the sides of angles in standard position are rays, which begin at a point (ray begins at point S), pass through a second specified point (in this case T), and continue in that direction.
The other characteristic of an angle in standard position is a vertex that lies on the origin of the coordinate plane, the point with coordinates (0,0) at which the x- and y-axes intersect. Note that point S, the vertex of angle RST, lies on the origin.
Because the two conditions (regarding one side of the angle and its vertex) are met, you conclude that angle RST is in standard position.
1.5 Is angle XYZ, illustrated below, in standard position? Why or why not?
Angle XYZ meets one requirement of an angle in standard position, because side 
lies along the positive x-axis. However, the second condition is not met; the vertex Y does not lie on the origin of the coordinate plane. Therefore, angle XYZ is not in standard position.
If you were to slide the angle to the left, keeping side on the positive x-axis, so that point Y overlapped the origin, the result would be angle XYZ in the diagram below, which is in standard position. Any angle may be placed in standard position if it is rotated and/or shifted properly.
Or you could just draw it in standard position to start with and save yourself the trouble.
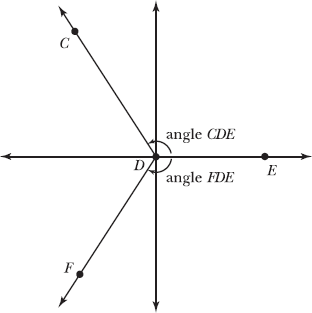
Note: Problems 1.6–1.8 refer to angle CDE in the diagram below. Note that angle CDE is in standard position.
1.6 Identify the initial and terminal sides of angle CDE.
The initial and terminal sides of an angle are, respectively, the sides at which the angles begin (initiate) and end (terminate). All angles in standard position share the same initial side, which lies along the positive x-axis. Therefore, the initial side of angle CDE is 
. The remaining side of the angle is the terminal side: 
.
Make sure to name the sides of the angle correctly. Unlike line segments, whose endpoints may be reversed when identifying a segment, the first point in a ray must be the vertex of the angle, which lies on the origin when an angle is in standard position. Notice that D (the vertex of angle CDE) appears first in both of the rays named above.
Note: Problems 1.6–1.8 refer to the diagram in Problem 1.6, which illustrates angle CDE in standard position.
1.7 Identify two angles in the coordinate plane that share the initial and terminal sides identified in Problem 1.6.
According to Problem 1.6, the initial side of the angle is and the terminal side is . Imagine that the angle is formed by a single ray, anchored at the origin, that begins along the positive x-axis and then rotates until it reaches its terminal position. Because you may rotate clockwise or counterclockwise from the initial side, you produce one of the two angles illustrated below.
Rotating counterclockwise produces a smaller angle (represented by the arrowed arc in the left portion of the diagram above) than rotating clockwise. Both of these angles share the same name: CDE. Furthermore, both of the angles share the same terminal side, so they are described as “coterminal.”
In trig, only the terminal side matters—not how you got to that terminal side. Both of the angles in this problem will have the same trigonometric values (which you’ll learn about in Chapters 2 and 3), even though they’re not the same size.
Note: Problems 1.6–1.8 refer to the diagram in Problem 1.6, which illustrates angle CDE in standard position.
1.8 Draw an angle in standard position whose measure is the opposite of angle CDE.
One of the fundamental assumptions of Euclidean geometry is that all angles have a positive angle measurement. However, angles assigned to the coordinate plane and placed in standard position allow you to measure in a more precise manner. In Problem 1.7, you identify two different angles with the same initial and terminal sides; the only difference between the two angles is the direction you travel, either clockwise or counterclockwise.
If you travel in a counterclockwise direction from the initial side of an angle to its terminal side, the angle formed has a positive measurement. Alternately, if you travel in a clockwise direction, the angle has a negative measurement. Assume, for the moment, that angle CDE is formed by traveling counterclockwise, beginning at the positive x-axis, rotating through the first quadrant, and coming to rest in the second quadrant.
The x- and y-axes divide the plane into four sections called quadrants, which are numbered like this:
To draw an angle in standard position that has a measure opposite of angle CDE, you simply rotate in the opposite direction. In the figure below, angle FDE is in standard position, so its initial side is the positive x-axis. The angle is formed by rotating clockwise through the fourth quadrant and coming to rest in the third quadrant at its terminal side, 
. This angle has the same measure as angle CDE, but it is negative rather than positive. Therefore, the angles have opposite measures.
