Common Angles on the Unit Circle
And their cosine/sine values
3.31 Expand the drawing you created in Problem 3.23 to include the following elements:
I. A unit circle passing through all four quadrants of the coordinate plane
II. The terminal sides of ![]() , π,
, π, ![]() , and 2π in standard position
, and 2π in standard position
II. The coordinates of the points at which the angles intersect the unit circle
Although a unit circle is simply a circle with a radius of 1, the term “unit circle” often refers to the drawing described in this problem. This diagram, duplicated in Appendix B for reference, lists the most commonly used angles in trigonometry, as well as their cosine and sine values.
Most teachers expect you to memorize this unit circle, including all of the angles and their coordinates.
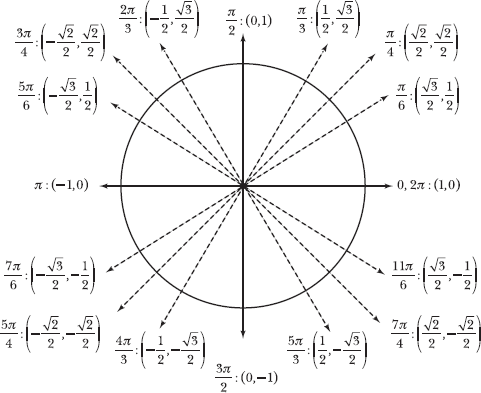
Problem 3.23 generates a single quadrant of the unit circle, but a clear pattern exists for the points in the other three quadrants. Though the signs of the coordinates change, the coordinates themselves remain constant:
- Angles with a denominator of 3 are paired with the point

- Angles with a denominator of 4 are paired with the point

- Angles with a denominator of 6 are paired with the point
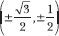
- Angles with a denominator of 1 or 2 have x- and y-coordinates of 0 or ±1
To help you generate the angles in the unit circle, consider the following observations:
- Angles in the first quadrant have a numerator of 1
- The numerators in the second quadrant are exactly one less than the denominators
- The numerators in the third quadrant are exactly one more than the denominators
- The numerators in the fourth quadrant are exactly one less than twice the denominators
It is very important that you can reproduce the entire unit circle from memory and recall coordinates given an angle (or vice versa). Most instructors expect you to identify the cosine and sine values of these angles without the use of a calculator.
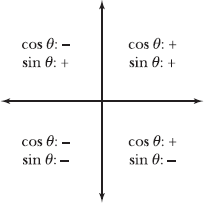
3.32 The diagram below indicates that both cosine and sine are positive for angles whose terminal sides lie in the first quadrant. Determine whether cosine and sine are positive or negative in the remaining three quadrants to complete the diagram, and justify your answer.

Recall that the cosine and sine of an angle on the unit circle are, respectively, the x- and y-coordinates of the corresponding points. Therefore, cosine is positive whenever a point is right of the origin, in quadrants I and IV. Cosine is negative in quadrants II and III.
Sine is positive whenever a point is above the origin, in quadrants I and II; sine is negative in quadrants III and IV.
3.33 Identify the signs of the tangent function in each of the four quadrants of the coordinate plane. Justify your answer.
Tangent is equal to the quotient of sine and cosine. To determine the sign of tangent in each quadrant, divide the sign of the sine function by the sign of the cosine function in that quadrant. For example, in quadrant I, both the sine and cosine are positive, and a positive number divided by a positive number is equal to a positive number.
![]()
Follow the same procedure for the remaining three quadrants.

Tangent is positive whenever cosine and sine have matching signs. In other words, when they are both positive (quadrant I) or both negative (quadrant III).
Note: Problems 3.34–3.35 explain how to identify trigonometric values based on the unit circle diagram you generated in Problem 3.31.
3.34 Assuming θ = ![]() is an angle in standard position, in what quadrant does its terminal side lie?
is an angle in standard position, in what quadrant does its terminal side lie?
To identify the quadrant in which an angle’s terminal side lies, note that each quadrant of the coordinate plane represents 90° or π/2 radians. Given an angle measured in radians, examine the number multiplied by π:
- If 0 < θ < 0.5, the terminal side lies in the first quadrant
- If 0.5 < θ < 1, the terminal side lies in the second quadrant
- If 1 < θ < 1.5, the terminal side lies in the third quadrant
- If 1.5 < θ < 2, the terminal side lies in the fourth quadrant
The number multiplied by π is 7/6 = ![]() which belongs to the interval 1 < θ < 1.5. Therefore, π = 7π/6 lies in the third quadrant.
which belongs to the interval 1 < θ < 1.5. Therefore, π = 7π/6 lies in the third quadrant.
Note: Problems 3.34–3.35 explain how to identify trigonometric values based on the unit circle diagram you generated in Problem 3.31.
3.35 Calculate ![]() .
.
According to Problem 3.31, angles of the unit circle with a denominator of 6 are associated with the coordinate ![]() . Problem 3.34 explains that the terminal side of θ = 7π/6 lies in the third quadrant, in which the x- and y-coordinates of points are both negative. Recall that the cosine of an angle is the x-coordinate of the associated point.
. Problem 3.34 explains that the terminal side of θ = 7π/6 lies in the third quadrant, in which the x- and y-coordinates of points are both negative. Recall that the cosine of an angle is the x-coordinate of the associated point.
If you memorize the unit circle, you don’t need to go through all of this logic to answer the question—you just write ![]() . This explanation is just meant to step you through the thought process that happens behind the scenes.
. This explanation is just meant to step you through the thought process that happens behind the scenes.
![]()
Note: Problems 3.36–3.37 explain how to identify trigonometric values based on the unit circle diagram you generated in Problem 3.31.
3.36 Assuming ![]() is an angle in standard position, in what quadrant does its terminal side lie?
is an angle in standard position, in what quadrant does its terminal side lie?
As Problem 3.34 explains, you can use the number multiplied by π in a radian angle measurement to identify the quadrant in which the terminal side lies: 3/2 = 1.5. Notice that this angle does not lie within the bounds of the third quadrant (1 and 1.5), nor does it lie within the bounds of the fourth quadrant (1.5 and 2). Instead, it is the boundary of the third and fourth quadrants, the negative y-axis. Angles like θ = 3π/2, whose terminal sides lie on the x- or y-axes, are called “quadrantals.”
Note: Problems 3.36–3.37 explain how to identify trigonometric values based on the unit circle diagram you generated in Problem 3.31.
3.37 Calculate ![]() .
.
As the diagram in Problem 3.31 illustrates, the angle θ = 3π/2 in standard position intersects the unit circle at point (0,–1). The y-coordinate of this point represents the sine value of θ.
![]()
The angle θ = 3π/4 intersects the unit circle at point ![]() . The y-coordinate of this point represents the sine value of the angle.
. The y-coordinate of this point represents the sine value of the angle.
![]()
Don’t keep looking back at the unit circle you made in Problem 3.31. At this point, you need to have those angles, their cosines, and their sines memorized.
Note that the sines of angles terminating in the second quadrant, like the y-coordinates of points in the second quadrant, are positive.
3.39 Calculate ![]() without the use of a trigonometric table or a graphing calculator.
without the use of a trigonometric table or a graphing calculator.
The terminal side of angle θ = 2π/3 intersects the unit circle at point ![]() ; the cosine of θ is the x-coordinate of this point.
; the cosine of θ is the x-coordinate of this point.
![]()
3.40 Calculate ![]() without the use of a trigonometric table or a graphing calculator.
without the use of a trigonometric table or a graphing calculator.
The terminal side of angle θ = 11π/6 intersects the unit circle at point ![]() ; the cosine of θ is the x-coordinate of this point.
; the cosine of θ is the x-coordinate of this point.
![]()
Ensure that you are reporting the correct signs in your final answer. Because θ = 11π/6 lies in the fourth quadrant, its cosine is positive and its sine is negative.
3.41 Calculate ![]() without the use of a trigonometric table or a graphing calculator.
without the use of a trigonometric table or a graphing calculator.
The terminal side of angle θ = 4π/3 intersects the unit circle at point ![]() in the third quadrant. Therefore, sin
in the third quadrant. Therefore, sin ![]()
Recall that the cosine of an angle is equal to the quotient of its cosine and sine values.
See the margin note next to Problem 2.28.
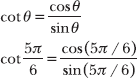
The terminal side of π = 5π/6 intersects the unit circle in the second quadrant at point ![]() . The x-coordinate of the point represents its cosine value, and the y-coordinate represents its sine value.
. The x-coordinate of the point represents its cosine value, and the y-coordinate represents its sine value.
![]()
Multiply the numerator and denominator by 2 to reduce the complex fraction.

3.43 Calculate csc π without the use of a trigonometric table or a graphing calculator.
The cosecant function is defined as the reciprocal of the sine function.
![]()
The terminal side of θ = π, which lies along the negative x-axis, intersects the unit circle at point (–1,0). Therefore, sin π = 0. Substitute this value into the equation above.
![]()
Division by zero is an undefined operation. Therefore, you conclude that csc π is undefined.
No cosecant value exists for π or any multiple of π. You’ll see this more clearly when you graph cosecant at the end of Chapter 6—there are big linear asymptotes where the graph doesn’t exist.
Note that the “0” in this problem represents the angle measurement 0 radians, which describes an angle whose initial and terminal sides overlap on the positive x-axis. The tangent function is equal to the quotient of the sine and cosine functions.
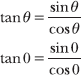
The terminal side of angle θ = 0 lies along the positive x-axis and intersects the unit circle at point (1,0). Therefore, sin θ = 0 and cos θ = 1.

The tangent of an angle measuring 0 radians is equal to 0.
3.45 Calculate sin–1 1 without the use of a trigonometric table or a graphing calculator.
Inverse trigonometric functions provide a trigonometric value and ask you to identify the angle associated with that value. For example, sin–1 1 asks this question: “What angle θ has a sine value of 1?” Recall that the sine of an angle is equal to its y-coordinate on the unit circle.
Consider the diagram you created in Problem 3.31; only one point on that diagram has a y-coordinate of +1, the point that corresponds with central angle θ = π/2. Therefore, sin–1 1 = π/2.
