Secant
U-shaped pieces that shoot off of the cosine graph
Note: Problems 6.11–6.13 explore the graph of f(θ) = sec θ.
6.11 Draw the graph of y = cos θ as a dotted curve on the coordinate plane and use the graph to determine the domain and period of f(θ) = sec θ.
Notice that sec θ = 1/cos θ and tan θ = (sin θ)/(cos θ) have the same denominator, cos θ. They also have the same domain, because they are both undefined only when cos θ = 0. Problem 6.2 states that the domain of tan θ is all real numbers such that θ ≠ kπ/2, where k is an odd number; that is also the domain of f(θ) = sec θ.
If cos θ = 0 then ![]() , but you aren’t allowed to divide by 0.
, but you aren’t allowed to divide by 0.

The function values of f(θ) = sec θ are equal to the reciprocals of the corresponding values of cos θ, so they repeat when the values of cos θ repeat. Because y = cos θ has period 2π, you conclude that f(θ) = sec θ also has period 2π.
In other words, if f(x) is the reciprocal of periodic function g(x), then f(x) and g(x) have the same period.
Note: Problems 6.11–6.13 explore the graph of f(θ) = sec θ.
6.12 Demonstrate how the graph of f(θ) = sec θ can be generated from the graph you created in Problem 6.11.
Recall that sec θ and cos θ are reciprocal functions. Therefore, the larger one function is, the smaller the other is. For example, according to the unit circle, cos π/3 = 1/2. The corresponding value of secant is larger: ![]() Given an even smaller cosine value, the secant grows even larger: if cos θ = 1/100, then
Given an even smaller cosine value, the secant grows even larger: if cos θ = 1/100, then ![]() .
.
Graphically speaking, as the graph of cos θ gets closer to the x-axis, the graph of sec θ increases or decreases without bound. As illustrated in the following graph, f(θ) = sec θ has the same vertical asymptotes as the graph of y = tan θ; both are undefined at θ = kπ/2, where k is an odd number. As the graph of f(θ) = sec θ approaches the vertical asymptotes at those values, the function values are very large positive or negative numbers, like the graph of tan θ.
If cosine is tiny and positive, secant is a huge positive number; if cosine is tiny and negative, then secant is a huge negative number.

Notice that the graphs of cos θ and sec θ share point (0, 1). According to the unit circle, cos 0 = 1, and the reciprocal of 1 is 1. Similarly, the graphs share point (π, –1) because cos π = sec π = –1.
Note: Problems 6.11–6.13 explore the graph of f(θ) = sec θ.
6.13 Use the graph you generated in Problem 6.12 to identify the range of f(θ).
Horizontal lines drawn on the coordinate plane intersect the graph of f(θ) at height f(θ) = 1 and above, as well as height f(θ) = –1 and below. However, the graph does not exist between heights of –1 and 1. Therefore, the range of f(θ) is all real numbers excluding any value y such that –1 < y < 1. In interval notation, the range of f(θ) is ![]() .
.
Begin with the graph of y = sec θ and apply two transformations. Multiplying a function by –1 reflects it across the x-axis, and subtracting 1 from it moves the graph down 1 unit.
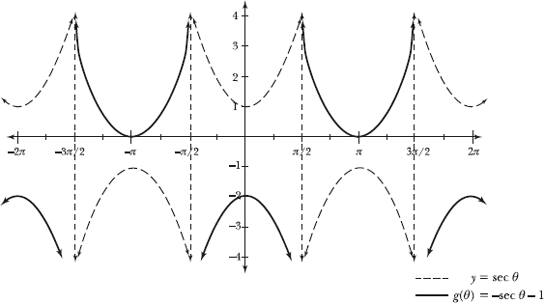
6.15 Graph h(θ) = sec (3θ).
Consider one period of the untransformed secant graph, beginning at θ = 0 and ending at θ = 2π. The graph of h(θ) will contain three full periods of this shape in the same horizontal interval, as illustrated below.

