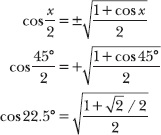Win half an argument by being radical
8.22 Generate the cosine half-angle formula based on its power-reducing formula.
Substitute θ = x/2 into the cosine power-reducing formula, and solve the equation for cos (x/2).
Look at Problem 8.17 to review the power-reducing formulas.
Note that the half-angle formula contains a “±” symbol, because the formula, itself, is not sufficient to determine the sign of cos (x/2). Instead, you must use additional information given by the problem, such as the quadrant in which the angle lies.
8.23 Substitute θ = 
into the power-reducing formula for sin2 θ to generate the half-angle formula for sine.
Apply the technique demonstrated in Problem 8.22.
8.24 Apply a half-angle formula to calculate the exact value of cos 22.5° without using a calculator or trigonometric table.
Although you have not memorized the value of cos 22.5°, you have memorized the trigonometric values for twice that angle: 2(22.5°) = 45°. To calculate cos 22.5°, substitute 45° into the half-angle formula presented in Problem 8.22. Note that an angle in standard position that measures 22.5° terminates in the first quadrant, so cos 22.5 > 0.
Sine and cosine are both positive in the first quadrant.
Express the complex fraction as a sum of two fractions with a denominator of 2. Note that 
.
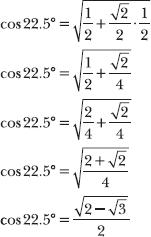
8.25 Apply a half-angle formula to calculate the exact value of sin 
without using a calculator or trigonometric table.
Apply the method demonstrated in Problem 8.24, substituting 11π/6 into the half-angle formula for sine, because 11π/12 is half of 11π/6. Note that the angle 11π/12 lies in the second quadrant because 
. (According to the technique described in Problem 3.34, the angle lies in the second quadrant because 
.) Recall that sine values are positive for angles in the second quadrant, so you should replace the “±” sign in the half-angle formula with a “+” sign.
.This expression resembles the cosine half-angle formula 
, if θ = 12x.
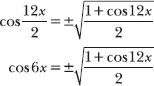
Therefore, you can conclude that 
is equal to ± cos 6x. Note, however, that the radical expression given in the problem is positive, so cos 6x must be positive as well. Surround cos 6x with absolute value signs to ensure that its value is greater than zero.
8.27 Simplify the expression using a half-angle formula: 
.
This radical expression resembles the sine half-angle formula 
, if θ = 5x.
The problem states that the radical expression is negative. To ensure that the equivalent expression sin (5x/2) is also negative, surround it with absolute value bars and then take its opposite.
The absolute value bars work just like they did in Problem 8.26. Then, you multiply that absolute value expression (which HAS to be positive) by –1, so the product HAS to be negative.
The solution 
is also correct.