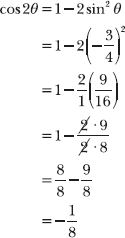Ditch the 2s in sin 2x and cos 2y
8.1 Express sin 2x as a product of single-angle trigonometric functions.
The expression sin 2x is described as a “double angle,” because the argument of the expression is 2x rather than simply x. The identity below allows you to rewrite the double-angle expression sin 2x as the product of two single-angle expressions.
sin 2x = 2 sin x cos x
8.2 Verify your answer to Problem 8.1 by applying the sum formula for sine.
Apply the sum formula for sine to expand sin 2x. Note that sin 2x = sin (x + x).
This formula comes from Problem 7.34.

8.3 Simplify the expression: ![]() .
.
Apply the double-angle identity sin 2x = 2 sin x cos x to expand the numerator, and then simplify the fraction.

8.4 Calculate sin 2θ, given cosθ ![]() .
.
This problem provides the cosine of θ and indicates that θ terminates in the second quadrant. Apply the technique modeled in Problems 4.30–4.45 (and again in Problem 7.45) to calculate sin θ. Note that sin θ = +5/13. Substitute the known values of cos θ and sin θ to calculate sin 2θ.
Draw a right triangle in the second quadrant with an adjacent side with signed length –12 and a hypotenuse with length 13. Then use the Pythagorean theorem to calculate the signed length of the opposite side: +5.

Apply the technique described in Problem 8.4 to calculate the value of cos α, knowing α terminates in the fourth quadrant and sin α = –1/4. According to the Pythagorean theorem, cosα![]() . Note that cos α > 0 because angles in the fourth quadrant have positive cosine values and negative sine values. Substitute cos α and sin α into the sine double-angle formula to calculate sin 2α.
. Note that cos α > 0 because angles in the fourth quadrant have positive cosine values and negative sine values. Substitute cos α and sin α into the sine double-angle formula to calculate sin 2α.
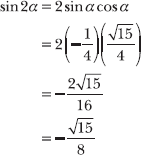
8.6 Verify the statement: (1 – cos 2x)(1 + cos 2x) = 4 sin2 x cos2 x.
Multiply the terms left of the equal sign.
![]()
According to a Pythagorean identity, cos2 x + sin2 x = 1. This identity is true for any value of x. For example, if you replace x with 2x, the identity remains valid: cos2 2x + sin2 2x = 1. If you subtract cos2 2x from both sides of the new identity, the result is sin2 2x = 1 – cos2 2x. Use this equality statement to rewrite the left side of the equation above.
sin2 2x = 4 sin2 x cos2 x
Note that sin2 2x = (sin 2x)(sin 2x).

8.7 Verify the statement: ![]() .
.
Recall that csc x and sin x are reciprocal functions. Therefore, ![]() . Use this equality statement to rewrite the left side of the statement. Express the right side of the statement in terms of sine and cosine.
. Use this equality statement to rewrite the left side of the statement. Express the right side of the statement in terms of sine and cosine.

Combine the fractions on the right side of the equation using least common denominator 2 sin x cos x.

According to a Pythagorean identity from Problem 7.23, cos2x + sin2x = 1.
8.8 Rewrite the double-angle expression cos 2x as a difference of single-angle cosine and sine expressions.
There are three different ways to convert the double-angle expression cos 2x into a single-angle expression, but only one way that contains both sine and cosine: cos 2x = cos2 x – sin2 x.
Be careful with the sign:
cos2 x + sin2 x = 1
cos2 x – sin2 x = cos 2x
8.9 Verify your answer to Problem 8.8 using the sum formula for cosine.
Notice that 2x = x + x. Apply the sum formula for cosine (originally stated in Problem 7.37) to expand cos (x + x).

8.10 Apply a Pythagorean identity to rewrite your solution to Problem 8.8 in two different ways: (A) in terms of cosine only, and (B) in terms of sine only.
If you subtract cos2 x from both sides of the Pythagorean identity cos2 x + sin2 x = 1, the result is sin2 x = 1 – cos2 x. Use this equality statement to rewrite the cosine double-angle formula in terms of cosine.

Similarly, you can manipulate the Pythagorean identity cos2 x + sin2 x = 1 to assert that cos2 x = 1 – sin2 x. Use this equality statement to rewrite the cosine double-angle formula in terms of sine.
Thus, there are three equivalent ways to rewrite cos 2x using single-angle trigonometric expressions.
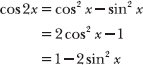
8.11 Verify the statement: sin 4x = 4 cos3 x sin x – 4 cos x sin3 x.
Note that 4x = 2x + 2x and apply the sum formula for sine to expand sin 4x.

Thus, sin 4x is equal to 4 cos3 x sin x – 4 cos x sin3 x, as proposed in the original problem, and the statement is verified.
8.12 Express cos 3x in terms of single-angle cosine functions.
Note that 3x = x + 2x, and apply the sum formula for cosine.
![]()
Apply the double-angle formula cos 2x = 2 cos2 x – 1, because the problem directs you to write the expression in terms of cosine.
Instead of cos2 x – sin2 x and 1 – 2 sin2 x, because each of those contains sine.
![]()
According to a Pythagorean identity, sin2 x = 1 – cos2 x.
You get this by subtracting cos2 x from both sides of the identity cos2 x + sin2 x = 1.

Factor the difference of perfect squares in the numerator. Notice that rewriting the denominator as 5 (2 sin θ cos θ) allows you to apply the sine double-angle formula.

8.14 Use a double-angle formula to verify that cos![]()
To use the double-angle formula, you need to find an angle you can double to get π/3:![]()
Multiplying π/6 by 2 produces the angle π/3. Therefore, you can substitute π/6 into the cosine double-angle formula to verify that cos (π/3) = 1/2, as dictated by the unit circle. The following solution applies the double-angle formula cos 2x = cos2 x – sin2 x, but all three of the cosine double-angle formulas produce the same result.
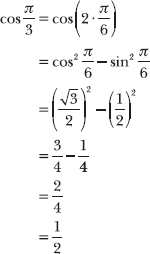
8.15 Calculate cos 2θ, given sin ![]() and
and ![]() .
.
Unlike Problems 8.4–8.5, in which you needed to construct a right triangle to calculate missing trigonometric values, knowing that sin θ = –3/4 is sufficient to complete this problem—as long as you select the correct cosine double-angle formula.
8.16 Simplify the expression: ![]() .
.
Apply a cofunction identity and a reciprocal identity to rewrite the bracketed expression and then distribute –2 sin x to each term.

Apply two double-angle formulas to simplify the expression: sin 2x = 2 sin x cos x and cos 2x = 1 – 2 sin2 x.