![]()
Note: Problems 3.1–3.3 refer to the diagram below, featuring right triangle XYZ, in which XY = YZ.
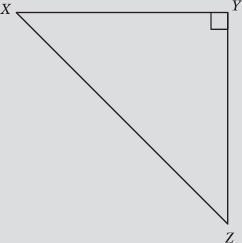
3.1 Given ![]() in the triangle, explain why both acute angles measure 45°.
in the triangle, explain why both acute angles measure 45°.
All triangles contain three angles whose measures have a sum of 180° = π radians. Apply this geometric theorem to the given triangle by adding the measures of angles X, Y, and Z, and setting the sum equal to 180°.
![]()
In this diagram, angle Y is a right angle, so ![]() . Furthermore, you are given
. Furthermore, you are given ![]() . Therefore, you can substitute 90° for
. Therefore, you can substitute 90° for ![]() and
and ![]() for
for ![]() in the angle sum equation above.
in the angle sum equation above.
![]()
Note that ![]() .
.
![]()
Solve the equation for ![]() .
.

So once you subtract the right angle from 180°, you are left with 90°. Because the two remaining angles have the same measure, you have to divide the leftover 90° by 2. That gives you two angles that each measure 45°.
You conclude that ![]() . Therefore, triangle XYZ is a 45°–45°–90° triangle, a geometric classification based upon the measures of its angles.
. Therefore, triangle XYZ is a 45°–45°–90° triangle, a geometric classification based upon the measures of its angles.
Note: Problems 3.1–3.3 refer to the diagram in Problem 3.1, in which XY = YZ.
3.2 Let l represent the length of a leg of triangle XYZ. Apply the Pythagorean theorem to calculate XZ in terms of l.
According to the Pythagorean theorem, given a right triangle with legs of length a and b and a hypotenuse of length c, you can conclude that a2 + b2 = c2. In this problem, the legs of the triangle are ![]() and
and ![]() the hypotenuse is
the hypotenuse is ![]() .
.
![]()
This problem states that each leg has length l. Thus, l = XY = YZ.
To calculate the length of XZ in terms of l, solve the equation for XZ.

This may feel familiar. It’s a geometry theorem that is often written ![]() · L, where H is the hypotenuse length and L is the leg length.
· L, where H is the hypotenuse length and L is the leg length.
Therefore, the length of the hypotenuse is ![]() times the length of the leg, l.
times the length of the leg, l.
Note: Problems 3.1–3.3 refer to the diagram in Problem 3.1, in which XY = YZ.
3.3 Given XZ = 7, calculate the lengths of the legs.
According to Problem 3.2, the hypotenuse of a 45°–45°–90° triangle is equal to ![]() times the length of a leg.
times the length of a leg.
(length of the hypotenuse)= ![]() (length of a leg)
(length of a leg)
Let l represent the length of a leg of triangle XYZ; note that XZ = 7 is the length of the hypotenuse.

The length of the leg, l, is a fraction with an irrational denominator. Traditionally, radicals within a denominator are eliminated in a process called “rationalizing the denominator.”
![]()
Multiply the numerator and denominator by the offending square root: ![]() .
.
You conclude that the lengths of the legs are ![]() .
.
3.4 Calculate the length of the legs of an isosceles right triangle if its hypotenuse has length ![]() .
.
Recall that the hypotenuse of an isosceles right triangle is ![]() times the length of a leg. Let l represent the length of the leg and
times the length of a leg. Let l represent the length of the leg and ![]() represent the length of the hypotenuse in the following equation.
represent the length of the hypotenuse in the following equation.
In other words, a 45°–45°–90° triangle
![]()
Solve for l.

Both legs of the isosceles right triangle have length ![]() .
.
Note: Problems 3.5–3.8 apply the properties of 45°–45°–90° triangles to the coordinate plane in order to generate coordinates on a unit circle.
3.5 Draw a unit circle on the coordinate plane with central angle θ in standard position, given ![]() .
.
A unit circle has radius 1 and is centered at the origin of the coordinate plane. Recall that an angle in standard position has an initial side on the positive x-axis and a vertex that lies on the origin, as explained in Problems 1.3–1.5. You wish to convert the radian angle measure π/4 into degrees to help visualize where its terminal side lies in the coordinate plane.
![]()
See Problem 1.27 if you can’t remember how to convert from radians to degrees. Also, check out Problem 1.17, which helps you visualize common angles in radians.
Draw the unit circle and θ on the same coordinate plane, as illustrated in the following diagram. Notice that the terminal side of angle θ is also a radius of the circle, and recall that a unit circle has radius r = 1.

Because you are constructing a 45° angle in the coordinate plane, you can apply the properties of 45°–45°–90° triangles (specifically that the hypotenuse of such a triangle is ![]() times the length of a leg) in Problems 3.6–3.8.
times the length of a leg) in Problems 3.6–3.8.
Note: Problems 3.5–3.8 apply the properties of 45°–45°–90° triangles to the coordinate plane in order to generate coordinates on a unit circle.
3.6 Consider the diagram you created in Problem 3.5, a unit circle with central angle θ that measures ![]() radians. Draw a right triangle in the coordinate plane whose legs represent the horizontal and vertical distances between the origin and the point at which the terminal side of θ intersects the unit circle.
radians. Draw a right triangle in the coordinate plane whose legs represent the horizontal and vertical distances between the origin and the point at which the terminal side of θ intersects the unit circle.
The following diagram specifically examines the first quadrant of the drawing generated in Problem 3.5; the origin is labeled point A. Notice that C is the point at which the terminal side of θ intersects the unit circle. A vertical segment extends from C to the x-axis, intersecting it at point B.
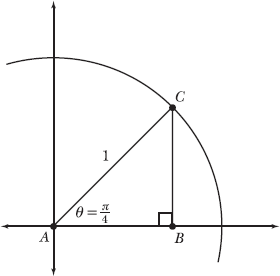
Because the x-axis is horizontal and ![]() is vertical, they form right angle ABC. Therefore, triangle ABC is a right triangle, with a right angle measuring π/2 and two acute angles, each measuring π/4.
is vertical, they form right angle ABC. Therefore, triangle ABC is a right triangle, with a right angle measuring π/2 and two acute angles, each measuring π/4.
![]() triangle is the same thing as a 45°–45°–90° triangle, but it’s written in radians instead of degrees.
triangle is the same thing as a 45°–45°–90° triangle, but it’s written in radians instead of degrees.
Note that AB represents the horizontal distance between the origin and point C; similarly, BC represents the vertical distance between the origin and point C.
Note: Problems 3.5–3.8 apply the properties of 45°–45°–90° triangles to the coordinate plane in order to generate coordinates on a unit circle.
3.7 Calculate the lengths of the sides of the right triangle you identified in Problem 3.6.
The hypotenuse of right triangle ABC below is also the radius of the unit circle, so it has length AC = 1. Let l represent the length of the legs.
Remember, 45°–45°–90° triangles are automatically isosceles.

As Problems 3.2–3.3 explain, right triangles with acute angles measuring π/4 radians (or 45°) have hypotenuses that are ![]() times the lengths of their legs.
times the lengths of their legs.

Solve for l.

Rationalize the denominator by multiplying both the numerator and denominator by ![]() .
.

You conclude that AB = CB = ![]() .
.
Note: Problems 3.5–3.8 apply the properties of 45°–45°–90° triangles to the coordinate plane in order to generate coordinates on a unit circle.
3.8 Identify the coordinates of the point at which the terminal side of θ intersects the unit circle.
The diagram below summarizes the conclusions drawn in Problems 3.5–3.7. Of specific interest are the lengths calculated in Problem 3.7, which represent the horizontal and vertical distances between the origin and point C.

Because AB = ![]() , point C is
, point C is ![]() units right of the origin; therefore, the x-coordinate of point C is
units right of the origin; therefore, the x-coordinate of point C is ![]() . Similarly, the y-coordinate of point C is
. Similarly, the y-coordinate of point C is ![]() because BC =
because BC = ![]() .
.
![]()
Like triangle ABC in Problems 3.6–3.8, this right triangle has two acute angles that measure π/4 and a hypotenuse of length 1 (because it is a radius of the unit circle). Therefore, the legs of the right triangle have the same lengths as the legs in triangle ABC: ![]() .
.
Note that the x-coordinate of point P must be negative, because P is in the second quadrant; you must travel left from the origin to reach P. Hence, the coordinates of P are (–![]() ,
, ![]() ).
).
The signs of the coordinates tell you what direction to travel from the origin in order to reach the point:
+x coordinate: go right
–x coordinate: go left
+y coordinate: go up
–y coordinate:
go down.

