Trigonometric Tables

When “close enough” is good enough

Before scientific and graphing calculators were readily available to scientists, engineers, and mathematics students, other tools were necessary to calculate trigonometric values. Greek mathematicians constructed the first trigonometric tables, and they have been used for over two thousand years to assist in the approximation and estimation of trigonometric functions. Although you will use a calculator for the vast majority of this book, this section of problems demonstrates that you can still derive surprisingly accurate estimations using historical methods.

Here’s the real reason trig tables are included in the book: Because some teachers still teach them, even though technology gives you faster, more accurate answers.

In Appendix A, angles between 0° (0 radians) and 90° (π/2 radians) are listed in quarter degree increments. The first column represents an angle in degrees; the second column represents the angle in radians; and then the next six columns, in order, list the cosine, sine, tangent, secant, cosecant, and cotangent values of that angle. Locate the row of the table that begins with 88°.

According to this row of the table, sin 88° ≈ 0.99939. All values in the table are accurate to five decimal places.

In order to approximate the angle θ that has a tangent value of 0.68728, consult the tangent column in the table and look for the value 0.68728. Notice that the tangent values increase as the angle increases, so the larger the angle, the larger the tangent value.

The row corresponding to 34.50° (0.60214 radians) contains the precise tangent value for which you are searching: 0.68728.

Therefore, you conclude that θ ≈ 0.60214 radians if tan θ = 0.68728. Remember that this trigonometric table is accurate to five decimal places, but nearly all of the values in the table are rounded. Thus, you cannot conclude that θ is exactly equal to 0.60214 radians.

Different trigonometric functions exhibit different behavior on different intervals, so this problem specifically identifies the interval described in Appendix A, 0° to 90°. In Problems 2.32–2.36, you use the table in Appendix A to approximate unlisted trigonometric values; when you do, it is important to know whether successive rows in the table increase or decrease for the specific trigonometric function you are investigating.

Three of the trigonometric functions increase between 0° and 90°: sine, tangent, and secant. The remaining three functions, termed the “cofunctions” because their names are derived by adding the prefix “co-” to the three functions already listed, decrease: cosine, cotangent, and cosecant.

Here’s one way to remember which functions decrease: “If it’s a CO-, down it goes!”

You are given an angle measured in degrees, and each row of the table represents a degree measurement exactly 0.25° larger than the preceding row. Therefore, the rows that bound 45.11° are 45.00° and 45.25°; they are duplicated below.

As Problem 2.31 explains, the tangent function increases as the angles increase between 0° and 90°. According to the shaded values in the previous table, tan 45° = 1 and tan 45.25° ≈ 1.00876. Thus, 1 < tan 45.11° < 1.00876.

In other words, because 45.11 is between 45 and 45.25, its tangent value is between the tangent values of 45 and 45.25.

According to Problem 2.32, 45.11° falls between the 45.00° and 45.25° rows in the trigonometric table, so its value, x = tan 45.11°, falls between 1 and 1.00876. It may be helpful to imagine a new row of the table that represents 45.11°, as illustrated by the shaded row in the table below.

Estimating trigonometric values based upon values that bound them is called “interpolating.” You assume, for the sake of approximation, that the angles and their corresponding trigonometric values have a linear relationship on very small intervals. While this is not true, it does provide a reasonably rough estimate.

Trig graphs are not straight lines, but any graph sort of looks like a straight line if you look at a very tiny piece of it. This is a concept called “local linearity.”

Consider the three equations below, which summarize the important information from the trigonometric table. The left sides of the equations contain the three angles in the problem (45°, 45.11°, and 45.25°), and the right sides contain the corresponding tangent values for those angles (1, the unknown value x, and 1.00876).

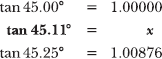
In the proportion, you will compare differences: How different are two angles when compared to their tangent values? Begin by comparing the values given in the trig table. When an angle increases from 45.00° to 45.25° (for a total increase of 45.25° – 45.00° = 0.25°), the tangent value increases from 1.0 to 1.00876 (for a total increase of 1.00876 – 1 = 0.00876).

Now conduct the same comparison for the new angle, 45.11°, and the bounding angle below it, 45.00°. In other words, note that an angle increase of 45.11° – 45.00° = 0.11° corresponds to a tangent value increase of x – 1.

You are left with four different values, two that compare angle differences and two that compare tangent value differences. Substitute them into the following proportion:

Cross-multiply and solve for x.

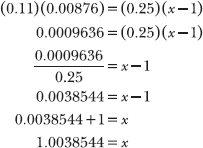
Multiply the top of the left fraction by the bottom of the right fraction and vice versa. Set those two products equal.

The problem instructs you to round this answer to the nearest hundred thousandth, so you should round to the fifth decimal place: x ≈ 1.00385. Therefore, tan 45.11° ≈ 1.00385.

The actual value of tan 45.11° is 1.0038471150116471310256758144812…, so the estimate is very accurate for the first four decimal places and less so after that.

Although the angles in the table are listed in increments of 0.25°, the radian equivalents of those angles are listed in the second column. Use a calculator to compute the decimal equivalent of the angle.

Now identify the two rows within the trigonometric table that bound 0.285599 radians. These rows are copied on the next page.

Note that the angle 0.285599 falls between the rows containing radian values of 0.28362 and 0.28798. Therefore, the cos 0.285599 will fall between 0.95882 and 0.96005.

According to Problem 2.34, cos π/11 lies somewhere within the interval bounded above by 0.96005 and below by 0.95882.

Apply the technique described in Problem 2.33, comparing angle differences to trigonometric value differences, as illustrated below.

Make sure to subtract in the same order each time. In the computations above, values from the upper rows are always subtracted from values in rows below them. This leads to the negative value –0.00123 among the results, because the larger the angle in the table, the smaller its cosine value.

Substitute the four differences into the interpolation proportion.

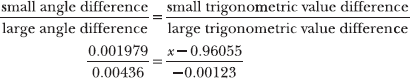
Remember, “co” functions decrease in the table, so the “large trigonometric value difference” in the proportion is negative.

Cross-multiply and solve for x.

You conclude that cos π/11 ≈ 0.960. The actual value is 0.9594929736, so the estimate is reasonably accurate.

In this problem, you are given a trigonometric value and are asked to identify the corresponding angle. Begin by identifying the two consecutive rows in the table with sine values that bound 0.89835 above and below.

Apply the procedure modeled in Problems 2.33 and 2.35, calculating the proportional differences between angles and their trigonometric values.

Construct a proportion that relates the differences calculated above.

Solve the proportion for θ.

You conclude that θ ≈ 63.943°.

The actual angle (accurate to seven decimal places) is 63.9420226°.