Polar Coordinates
Plot points using distances and angles
Note: In Problems 17.15–17.17, point A has polar coordinates (r,θ) = ![]()
17.15 Explain how to interpret the polar coordinate 3 of point A.
The first coordinate of a point in polar form is called the radial coordinate or radius, usually written r in the coordinate pair (r,θ). This value represents the distance between the point and a fixed location called the pole. The pole is typically defined as the origin of the coordinate system, so point A is a distance of 3 units from the origin. This is not sufficient information to plot point A, because there are infinitely many points on the plane that are r = 3 units away from the origin.
Note: In Problems 17.15–17.17, point A has polar coordinates (r,θ) = ![]()
17.16 Explain how to interpret the polar coordinate π/6 of point A.
The second coordinate of a point in polar form is called the angular coordinate or polar angle, θ in the coordinate pair (r,θ). This value identifies an angle in the coordinate plane, measured from a ray called the polar axis. Typically, the polar axis is the positive x-axis.
Recall that positive angles in the coordinate plane are measured in the counterclockwise direction and negative angles are measured in the clockwise direction. Thus, point A lies along the ray that forms a π/6 = 30° angle with the positive x-axis.
Note: In Problems 17.15–17.17, point A has polar coordinates (r,θ) = ![]()
17.17 Plot A in the coordinate plane.
Consider the following diagram. The point represents the pole, the ray represents the polar axis, and the concentric circles centered at the pole represent fixed distances from the pole. In other words, any point with a radial coordinate of 3 lies on the circle centered at the origin with radius 3—the darkened circle in the diagram.
Concentric circles have the same center, in this case the pole.
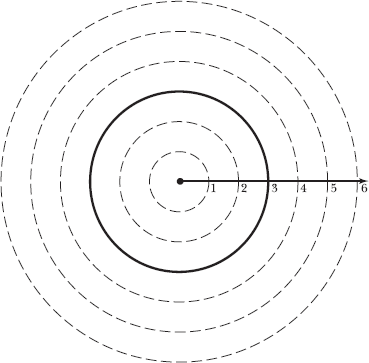
According to Problem 17.16, the angular coordinate identifies the ray upon which point A lies. The angular coordinate is θ = π/6, so point A lies at the intersection of the darkened circle with radius 3 and the ray that forms a π/6, or 30°, angle with the polar axis.

Note: In Problems 17.18–17.21, you plot four similar points to explore how negative signs affect polar coordinates.
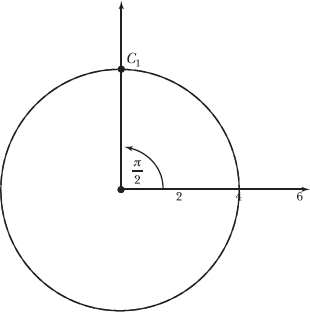
17.18 Plot the following point, expressed in polar coordinates: ![]()
The positive y-axis forms a π/2 (or 90°) angle with the polar axis, so C1 is located on that ray. Furthermore, C1 is located 4 units away from the pole, as illustrated below.
Note: In Problems 17.18–17.21, you plot four similar points to explore how negative signs affect polar coordinates.
17.19 Plot the following point, expressed in polar coordinates: C2 = ![]()
Negative angular coordinates are measured in the clockwise direction, so C2 lies on the ray directly below the pole, whereas point C1 in Problem 17.18 lies on the ray directly above the pole.
Note: In Problems 17.18–17.21, you plot four similar points to explore how negative signs affect polar coordinates.
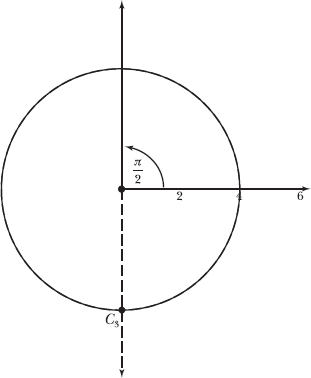
17.20 Plot the following point, expressed in polar coordinates: C3 = ![]()
When the radial coordinate of a point is negative, the point does not lie on the ray described by the angular coordinate. Instead, it lies on the opposite ray. In this problem, C3 does not lie along the ray measuring θ = π/2; it lies along the opposite ray, the dotted ray in the figure below.
The second coordinate identifies a specific ray. If the first coordinate is positive, then the point lies on that ray. If the first coordinate is negative, the point lies on the opposite ray.
Note: In Problems 17.18–17.21, you plot four similar points to explore how negative signs affect polar coordinates.
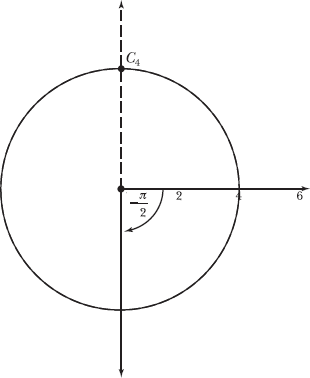
17.21 Plot the following point, expressed in polar coordinates: C4 = ![]()
Like Problem 17.19, this point has an angular coordinate of –π/2. However, the radial coordinate is also negative, so C4 lies on the opposite ray, the dotted ray in the diagram below.
17.22 Plot the following point, expressed in polar coordinates: p = ![]()
Plot the ray in the counterclockwise direction that forms a 3π/4 angle with the polar axis. Because the radial coordinate is positive, P is located 2 units away from the pole along that ray.

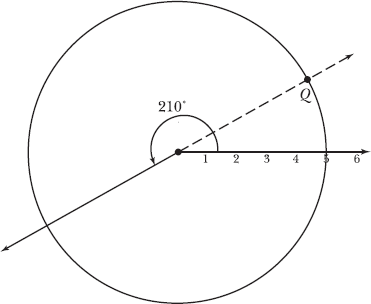
Note: In Problems 17.23–17.24, point Q has polar coordinates (–5,210°).
The angular coordinate could be measured in degrees or radians.
17.23 Plot point Q.
In the diagram below, the solid ray is 210° from the polar axis in the counterclockwise direction. Because the radial coordinate is negative, Q lies on the opposite ray, 5 units from the pole.
Note: In Problems 17.23–17.24, point Q has polar coordinates (–5,210°).
17.24 Construct polar coordinates (r,θ) for point Q such that the radial coordinate is positive and the angular coordinate is both positive and acute.
There is only one way to write a point using rectangular coordinates, but there are infinitely many ways to identify the same point using polar coordinates.
The reference angle for a 210° angle is a 30° angle, as illustrated below. Point Q lies 5 units away from the pole on the dotted ray in the diagram, which is 30° from the polar axis. Therefore, Q = (5,30°).

17.25 Given point P = (1,0) expressed in rectangular coordinates, identify two points in polar form that coincide with P.
Point P lies on the polar axis, exactly r = 1 unit away from the pole. The angular coordinates θ = 0 and θ = 2π (or θ = 0° and θ = 360°) both describe the polar axis, so the points (1,0) and (1,2π)—or (1,0°), and (1,360°)—both represent P in polar form. All of these points coincide; they describe the same point in the coordinate plane.
These are not the only solutions to this problem. If the radial coordinate is r = 1, any angle coterminal to 2π is also a valid angular coordinate, so (1,4π), (1,6π), and (1,–2π) are also polar representations of P.
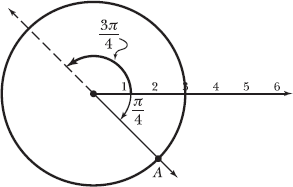
Note: In Problems 17.26–17.29, you identify four different points in polar form that coincide with point A, illustrated below.

17.26 Identify coordinates of point A = (r,θ), such that r > 0 and θ < 0.
This problem asks you to identify a positive radial coordinate and a negative angular coordinate for A. Note that A is 3 units from the pole, so r = 3. Furthermore, A lies on the ray that is 45° from the polar axis in the clockwise direction. Recall that angles measured in the clockwise direction have negative measures, so θ = –π/4. Thus, A has polar coordinates (3,–π/4).
The diagram does not tell you that the angle measurement should be negative—it only tells you that the angle between the polar axis and the ray containing A measures π/4. It’s up to you to know that clockwise = negative angle.
Note: In Problems 17.26–17.29, you identify four different points in polar form that coincide with point A, illustrated in Problem 17.26.
17.27 Identify coordinates of point A = (r,θ), such that r > 0 and 0 < θ < 2π.
According to Problem 17.26, A could have angular coordinate θ = –π/4 when r = 3. Add 2π to –π/4 to identify a positive angle coterminal to –π/4.
![]()
Thus, point A has polar coordinates (3,7π/4), as illustrated in the following diagram.

Note: In Problems 17.26–17.29, you identify four different points in polar form that coincide with point A, illustrated in Problem 17.26.
17.28 Identify coordinates of point A = (r,θ), such that r > 0 and 2π < θ < 4π.
According to Problem 17.27, A = (3,7π/4). To identify an angular coordinate for A that is between 2π and 4π, add 2π to the angular coordinate to calculate a positive angle coterminal to 7π/4.
![]()
The polar coordinate pair (3,15π/4) coincides with point A.
Note: In Problems 17.26–17.29, you identify four different points in polar form that coincide with point A, illustrated in Problem 17.26.
17.29 Identify coordinates of point A = (r,θ), such that r < 0 and 0 < θ < 2π.
A ray and its opposite ray form a straight line, which measures 180°, or π radians. Therefore, you can subtract π/4 from π to get 3π/4.
Extend the ray containing point A, and note that it forms a 3π/4 angle with the polar axis. Recall that a negative radial coordinate indicates that you should travel along the opposite ray. Thus, the point (–3,3π/4) is located on the ray opposite θ = 3π/4, on the solid ray in the following diagram.