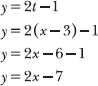Two equations that describe one curve
Note: Problems 17.1–17.4 refer to the curve defined by parametric equations x = t + 3 and y = 2t – 1.
17.1 Identify the point on the curve that corresponds with t = –3.
A parametrically defined graph uses individual equations to represent the coordinates of each point. In this problem, the x- and y-coordinates of each point are defined in terms of a third variable t called the parameter. Substitute t = –3 into both of the parametric equations to identify the coordinates of one point on the graph of the parametric curve.

Thus, the parameter t = –3 corresponds with the rectangular coordinates (x,y) = (0,–7) on the parametric curve.
“Rectangular coordinates” are the coordinates you’ve been using for the entire book, where x represents horizontal distance from the y-axis and y represents vertical distance from the x-axis.
Note: Problems 17.1–17.4 refer to the curve defined by parametric equations x = t + 3 and y = 2t – 1.
17.2 Identify points on the parametric curve by substituting the following values into the parameter: –2, –1, 0, 1, and 2.
Apply the technique demonstrated in Problem 17.1 to substitute the values –2, –1, 0, 1, and 2 into t. In the chart below, each value of t is substituted into both parametric equations, producing a coordinate pair (x,y) that represents a point on the graph of the parametric curve.

Note: Problems 17.1–17.4 refer to the curve defined by parametric equations x = t + 3 and y = 2t – 1.
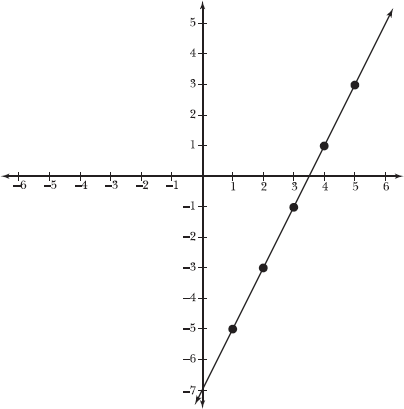
17.3 Graph the parametric curve.
In Problem 17.2, you substitute five values of t into the parametric equations to create five points on the parametric curve: (1,–5), (2,–3), (3,–1), (4,1), and (5,3). As the graph below illustrates, those points trace a linear path.
Can a parametric “curve” be a straight line? Yes. The term “curve” is just a generic way to refer to a parametric graph, no matter how curvy it is or isn’t.
Note that the graph also passes through the point (0,–7) that you identified in Problem 17.1.
Note: Problems 17.1–17.4 refer to the curve defined by parametric equations x = t + 3 and y = 2t – 1.
17.4 Eliminate the parameter to express the parametric curve in rectangular form.
To rewrite a parametric curve in rectangular form, you need to eliminate the parameter, leaving behind only the variables x and y. In this problem, you should solve one of the parametric equations for t and substitute it into the other parametric equation.
If you subtract 3 from both sides of the parametric equation x = t + 3, the result is x – 3 = t. Replace t in the other parametric equation with the equivalent value x – 3.
The parametric equations x = t + 3 and y = 2t – 1 describe the linear equation y = 2x – 7.
Note: Problems 17.5–17.7 refer to the curve defined by parametric equations x = t2 – 3 and y = 4 – t.
17.5 Identify points on the parametric curve by substituting the following values into the parameter: –2, –1, 0, 1, and 2.
This problem asks you to generate a table of values, substituting t = –2, –1, 0, 1, and 2 into the parametric equations to produce points on the graph.

The curve passes through points (1,6), (–2,5), (–3,4), (–2,3), and (1,2).
Note: Problems 17.5–17.7 refer to the curve defined by parametric equations x = t2 – 3 and y = 4 – t.
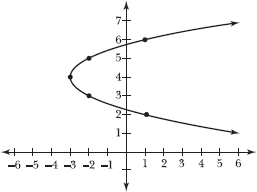
17.6 Graph the curve.
According to Problem 17.5, the curve passes through points (1,6), (–2,5), (–3,4), (–2,3), and (1,2).
Note: Problems 17.5–17.7 refer to the curve defined by parametric equations x = t2 – 3 and y = 4 – t.
17.7 Rewrite the parametrically defined curve in rectangular form.
Solve the parametric equation y = 4 – t for the parameter.

Substitute t = 4 – y into the parametric equation x = t2 – 3 and solve for x to create a function in terms of y.
You could also solve the equation for y to create functions in terms of x, but that’s more complicated. You have to use a technique called completing the square. See Problem 17.10 for more information.
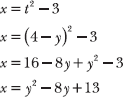
Note: Problems 17.8–17.10 refer to the curve defined by parametric equations x = t2 + 2t and y = t2 – t.
17.8 Identify points on the parametric curve by substituting the following values into the parameter: –2, –1, 0, 1, and 2.
Generate a table of values by substituting t = –2, –1, 0, 1, and 2 into the parametric equations to identify coordinates of points on the curve.
If a problem doesn’t give you values of t, these numbers (–2, –1, 0, 1, and 2) are good values to start with. You can always use more values of t if the shape of the graph isn’t obvious.
Note: Problems 17.8–17.10 refer to the curve defined by parametric equations x = t2 + 2t and y = t2 – t.
17.9 Plot the curve.
According to Problem 17.8, the curve passes through points (0,6), (–1,2), (0,0), (3,0), and (8,2). Although the parametric equations that define the curve are simple quadratics, the resulting parabolic curve has an axis of symmetry that is neither horizontal nor vertical. This produces a graph that appears to be rotated in the coordinate plane.
In other words, the parabola doesn’t open straight up, down, left, or right. Instead, it opens in the upper-right direction.

As this example illustrates, parametric equations can produce very complex curves—curves that are far more difficult to describe in rectangular form, as you discover in Problem 17.10.
Note: Problems 17.8–17.10 refer to the curve defined by parametric equations x = t2 + 2t and y = t2 – t.
17.10 Rewrite the parametrically defined curve in rectangular form.

In order to eliminate the parameter t, you need to solve one of the parametric equations for either x or y. This requires you to complete the square. Begin by adding 1 to both sides of the equation x = t2 + 2t.
It isn’t hard to complete the square, but it’s not something you do very often. If you need to review the technique, see Problems 14.12–14.19 in The Humongous Book of Algebra Problems.
x + 1 = t2 + 2t + 1
Rewrite the right side of the equation as a perfect square.
x + 1 = (t + 1)2
Solve for t.

The parameter t is equivalent to two different expressions in terms of x: ![]() and
and ![]() Substitute each into the parametric equation y = t2 – t.
Substitute each into the parametric equation y = t2 – t.

The rectangular form of the parametric curve is ![]()
Note: Problems 17.11–17.12 refer to the curve defined by parametric equations x = cos θ and y = sin θ.
17.11 Graph the parametric curve.
The parametric equations in this problem contain parameter θ instead of t. Furthermore, the parameter is substituted into a pair of trigonometric equations. Therefore, you should substitute angles from the unit circle into the parameter (such as θ = π/4 and θ = π/2) rather than integers (such as t = –2, –1, 0, 1, and 2). In the following table of values, unit circle angles in (and bounding) the first quadrant are substituted into x = cos θ and y = sin θ.
Each angle θ produces the corresponding coordinate (cos θ,sin θ) on the unit circle. For example, parameter θ = π/4 produces point ![]() Thus, the graph of the parametric curve is the unit circle.
Thus, the graph of the parametric curve is the unit circle.

Note: Problems 17.11–17.12 refer to the curve defined by parametric equations x = cos θ and y = sin θ.
17.12 Rewrite the parametrically defined curve in rectangular form.
According to a Pythagorean identity, cos2 θ + sin2 θ = 1. The parametric equations state that x = cos θ and y = sin θ, so replace cos θ and sin θ in the Pythagorean identity with x and y, respectively.

The parametric curve has rectangular form x2 + y2 = 1.
Note: Problems 17.13–17.14 refer to the curve defined by parametric equations x = 2cosθ and y = 5sinθ.
17.13 Based on the graph you generated in Problem 17.11, sketch the curve without using a table of values.
Each of the points on this parametric curve, when compared to the points on the unit circle, is 2 times as far from the origin horizontally and 5 times as far from the origin vertically. Whereas the unit circle had a leftmost point of (–1,0) and a rightmost point of (1,0), this parametric curve will stretch twice as far, from point (–2,0) to point (2,0). Similarly, whereas the unit circle has a maximum height of 1 and a minimum height of –1, this parametric curve will have a maximum height of 5 and a minimum height of –5.
Because x = 2 cos θ is twice as large as x = cos θ, and y = 5 sin θ is 5 times as large as y = sin θ.

Note: Problems 17.13–17.14 refer to the curve defined by parametric equations x = 2cosθ and y = 5sinθ.
17.14 Rewrite the parametrically defined curve in rectangular form.
Solve x = 2cosθ for cos θ and solve y = 5sin θ for sin θ.

Substitute x/2 for cos θ and y/5 for sin θ in the Pythagorean identity cos2 θ + sin2 θ = 1.

If you wish to eliminate the fractions from the equation x2/4 + y2/25 = 1, multiply each term by the least common denominator: 100.