With squares come Pythagorean identities
Note: Problems 11.23–11.24 refer to the equation cos x = sin x + 1.
11.23 Square both sides of the equation and apply a Pythagorean identity to identify three potential solutions on the interval 0 ≤ x < 2π.
When you square both sides of an equation, you run the risk of introducing extra “solutions” that are actually false. That’s true here, and you’ll pluck out that false “solution” in Problem 11.24.
Square both sides of the equation, as directed by the problem. Note that (sin x + 1)2 ≠ sin2 x + 12.

This equation contains two trigonometric expressions. Apply the technique demonstrated in Problems 11.15–11.22 to rewrite the equation in terms of a single trigonometric expression.
In other words, use a Pythagorean identity. Look for the trig expression that is NOT squared (2 sin x in this equation) and write everything in terms of that trig expression. To get rid of cos2 x here, you use the modified Pythagorean identity cos2 x = 1 – sin2 x.

Factor the quadratic expression.
0 = 2 sin x (sin x + 1)
Apply the zero-product property to identify the solutions on the interval 0 ≤ x < 2π.
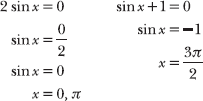
The three potential solutions to this equation are x = 0, x = π, and x = 3π/2.
Note: Problems 11.23–11.24 refer to the equation cos x = sin x + 1.
11.24 Test each of the potential solutions you calculated in Problem 11.23 to identify the actual solutions to the equation on the interval 0 ≤ x < 2π.
According to Problem 11.23, the three potential solutions to the equation are x = 0, x = π, and x = 3π/2. Substitute each into the original equation (cos x = sin x + 1) to determine which, if any, satisfy the equation.
The potential solution x = π does not satisfy the equation. You conclude that the equation cos x = sin x + 1 has two solutions on the interval 0 ≤ x < 2π: x = 0 and x = 3π/2.
Note: Problems 11.25–11.26 refer to the equation sec x – 1 – tan x = tan x.
11.25 Square both sides of the equation and apply a Pythagorean identity to identify potential solutions on the interval 0 ≤ x < π.
Before you square both sides of the equation, add tan x to both sides and combine like terms.
sec x – 1 = 2 tan x
Now square both sides of the equation, noting that (sec x – 1)2 is a simpler expression than (sec x – 1 – tan x)2, the left side of the original equation.

Apply the modified trigonometric identity tan2 x = sec2 x – 1 to rewrite the equation in terms of secant. Combine like terms and factor.

Apply the zero-product property to identify potential solutions to the equation. Notice that the problem directs you to identify solutions on the interval 0 ≤ x < π, which is the range of arccosine. Thus, you should apply the arccosine function to identify the exact solution for both of the following equations.

The potential solutions to the equation sec x – 1 – tan x = tan x are x = 0 and x = arccos (–3/5).
Note: Problems 11.25–11.26 refer to the equation sec x – 1 – tan x = tan x.
11.26 Test each of the potential solutions you calculated in Problem 11.25 to identify the actual solution(s) to the equation on the interval 0 ≤ x < π.
According to Problem 11.25, the two potential solutions are x = 0 and x = arccos (–3/5). Begin by testing the solution x = 0.
sec 0 – 1 – tan 0 = tan 0
Note that sec 0 does not exist. Secant and cosine are reciprocal identities, and sec 0 = cos (1/0) is undefined. As further evidence that sec 0 does not exist, refer to the graph of y = sec x, which has a vertical asymptote at x = 0.
Now determine whether or not x = arccos (–3/5) is a solution to the equation, noting that secant and cosine are reciprocal functions; sec [arccos (–3/5)] = –5/3. Furthermore, tan [arccos (–3/5)] = –4/3.
If x = arccos (–3/5), then x = arcsec (–5/3). Because secant and arcsecant are inverse functions, they cancel each other out: sec [arcsec (–5/3)] = –5/3.
If x = arccos (–3/5), then x is an angle in the second quadrant. Cosine = adjacent/hypotenuse, so you can draw a reference triangle with a horizontal signed length of –3 and a hypotenuse of length 5. That means the vertical side has length +4.

If x = arccos (–3/5), then tan x = opposite/adjacent = +4/–3.

The only solution on the interval 0 ≤ x < π that satisfies the equation sec x – 1 – tan x = tan x is x = arccos (–3/5).
Note: Problems 11.27–11.28 present two different ways to solve the equation cot x = csc x. In each problem, identify all solutions on the interval 0 ≤ x < 2π.
11.27 Rewrite the equation in terms of sine and cosine, and solve the resulting rational equation.
Recall that cot x = cos x/sin x and csc x = 1/sin x.

Subtract 1/sin x from both sides of the equation and combine the fractions, noting that they have common denominator sin x.

A fraction is equal to 0 when its numerator is equal to 0.

Although x = 0 is a potential solution, the original equation contains terms cos x/sin x and 1/sin x, and both of the terms are undefined when x = 0. Thus, there are no real solutions to this equation.
The denominators (sin x) equal 0 when x = 0, and you can’t divide by 0.
Note: Problems 11.27–11.28 present two different ways to solve the equation cot x = csc x. In each problem, identify all solutions on the interval 0 ≤ x < 2π.
11.28 Verify your answer to Problem 11.27 by squaring both sides of the equation and applying a Pythagorean identity.
Square both sides of the equation and recall that 1 + cot2 x = csc2 x.
![]()
Subtract cot2 x from both sides of the equation.
0 = 1
The statement 0 = 1 is untrue, so there are no solutions to this—or the original—equation. This verifies the answer to Problem 11.27, which concluded that no real solutions exist.


