Unit Vectors
Vectors with a magnitude of 1
14.37 Describe the relationship between a vector v and its unit vector ![]() .
.
Given a vector v, the corresponding unit vector ![]() has the same direction as v with a magnitude of 1.
has the same direction as v with a magnitude of 1.
Just like a unit circle has a radius of 1, a unit vector has a length of 1.
Note: In Problems 14.38–14.39, v = <4, 3>.
14.38 Given v = <4,3>, express its unit vector ![]() in component form.
in component form.
Begin by calculating the magnitude of v.

To compute the unit vector, apply this formula: ![]() . In other words, divide each component of v by the magnitude of v.
. In other words, divide each component of v by the magnitude of v.

Note: In Problems 14.38–14.39, v = <4, 3>.
14.39 Verify that the unit vector ![]() identified in Problem 14.38 has a magnitude of 1.
identified in Problem 14.38 has a magnitude of 1.
According to problem 14.38, ![]() . Apply the magnitude formula.
. Apply the magnitude formula.
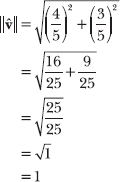
14.40 Given w = <–2, –5>, express the corresponding unit vector ![]() in component form.
in component form.
Begin by calculating the magnitude of w.

Divide each of the components of w by the magnitude of the vector and rationalize the denominators.
Unless your instructor doesn’t mind square roots in the denominator

The standard unit vectors i and j (which may also be written ![]() and
and ![]() or
or ![]() and
and ![]() ) represent unit vectors in the horizontal and vertical directions, respectively. In other words, i is a horizontal vector with length 1 and j is a vertical vector with length 1. In component form, i = <1, 0> and j = <0, 1>.
) represent unit vectors in the horizontal and vertical directions, respectively. In other words, i is a horizontal vector with length 1 and j is a vertical vector with length 1. In component form, i = <1, 0> and j = <0, 1>.
14.42 Write vector v = <8, 3> in terms of standard unit vectors.
In standard positition, v stretches from the origin to the point (8,3). It moves a total of 8 units to the right and 3 units up. Each of those units in the horizontal and vertical directions can be represented by individual unit vectors: 8 horizontal vectors i and 3 vertical vectors j.
v = 8i + 3j
If a vector is in component form <a, b>, you can write it in terms of standard unit vectors by multiplying the x-component by i, multiplying the y-component by j, and then adding those products together.
<a, b> = ai + bj
14.43 Write vector ![]() in terms of standard unit vectors.
in terms of standard unit vectors.
Apply the technique described in Problem 14.42: Multiply the horizontal component by the standard unit vector i = <1, 0>, multiply the vertical component by the standard unit vector j = <0, 1>, and add the products.

Note: In Problems 14.44–14.45, r = <1, 1> and s = <4, 4>.
14.44 Identify the direction in which r travels by graphing it in standard position and calculating its direction angle, the measure of the acute angle it forms with the positive x-axis.
Consider the diagram below, in which r is the hypotenuse of a right triangle. The horizontal and vertical legs of the triangle are, respectively, the x- and y-components of r. In other words, both legs have a length of 1.

Recall that the tangent value of an angle in a right triangle is equal to the length of the side opposite that angle divided by the length of the side adjacent to that angle. Use this trigonometric ratio to calculate θ.

You conclude that r has a direction of 45°, measured counterclockwise from the positive x-axis when r is in standard position.
More simply, the vector has a direction angle of 45°.
Note: In Problems 14.44–14.45, r = <1, 1> and s = <4, 4>.
14.45 Verify that s has the same direction angle as r.
In the diagram below, s is plotted in standard position, forming the hypotenuse of a right triangle whose legs have a length of 4.

Apply the technique described in Problem 14.44; use the tangent ratio to calculate the measure of θ.

You conclude that s, like r, has a direction angle of 45°.
14.46 Based on your answers to Problems 14.44–14.45, identify a vector that has the same direction as v = <a, b>.
Vectors r and s in Problems 14.44–14.45 have the same direction angle: 45°. In fact, all vectors in the first quadrant with equal x- and y-components have direction angle 45°.
If you multiply both components of a vector by the same positive real number, the result is a vector in the same direction. In this case, multiplying each of the components of r = <1, 1> by 4 produces the vector s = <4, 4> in the same direction as r. Therefore, if you multiply the components of v = <a, b> by a positive real number c, then vector <ac, bc> has the same direction as v.
If c is negative, then <ac, bc> and v travel in opposite directions.
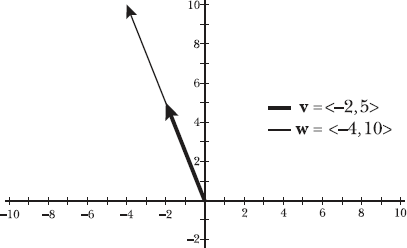
14.47 Explain why v = <–2, 5> and w = <–4, 10> have the same direction and visually verify your answer by plotting both vectors on the same coordinate plane.
According to Problem 14.46, multiplying both components of a vector by the same positive real number produces a vector in the same direction. In this case, multiplying the components of v by 2 generates w.
<(–2)(2), (5)(2)> = <–4, 10>
Plot v and w to visually verify that the vectors have the same direction. In the diagram below, the shorter vector v overlaps longer vector w, so both vectors have the same direction.
Note: In Problems 14.48–14.49, v = <12, –5>.
14.48 Create a vector of length 2 that has the same direction as v = <12, –5>.
Begin by calculating ![]() , a unit vector in the same direction as v. Apply the technique described in Problems 14.38 and 14.40, which requires that you first compute the magnitude of the vector.
, a unit vector in the same direction as v. Apply the technique described in Problems 14.38 and 14.40, which requires that you first compute the magnitude of the vector.
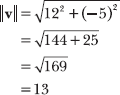
Divide each component of v by the magnitude to identify the unit vector in the same direction as v.
![]()
Now that you have identified a unit vector with the same direction as v, you need to identify a vector in that direction with a length of 2. Simply multiply each component of by the desired magnitude, in this case 2.
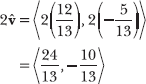
Remember, multiplying both components of a vector by a positive real number produces a vector in the same direction as the original vector, so <24/13, –10/13> has the same direction as v and ![]()
Note: In Problems 14.48–14.49, v = <12, –5>.
14.49 Verify that the vector you identified in Problem 14.48 has a magnitude of 2.
According to Problem 14.48, <24/13, –10/13> has a magnitude of 2. Apply the magnitude formula to verify this claim.

169 · 4 = 676
Calculate the magnitude of w.

Divide each component of w by its magnitude to identify the unit vector ![]() in the same direction as w.
in the same direction as w.
![]()
You are directed to identify a vector in the same direction with a magnitude of 6. Thus, you should multiply both components of the unit vector by 6 to complete the problem.
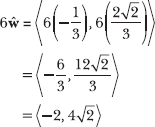
14.51 Create a vector of length d that has the same direction as v = <a, b>.
This is just like Problems 14.48 and 14.50, but you’re using variables instead of numbers.
Begin by calculating the magnitude of v.
![]()
Divide each component of v by its magnitude to identify a unit vector ![]() in the same direction as v.
in the same direction as v.
![]()
You are instructed to create a vector of length d, so multiply each of the components by that constant.
