Scalar Multiplication
Calculate c <a, b>
15.21 Express c<a,b> in component form, assuming a, b, and c are real numbers.
The vector <a,b> is multiplied by a real number c; that real number is called a scalar. To multiply a vector in component form by a scalar value, multiply each of the components by the scalar. In this example, multiply both a and b by c.
A vector has a value (magnitude) and a direction. A scalar only has a value. However, that value changes the SCALE of the vector. For example, multiplying a vector by the scalar 2 doubles its length.
c<a,b> = <ca, cb>
15.22 Express the vector in component form: 3<4,7>.
Multiply each of the components of vector <4,7> by 3.
![]()
Distribute –5 to each of the components of the vector.
![]()
Note: In Problems 15.24–15.27, v = <2,1>.
15.24 Calculate ![]() .
.
Apply the vector magnitude formula presented in Problem 14.25.

Note: In Problems 15.24–15.27, v = <2,1>.
15.25 Express 4v in component form.
Multiply the x- and y-components of v by the scalar 4.
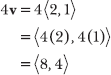
Note: In Problems 15.24–15.27, v = <2,1>.
15.26 Based on your answers to Problems 15.24–15.25, explain how scalar multiplication affects the magnitude of a vector.
In Problem 15.24, you determine that the magnitude of v is ![]() in Problem 15.25, you determine that 4v = <8,4>. Calculate the magnitude of 4v and compare it to the magnitude of v.
in Problem 15.25, you determine that 4v = <8,4>. Calculate the magnitude of 4v and compare it to the magnitude of v.
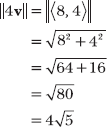
Vector 4v has magnitude ![]() which is 4 times the magnitude of v:
which is 4 times the magnitude of v: ![]() This demonstrates one property of scalar multiplication: The product of a scalar and a vector’s magnitude is equal to the magnitude of the product of the scalar and the vector.
This demonstrates one property of scalar multiplication: The product of a scalar and a vector’s magnitude is equal to the magnitude of the product of the scalar and the vector.
In this problem, four times the length of v is equal to the length of vector 4v.
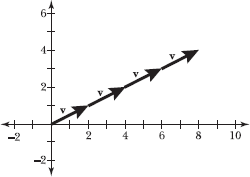
Note that 4v = v + v + v + v. Use the head-to-tail technique demonstrated in Problems 15.1–15.11 to add those four vectors together. As the following diagram illustrates, the sum is a vector whose length must be four times the length of v, because it is literally comprised of four copies of that vector.
15.28 Prove that multiplying v = <a,b> by the scalar c creates a vector with c times the magnitude of v.
This problem asks you to verify that ![]() . In Problems 15.24–15.27, you verify this is true for a specific vector and a specific scalar (<2,1> and 4, respectively); in this problem you prove that the same relationship between magnitude and scalar multiplication holds true for all vectors and scalars. Apply the magnitude formula to both sides of the equation
. In Problems 15.24–15.27, you verify this is true for a specific vector and a specific scalar (<2,1> and 4, respectively); in this problem you prove that the same relationship between magnitude and scalar multiplication holds true for all vectors and scalars. Apply the magnitude formula to both sides of the equation ![]() .
.
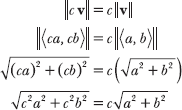
Factor c2 out of both terms on the left side of the equation and simplify the radical expression.

Multiplying v = <a,b> by the scalar c creates a vector with length ![]() , which is c times the length of v.
, which is c times the length of v.
Multiply the components of u by 2, multiply the components of v by 3, and add the vectors.
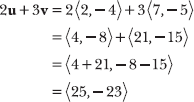
Note: In Problems 15.29–15.31, u = <2,–4> and v = <7,–5>.
15.30 Calculate ![]() .
.
Multiply the components of v by 4, multiply the components of u by 1/2, and subtract the vectors.
Or you could multiply the components of u by –1/2 and add them to 4v.
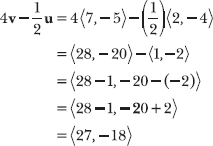
Note: In Problems 15.29–15.31, u = <2,–4> and v = <7,–5>.
15.31 Identify the component form of the unit vector in the direction of w = 4u – v.
Begin by calculating w.
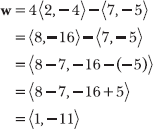
Now calculate the magnitude of w.

According to Problem 14.38, given a vector w, the corresponding unit vector is ![]() . It is equal to the component form of the vector divided by its magnitude.
. It is equal to the component form of the vector divided by its magnitude.

Rationalize the denominators of the components.
Note: In Problems 15.32–15.34, r = <3x,8> and s = <x – 1,5>.
15.32 Calculate 4s – 5r.
Multiply each of the factors by the appropriate scalar values. Note that the x-component of s is x – 1, and both of those terms must be multiplied by 4 when you compute 4s.

Alternative: Instead of multiplying r by –5 and adding 4s + (–5r), you could multiply r by 5 and subtract 5r from 4s.
Note: In Problems 15.32–15.34, r = <3x,8> and s = <x – 1,5>.
15.33 Calculate r – 2s.
When you compute –2s, make sure to distribute –2 to both terms in the x-component: –2(x – 1) = –2x + 2.
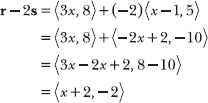
According to Problem 15.33, r – 2s = <x + 2, –2>. Apply the magnitude formula, noting that the magnitude of the vector is equal to ![]()
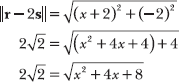
Square both sides of the equation to eliminate the square root symbols.
Squaring both sides could produce extra solutions that aren’t true, so you check the solutions at the end of the problem.

Factor the equation: 0 = x(x + 4). Apply the zero-product property to solve for x.
See Problems 10.12–10.13 to review the zero-product property.
![]()
There are two potential solutions: x = 0 and x = –4. Substitute each into r – 2s = <x + 2, –2> and calculate the magnitude of the resulting vectors to verify that each equals ![]() .
.

You conclude that ![]() when x = 0 or x = –4.
when x = 0 or x = –4.
Multiply the components of w by 6, multiply the components of v by –7, and combine the vectors.

Note: In Problems 15.35–15.36, v = <–3,–2y> and w = <–5,4 – 3y>.
15.36 Given A = (–5,11) and B = (–14,–3), and assuming 6w – 7v is equivalent to ![]() ,calculate y.
,calculate y.
Equivalent vectors have the same component form, so begin by expressing ![]() in terms of its components.
in terms of its components.
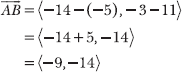
According to Problem 15.35, 6w – 7v = <–9,24 – 4y>. Note that its x-component is already equal to the x-component of ![]() . In order for the vectors to be equivalent, the y-components must be equal as well.
. In order for the vectors to be equivalent, the y-components must be equal as well.

