Law of Cosines
Given SAS or SSS
13.13 State the law of cosines, given a triangle ABC such that a is the length of the side opposite angle A, b is the length of the side opposite angle B, and c is the length of the side opposite angle C.
The law of cosines takes one of three forms, based on the information you are given in the problem. In each case, the square of the length of one side is equal to the sum of the squares of the other side lengths minus double the product of those lengths multiplied by the cosine of the angle opposite the original side.
Added bonus: There is no ambiguous case for the law of cosines. If the formula produces an answer, you can be sure that answer is correct.
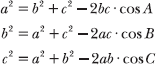
Problems 13.14–13.17 refer to triangle ABC, illustrated below.
13.14 Explain why you must begin this problem with the law of cosines, not the law of sines.
The law of cosines is usually applied to triangles in which you are given the lengths of two sides and an included angle (side-angle-side or SAS) or the lengths of all three sides (side-side-side or SSS). In this problem, you are given the length of all three sides.
Problems 13.14–13.17 refer to triangle ABC, illustrated in Problem 13.14.
13.15 Identify the angle measure you should calculate first and explain your answer.
When possible, you should use the law of cosines to calculate the largest angle in a triangle, in case it is obtuse. As Problems 13.9–13.12 explain, the law of sines is unable to differentiate between acute and obtuse angles; the law of cosines does not suffer this limitation. The largest angle in a triangle is always opposite the longest side. Because the longest side of this triangle is b = 9, you should apply the law of cosines to calculate the measure of angle B.
Because the restricted range of arccosine is 
it can calculate acute angles (whose measures are greater than 0° but less than 90°) and obtuse angles (whose measures are greater than 90° but less than 180°).
Problems 13.14–13.17 refer to triangle ABC, illustrated in Problem 13.14.
13.16 Calculate the angle you identified in Problem 13.15, and report the answer accurate to the thousandths place.
As Problem 13.15 explains, you should calculate the measure of angle B first. Use the version of the law of cosines that includes B.
If the cosine is negative, the angle is obtuse. If the cosine is positive, the angle is acute.
The measure of angle B is approximately 127.169°.
Problems 13.14–13.17 refer to triangle ABC, illustrated in Problem 13.14.
13.17 Calculate the measures of the remaining angles in triangle ABC, accurate to the thousandths place.
According to Problem 13.16, angle B measures approximately 127.1688997°; the opposite side has length b = 9. Although you can apply the law of cosines to calculate another angle measure in the triangle, you should apply the law of sines instead, because it requires less arithmetic to complete. Furthermore, because you have already calculated the measure of the largest angle in triangle ABC, the ambiguous case is no longer a concern.
You can choose to calculate the measure of angle A or C; below, the law of sines is used to calculate the measure of angle A.
Angle A measures approximately 20.742°. Now that you know two of the angle measures, you can subtract them from 180° to identify the remaining angle measure in the triangle. Use the unrounded angle measurements to avoid possible rounding errors.
Problems 13.18–13.21 refer to triangle XYZ, illustrated below.
13.18 Calculate XZ using the law of cosines, and report your answer accurate to the thousandths place.
The diagram provides the lengths of two sides and the measure of the angle they form, so you are given side-angle-side or SAS; therefore, the law of cosines should be applied to calculate the missing measurement. Note that side 
is opposite angle Y, so y = XZ.
Therefore, XZ θ 4.264.
Problems 13.18–13.21 refer to triangle XYZ, illustrated in Problem 13.18.
13.19 Identify an angle that must be acute and calculate its measure using the law of sines. Report your answer accurate to the thousandths place.
Two side lengths are given in the diagram: XY = 4 and YZ = 8. According to Problem 13.18, XZ ≈ 4.264. The largest angle must be opposite the largest side, so angle X is larger than angles Y and Z. A triangle can have, at most, one obtuse angle. In this case, only angle X could be obtuse; thus, angle Z must be acute.
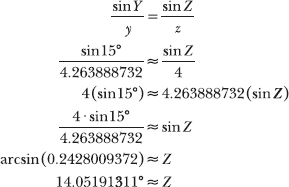
Angle Z measures approximately 14.052°.
Problems 13.18–13.21 refer to triangle XYZ, illustrated in Problem 13.18.
13.20 Calculate the measure of the remaining angle, accurate to the thousandths place.
The diagram states that angle Y measures 15°; according to Problem 13.19, angle Z measures approximately 14.05191311°. Subtract these values from 180° to identify the measure of angle X.
Angle X measures approximately 150.948°.
Problems 13.18–13.21 refer to triangle XYZ, illustrated in Problem 13.18.
13.21 Verify your answer to Problem 13.20 using the law of cosines.
Apply the law of cosines to calculate the measure of angle X, given the lengths of the sides of the triangle: x = 8, y ≈ 4.263888732, and z = 4.
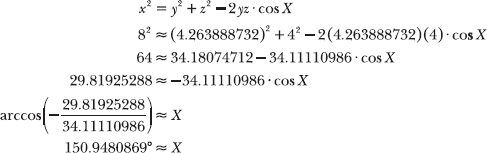
Problems 13.22–13.24 refer to triangle LMN, illustrated below.
13.22 Calculate the area of triangle LMN using only the information given in the diagram, and report your answer accurate to the thousandths place.
You are given the lengths of two sides and the measure of the included angle (SAS); apply the area formula introduced in Problem 12.14.
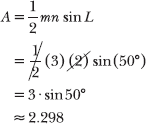
Problems 13.22–13.24 refer to triangle LMN, illustrated in Problem 13.22.
13.23 Calculate MN, and report your answer accurate to the thousandths place.
Given the lengths of two sides of a triangle and the measure of the included angle, you should apply the law of cosines to calculate the length of the side opposite the included angle. Note that l = MN.
Thus, MN ≈ 2.299.
Problems 13.22–13.24 refer to triangle LMN, illustrated in Problem 13.22.
13.24 Verify your answer to Problem 13.22 using Heron’s formula.
Heron’s formula, first introduced in Problem 12.25, allows you to calculate the area of a triangle based on the lengths of its sides. You are given LM = 2 and LN = 3; according to Problem 13.23, MN ≈ 2.299249591. Begin by calculating the semiperimeter, s.
Now apply Heron’s formula to calculate the area A of triangle LMN.
Some calculators use more decimals than they actually show on screen, so the number under your square root may not end in “806” like the book’s does. That’s okay, as long as you still end up with the same answer rounded to the thousandths place: 2.298.
This is the same area value you calculated in Problem 13.22, thus verifying your answer.