Rectangular Form of Complex Numbers
Add, subtract, multiply, divide, and graph
Note: Problems 18.1–18.3 refer to the complex number z = 5 + 3i.
18.1 Identify the real and imaginary parts of z.
A complex number is the sum of two distinct parts, a real number part and an imaginary number part. In this problem, the complex number z = 5 + 3i equals the sum of its real number part 5 and the imaginary part 3 that is multiplied by i. Note that 
; it is considered imaginary because you cannot calculate the square root of a negative number.
The imaginary part is the real number that is multiplied by i. In other words, 3 is the imaginary part of 5 + 3i, not 3i.
Note: Problems 18.1–18.3 refer to the complex number z = 5 + 3i.
18.2 Identify the conjugate of z.
To derive the conjugate of a complex number, change the sign of its imaginary part: 5 – 3i is the conjugate of 5 + 3i.
Note: Problems 18.1–18.3 refer to the complex number z = 5 + 3i.
18.3 Plot z on the complex plane.
The complex plane is similar to the coordinate plane, but the horizontal and vertical axes do not represent x and y. Instead, the horizontal axis represents the real part of the complex number, and the vertical axis represents the imaginary part. The real part of z = 5 + 3i is 5, so z is located 5 units right of the origin. The imaginary part of z is 3, so z is located 3 units above the origin, as illustrated below.
Therefore, z = 5 + 3i has rectangular coordinates (5, 3). More generally, any complex number a + bi has rectangular coordinates (a, b).
To plot a complex point, treat the real part as the x-coordinate and the number multiplied by i as the y-coordinate.
18.4 Given the complex number z1 = –1 + 5i, identify its conjugate z2 and plot z2 in the complex plane.
To calculate the conjugate of z1 = –1 + 5i, change the sign of 5i, the imaginary part: z2 = –1 – 5i. Therefore, z2 is located 1 unit left of, and 5 units below, the origin. The rectangular coordinates of z2 are (–1, –5).
18.5 Simplify the expression: i6.
Recall that 
. Therefore, 
. Rewrite i6 as a series of i2 factors multiplied together.
You conclude that i 6 = –1.
Note: Problems 18.6–18.9 refer to complex numbers c1 = 2 – 3i and c2 = 5 + i.
18.6 Calculate c1 + c2.
To add complex numbers, combine their real and imaginary parts independently.
Note: Problems 18.6–18.9 refer to complex numbers c1 = 2 – 3i and c2 = 5 + i.
18.7 Calculate c1 – c2.
In order to subtract c2 from c1, subtract the real and imaginary parts of c2 from the corresponding parts of c1.
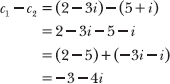
Note: Problems 18.6–18.9 refer to complex numbers c1 = 2 – 3i and c2 = 5 + i.
18.8 Calculate c1 c2.
Apply the FOIL method to multiply complex numbers, the same technique you use to multiply two binomials: (a + b)(c + d) = ac + ad + bc + bd.
Recall that i2 = –1.
Note: Problems 18.6–18.9 refer to complex numbers c1 = 2 – 3i and c2 = 5 + i.
18.9 Calculate c1 ÷ c2.
Begin by writing the quotient as a fraction.
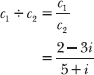
Multiply the numerator and denominator of the fraction by 5 – i, the conjugate of the denominator.
Apply the FOIL method to calculate the product (2 – 3i)(5 – i) in the numerator and the product (5 + i)(5 – i) in the denominator.
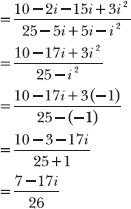
Most instructors require you to express the real and imaginary parts of the quotient as individual values, as demonstrated below.
Divide each term of the numerator 7 – 17i by the denominator 26.
Note: Problems 18.10–18.12 refer to complex numbers z1 = 9 + 4i and z2 = 9 – 4i.
z1 and z2 are conjugates.
18.10 Calculate z1 – z2.
Subtract the real and imaginary parts of z2 from the corresponding parts of z1.
Note: Problems 18.10–18.12 refer to complex numbers z1 = 9 + 4i and z2 = 9 – 4i.
18.11 Calculate z1 z2.
Apply the FOIL method to calculate the product of two complex numbers.
Notice that the product of a complex number and its conjugate is a real number—it contains no imaginary part.
That’s why you multiply by the conjugate when you divide complex numbers. You need to get rid of the complex number in the denominator.
Note: Problems 18.10–18.12 refer to complex numbers z1 = 9 + 4i and z2 = 9 – 4i.
18.12 Calculate z1 ÷ z2.
Express the quotient as a fraction and multiply the numerator and denominator by 9 + 4i, the conjugate of the denominator.
According to Problem 18.11, (9 – 4i) (9 + 4i) = 97.