Graphs that repeat and sort of look like a heartbeat
Problems 5.1–5.5 refer to the graph of periodic function f(x) below.

5.1 Identify the domain of f(x).
The domain of a function is the collection of values for which the function is defined. Given a graph of a function, the most straightforward method to determine its domain is to imagine a series of vertical lines on the coordinate plane. Any vertical line drawn on the plane that intersects the graph represents an x-value for which the function is defined (and, therefore, a value in the domain of the function).
The collection of all the numbers you can plug into the function, usually in place of x or θ.
Consider the graph of f(x) in this problem. If you were to draw a vertical line at x = 1, it would intersect the graph at height y = 3. Therefore, the function is defined at x = 1, and f(1) = 3. In fact, any vertical line drawn on the coordinate plane intersects this graph, so the domain of f(x) is all real numbers.
The correct answer in set notation, if required by your instructor, is “{x | x is a real number}.” Note that the small vertical line between the x’s in set notation is read “such that.” Therefore, you read the answer as “the set of all x, such that x is a real number.” Written in interval notation, the domain is (–∞,∞).
Interval notation indicates a set of possible values between two boundaries. In this case the boundaries are ![]() (the ends of the real number line), so all of the real numbers fall within the boundaries.
(the ends of the real number line), so all of the real numbers fall within the boundaries.
Problems 5.1–5.5 refer to the graph of periodic function f(x) in Problem 5.1.
5.2 Identify the range of f(x).
In Problem 5.1, vertical lines in the coordinate plane help you determine the domain of f(x), the set of possible inputs for a function. Similarly, horizontal lines that intersect the graph of a function represent members of the range—the set of outputs for the function.
Consider the given graph of f(x). If you were to draw a horizontal line along the x-axis, which has equation f(x) = 0 (or y = 0), it would intersect the graph repeatedly. The function has a vertical height of 0 at x = –6, x = –4, x = –3, x = –1, x = 0, x = 2, x = 3, x = 5, and x = 6. Keep in mind that f(x) is a periodic function, so the repetitive pattern of its graph will continue in both the positive and negative directions along the x-axis. It will intersect the graph infinitely many times over the entire domain of f(x).
Horizontal lines as high as f(x) = 3 and as low as f(x) = –1 intersect the graph, but anything outside of those bounds will not. For instance, the horizontal line f(x) = 4 that is 4 units above the x-axis lies a full unit above the peaks of f(x); it does not intersect the graph, so f(x) = 4 does not belong to the domain.
Because the horizontal lines between (and including) f(x) = –1 and f(x) = 3 all intersect the graph, the domain of f(x) is –1 ≤ f(x) ≤ 3. In set notation, the range is {f(x) | –1 ≤ f(x) ≤ 3}, and in interval notation, the solution is [–1,3].
Parentheses in interval notation indicate that the boundaries are excluded, and brackets mean the boundaries are included. For example, [–1,3] means “all the numbers between –1 and 3, INCLUDING –1 and 3.”
Problems 5.1–5.5 refer to the graph of periodic function f(x) in Problem 5.1.
5.3 Identify the minimum and maximum function values of f(x).
Problem 5.2 states that the range of f(x) is –1 ≤ f(x) ≤ 3, because the function has a maximum height of 3 and a minimum height of –1.
Problems 5.1–5.5 refer to the graph of periodic function f(x) in Problem 5.1.
5.4 Calculate the amplitude of f(x).
The “amplitude” of a function is defined as the difference of the function’s maximum and minimum values, divided by two. According to Problem 5.3, those values are 3 and –1, respectively.

Visually, the amplitude of a periodic function represents the distance a function stretches from the horizontal line that is equidistant from the function’s maximum and minimum values—the “middle” of the function, as illustrated below.
Think of the max and min as the top and bottom of a big rectangle that stretches across the graph. If you divide that rectangle in half, the amplitude is the distance from the “middle” to the top and bottom of the rectangle.

Problems 5.1–5.5 refer to the graph of periodic function f(x) in Problem 5.1.
5.5 Calculate the period of f(x).
Recall that a periodic function infinitely repeats the same function values in the coordinate plane. The smallest horizontal distance over which the function does not repeat is called the period of the function. In other words, the period is the number of units, along the x-axis, it takes for the function to repeat itself.
Consider the graph of f(x). It intersects the x-axis at x = 0, rises to a height of 3 at x = 1, returns to the x-axis at x = 2, dips below the x-axis until approximately x = 2.5, and then returns to the x-axis at x = 3. The function repeats the same pattern again between x = 3 and x = 6. In fact, the same pattern is repeated left of the y-axis, between x = –6 and x = –3 and again between x = –3 and x = 0.

The values of f(x) repeat every 3 units along the x-axis, so the period of f(x) is 3. More formally, the period is equal to the difference of two x-values marking the beginning and end of one complete iteration of the graph. For instance, the rightmost full iteration of f(x) begins at x = 3 and ends at x = 6. Therefore, the period is 6 – 3 = 3.
Problems 5.6–5.9 refer to the graph of periodic function g(x) below.
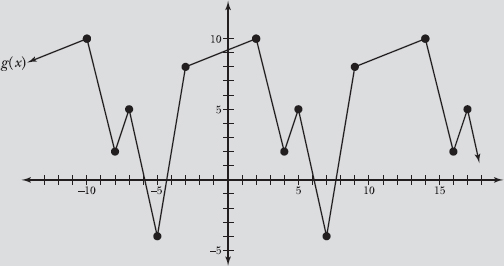
5.6 Identify the domain of g(x).
As Problem 5.1 explains, any vertical line that intersects the graph of g(x) represents a member of the domain. Any vertical line drawn on this coordinate plane will intersect the graph, so the domain of g(x) is all real numbers. In set notation, the domain of g(x) is {x | x is a real number}; in interval notation, the domain is (–∞,∞).
Problems 5.6–5.9 refer to the graph of periodic function g(x) in Problem 5.6.
5.7 Identify the range of g(x).
Different instructors require you to report the answer different ways, so the book lists the three most commonly used formats. You don’t have to use all three—just figure out which your instructor prefers.
The function reaches a maximum height of 10 (at x = –10, x = 2, and x = 14) and a minimum height of –4 (at x = –5 and x = 7). All horizontal lines between g(x) = 10 and g(x) = –4 also intersect the graph, so the range of g(x) is –4 ≤ g(x) ≤ 10. In set notation, the range is {g(x) | –4 ≤ g(x) ≤ 10}, and in interval notation, the range is [–4,10].
Problems 5.6–5.9 refer to the graph of periodic function g(x) in Problem 5.6.
5.8 Calculate the amplitude of g(x).
According to Problem 5.7, the maximum and minimum values of g(x) are 10 and –4, respectively. Substitute these values into the amplitude formula presented in Problem 5.4.

Problems 5.6–5.9 refer to the graph of periodic function g(x) in Problem 5.6.
5.9 Calculate the period of g(x).
To identify the period, locate points on the graph that have the same height and determine whether or not they represent a point after which the graph repeats. For example, the graph of g(x) reaches its maximum height at x = 2 and again at x = 14. In both cases, the graph immediately drops to a height of g(x) = 2 exactly 2 units to the right: g(4) = g(16) = 2. The pattern is further confirmed when you move 1 unit to the right; both graphs jump 3 units higher: g(5) = g(17) = 5.
In the following diagram, one period of g(x) is shaded, representing the horizontal distance between two points at which g(x) reaches its maximum value. You are not required to use the maximum values of a periodic graph to mark the “beginning” and “end” of one period. You may choose to mark the beginning and end of a period using any two corresponding points, such as minimum points or x-intercepts, and your final answer will be the same.
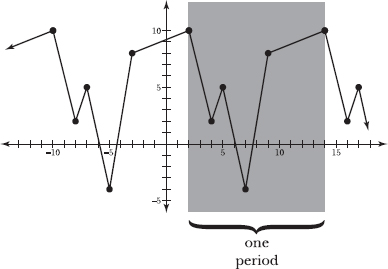
One period of g(x) is bounded on the left by the vertical line x = 2 and is bounded on the right by the vertical line x = 14. The period is equal to the difference between these x values.
![]()
Note: Problems 5.10–5.12 refer to the graph of periodic function h(x) below.

5.10 Identify the domain and range of h(x) on the interval –2π ≤ x ≤ 2π.
The graph has vertical asymptotes at x = –π and x = π, so vertical lines drawn at these x-values will not intersect the graph. Whereas h(x) gets infinitely close to the asymptotes as you approach those dotted vertical lines from the right and the left, the graph never actually intersects them. Hence, the graph is undefined at x = –π and x = π. The domain of h(x) is all real numbers, excluding –π and π. In set notation, the domain is {x | x is a real number such that –2π ≤ x ≤ 2π, x ≠ –π, and x ≠ π}. In interval notation, the domain is ![]() .
.
Asymptotes are lines that a function approaches but never reaches; they are usually drawn as dotted lines. While they are not technically part of the function, they definitely shape its graph.
The problem only asks you to identify the domain for the portion of h(x) displayed in this diagram (–2π ≤ x ≤ 2π), but h(x) is periodic. All of the function values (and the undefined values) will repeat infinitely.
Horizontal lines drawn on the coordinate plane will intersect h(x) at and above the x-axis, so the range of h(x) is all real numbers greater than or equal to 0. In set notation, the range is {h(x) | h(x) ≥ 0}. In interval notation, the range is [0,∞).
Note: Problems 5.10–5.12 refer to the graph of periodic function h(x) in Problem 5.10.
5.11 Calculate the amplitude of h(x).
The minimum value of the function is h(x) = 0, but the function has no finite maximum value. Its graph increases without bound as it approaches the vertical asymptotes. Therefore, amplitude is not defined for h(x).
Note: Problems 5.10–5.12 refer to the graph of periodic function h(x) in Problem 5.10.
5.12 Calculate the period of h(x).
One full period of the graph occurs between x = –π and x = π. To compute the period, calculate the difference of the x-values.

Remember, h(x) is undefined at ![]() , at the asymptote. If you add the period
, at the asymptote. If you add the period ![]() to (or subtract it from) that undefined x-value, you get other x-values at which h(x) is undefined. For example,
to (or subtract it from) that undefined x-value, you get other x-values at which h(x) is undefined. For example, ![]() , so h(x) is also undefined at
, so h(x) is also undefined at ![]() .
.
