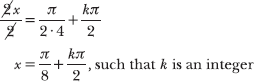Functions of Multiple Angles

Instead of cos x = 1, solve cos 5x = 1

Subtract 1 from both sides of the equation to isolate sin x left of the equal sign.

sin x = –1

Taking the arcsine of both sides of this equation solves it for x.

x = arcsin (–1)

Note that the range of arcsine is –π/2 ≤ arcsin x ≤ π/2, so if you were asked to supply the exact solution to this equation, the answer would be x = –π/2. However, the problem directs you to identify all solutions within a single rotation on the coordinate plane. The only angle on this interval with a sine value of –1 is x = 3π/2. (Note that –π/2 and 3π/2 are coterminal angles, and the choice of one angle versus the other in the solution is dictated solely by the interval specified in the problem.)

In other words, the angles between 0 and 2π including 0 but excluding 2π

This equation is similar to the equation in Problem 10.33 (sin x + 1 = 0); only the arguments of the equations differ. This equation contains argument 2x, a double angle. Regardless of this difference, you still begin by isolating the trigonometric function on one side of the equal sign. In other words, you still begin by subtracting 1 from both sides of the equation.

sin 2x = –1

Now apply the arcsine function to both sides of the equation.

2x = arcsin (–1)

As Problem 10.33 states, angle 3π/2 has a sine value of –1, but because this equation contains a double angle (2x instead of x), you should list twice as many solutions. Thus, you should calculate a coterminal angle for the solution 3π/2 by adding the period of sine (2π).

Rewrite the equation 2x = arcsin (–1), replacing arcsin (–1) with the two solutions you have identified.

To finish solving the equation, you must isolate x. Eliminate its coefficient (2) by multiplying both sides of the equation by 1/2.

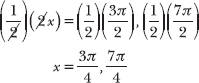
Note that both of the final solutions belong to the interval specified by the problem: 0 ≤ 3π/4 < 7π/4 < 2π.

Remember to adjust the total number of solutions based on the coefficient of x, especially when the problem asks you to list the solutions on the interval 0 ≤ x < 2π.

In Problem 10.34, the trig expression contained 2x and you had to list 2 times as many solutions. In this problem, the trig expression contains 3x, so you will need to list 3 times as many solutions.

Like Problems 10.33–10.34, you begin this problem by subtracting 1 from both sides of the equation. In order to solve any trigonometric equation, you must isolate the expression containing the variable (in this case sin 3x) on one side of the equation.

sin 3x = –1

Apply the arcsine function to eliminate the sine expression containing x, the variable for which you are solving.

3x = arcsin (–1)

Only one angle on the unit circle has a sine value of –1: x = 3π/2. However, the coefficient of x is 3, so you must list three solutions—three times as many as the single solution 3π/2. Add 2π to 3π/2 (like you did in Problem 10.34) to identify coterminal angle x = 7π/2, and then add 2π to that angle in order identify a second coterminal angle.

Return to the equation 3x = arcsin (–1) and replace the arcsine expression with the three angles you have identified.

Multiply both sides of the equation by 1/3 to solve for x.

Problem 10.35 states that equation sin 3x + 1 = 0 has three solutions that lie between 0 and 2π: x = π/2, 7π/6, and 11π/6. Substitute each into the equation to verify that the resulting statements are true.

In Problem 10.35, you calculated two angles coterminal to If the angles are coterminal, then all three have the same sine value: –1.

In order to solve for x, you must first eliminate the trigonometric equation that contains the variable. Take the arcsine of both sides of the equation.

2x = arcsin 0

Only angles 0 and π have a sine value of 0 on the interval 0 ≤ x < 2π. Because x has a coefficient of 2, you should list twice as many solutions—four angles instead of two. Add 2π (the period of sine) to x = 0 and x = π to identify two additional coterminal angles: 0 + 2π = 2π and π + 2π = 3π.

2x = 0, π, 2π, 3π

Divide by 2 to solve for x.

Take the arccosine of both sides of the equation.

The two angles on the unit circle that have a cosine of are 3π/4 and 5π/4. Calculate two coterminal angles for each, adding 2π and then 4π to 3π/4 and 5π/4.

Multiply each term by 1/3 to solve for x.

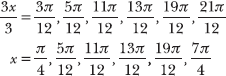
Isolate cos 2x on the left side of the equation and simplify the square root expression.

Take the arccosine of both sides of the equation.

Angles π/4 and 7π/4 have cosine values of , but you should calculate one coterminal angle for each; an x-coefficient of 2 requires twice as many solutions.

Divide by 2 to solve for x.

Simplify both sides of the equation and isolate the trigonometric expression on one side of the equal sign.

To solve the equation cos 3x = –1 on the interval you need to write three times the number of solutions However, for the general solution, don’t bother with the coterminal angles because your solution already includes ALL coterminal angles.

Only angle π has a cosine of –1 on the interval 0 ≤ x < 2π. Because the coefficient of x is 3, you may be tempted to list three times as many solutions, most likely 3π and 5π, which are angles coterminal to π. However, this problem asks for the general solution, which includes all coterminal angles. Therefore, there is no need to list additional solutions based on the coefficient of x.

π + 2kπ = 3x

Divide each term by 3, including 2kπ, to solve for x.

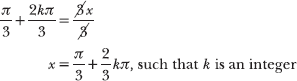
Isolate 2x on one side of the equation.

Consider the full period of tangent lying between θ = –π/2 and θ = π/2. Only angle π/4 has a tangent value of 1 on that interval. Because you are asked to report the general solution, there is no need to list twice as many solutions (despite the fact that x has a coefficient of 2); the general solution will include all coterminal angles.

Solve for x, dividing each term by 2 or multiplying each term by 1/2.

Isolate the trigonometric expression on the left side of the equation and apply the arcsine function.

The two angles on the interval 0 ≤ x < 2π that have a sine value of 1/2 are x = π/6 and 5π/6. Although the coefficient of x is 1/2, you do not apply the technique demonstrated in Problem 10.34; in other words, a coefficient of 1/2 does not imply that you should list half as many solutions. Fractional coefficients between 0 and 1 do not require you to identify additional coterminal solutions.

But you should check to make sure you don’t end up with extra solutions that are outside the specified interval

To solve for x, multiply each of the terms by 2.

Complete the steps outlined in Problem 10.42 to isolate the variable expression x/2 on the left side of the equation, but before you solve for x, list the general form of the solutions.

Solve for x, multiplying each of the terms in the equation by 2.

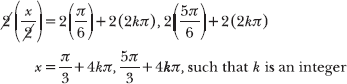
The two smallest positive solutions are π/3 and 5π/3. To generate the next two solutions, substitute k = 1 into each of the expressions.

Thus, the four smallest positive solutions to the equation are .

The left side of the equation is a factorable quadratic expression: 3y² – 5y – 2 = (3y + 1)(y – 2), such that y = sec (x/2).

Check out Problem 10.18 if you need to review factoring and the zero-product property.

Apply the zero-product property, setting each factor equal to 0 and solving the two resulting equations for sec x.

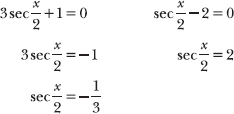
Apply the reciprocal identity cos θ = 1/sec θ and solve for x.

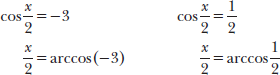
Note that the domain of arccosine (like the range of cosine) is –1 ≤ θ ≤ 1, so arccos (–3) is not defined; this equation may be omitted from the final solution. However, there are two angles with a cosine value of 1/2.

The coefficient of x is 1/2. As Problem 10.42 explains, you do not have to identify additional coterminal angles for fractional coefficients between 0 and 1. Multiply each term by 2 in order to solve for x.

However, one of these solutions will no longer fit in the interval once you solve for x.

Note that 10π/3 is greater than the upper bound of the interval (2π), so the equation has only one valid solution: x = 2π/3.

Subtract 4 from both sides of the equation; the result is a quadratic expression left of the equal sign and the number 0 right of the equal sign.

The quadratic expression cannot be factored, so apply the quadratic formula, as demonstrated in Problem 10.25. Note that the formula is set equal to the trigonometric expression tan (x/3).

The numerator has a greatest common factor of 2. Factor it out of that expression to simplify the fraction.

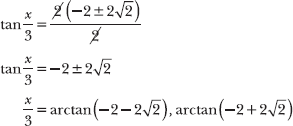
The problem directs you to calculate the general solution, so add multiples of π (the period of tangent) to each solution.

Multiply each term by 3 to solve for x.