Cosine Functions
The sine graph schooched slightly to the left
5.35 Graph f(θ) = cos θ on the interval –2π ≤ θ ≤ 2π.
According to the trigonometric unit circle, cos 0 = cos 2π = 1, cos π/2 = 0, cos π = –1, and cos 3π/2 = 0. The graph of f(θ) = cos θ is very similar to the graph of y = sin θ. In fact, as Problem 5.36 explains, the two graphs are equivalent apart from a simple horizontal shift.

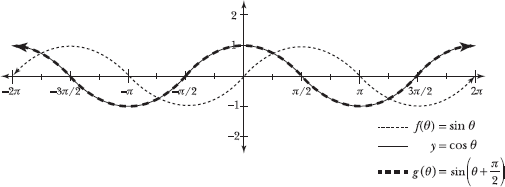
5.36 Graph f(θ) = cos θ and ![]() to visually verify that f(θ) = g(θ).
to visually verify that f(θ) = g(θ).
The graph of g(θ) shifts the graph of y = sin θ a horizontal distance of π/2 units to the left. The resulting graph coincides with the graph of f(θ) = cos θ.
Overlaps
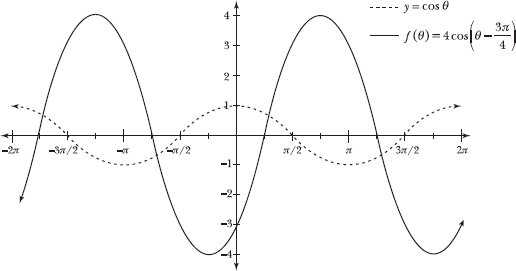
5.37 Graph ![]() .
.
Multiplying the cosine function by 4 stretches its amplitude by a factor of 4. Thus, the graph of f(θ) stretches to a maximum height of 4 and a minimum height of –4. Subtracting 3π/4 from the input of the function shifts the graph 3π/4 units to the right.
Each of the tic marks along the x-axis represents a distance of π/4, so move the graph three tic marks to the right.
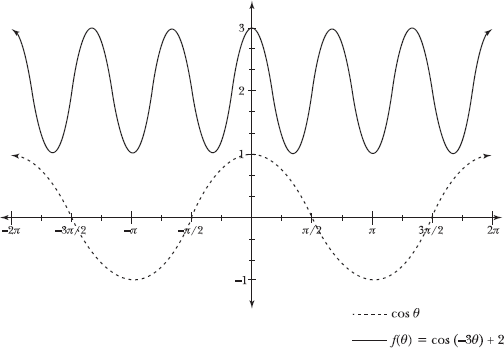
5.38 Graph f(θ) = cos(–3θ) + 2.
When graphing a function using numerous transformations, you should complete them in the following order:
- Horizontal and vertical stretching/compression, which occur when either the function or its input is multiplied by a real number
- Reflections about the x- or y-axes, which occur when either the function or its input is multiplied by –1
- Horizontal and vertical shifts, which occur when a real number is added to (or subtracted from) a function or its input
Technically speaking, the first two steps in the list above may be reversed, but horizontal and vertical shifts must always be completed last.
In this problem, the input of y = cos θ is multiplied by –3, so the graph of y = cos θ is reflected about the y-axis and compressed by a factor of 3. Then, because 2 is added to the function, the graph is shifted upward a distance of 2 units.
The graph of ![]() is “y-symmetric,” because the right and left sides of the graph look like reflections of each other, as if the y-axis were a mirror. When you reflect a y-symmetric graph across the y-axis, it looks exactly the same as it did before you reflected it.
is “y-symmetric,” because the right and left sides of the graph look like reflections of each other, as if the y-axis were a mirror. When you reflect a y-symmetric graph across the y-axis, it looks exactly the same as it did before you reflected it.

Note: Problems 5.39–5.40 explain how to graph ![]() , which contains a specific pair of transformations: a horizontal shift and a period change.
, which contains a specific pair of transformations: a horizontal shift and a period change.
5.39 Calculate the θ-coordinates on the graph of g(θ) that correspond with θ = 0 and θ = 2π on the untransformed graph of y = cos θ.
If you multiply the input of a function by a real number and add a value to (or subtract a value from) the input as well, you have to apply a specific technique to graph this pair of transformations.
In other words, if you graph a function f(x) = cos (Bx + C), where B ≠ 1 and C ≠ 0, then you have to apply this technique. In this problem, B = 1/2 and ![]() .
.
The period of the untransformed graph y = cos θ is 2π. Recall that one full period of cos θ occurs between the horizontal boundaries of θ = 0 and θ = 2π. To locate the starting and ending points of one period on the transformed graph g(θ), set the parenthetical quantity ![]() equal to 0 and 2π and solve for θ.
equal to 0 and 2π and solve for θ.


Note: Problems 5.39–5.40 explain how to graph ![]() , which contains a specific pair of transformations: a horizontal shift and a period change.
, which contains a specific pair of transformations: a horizontal shift and a period change.
5.40 Graph g(θ).
According to Problem 5.39, the period of y = cos θ that normally lies between θ = 0 and θ = 2π lies between θ = 2π and θ = 6π on the transformed graph of g(θ). Note that neither the amplitude of y = cos θ nor its vertical position changes.
Look at the graph of cosine between ![]() Draw that same shape between the new boundaries,
Draw that same shape between the new boundaries, ![]()


Apply the technique described in Problems 5.40–5.41. Because one full period of y = cos θ lies between θ = 0 and θ = 2π, set the parenthetical quantity ![]() equal to both values of θ to identify the values of θ that bound one period of f(θ).
equal to both values of θ to identify the values of θ that bound one period of f(θ).
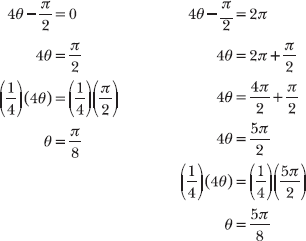
The portion of the untransformed graph y = cos θ that lies between θ = 0 and θ = 2π will lie between θ = π/8 and θ = 5π/8 on the transformed graph of f(θ).
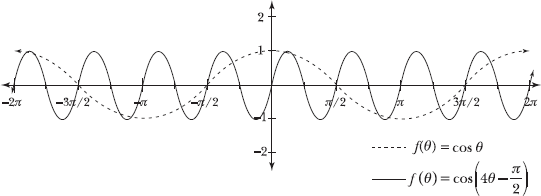
The period of a transformed graph is equal to the absolute value of the original, untransformed period divided by the coefficient of θ.

Note that the difference of the θ-values calculated above is also equal to the period of f(θ).