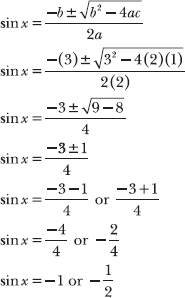Quadratic Formula
When you can’t factor
10.24 Identify the quadratic formula used to solve quadratic equation ax2 + bx + c = 0, such that a, b, and c are integers and a ≠ 0.
The quadratic formula allows you to solve a quadratic equation using only its coefficients. This technique, like the factoring technique described in Problems 10.12–10.23, requires that one side of the equation equals 0.
Substitute a = 2, b = –5, and c = 1 into the quadratic formula, identified in Problem 10.24.
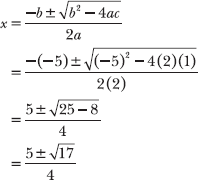
There are two solutions to the equation: 
.
Note: Problems 10.26–10.27 demonstrate two different ways to solve the quadratic trigonometric equation 2 sin2 x + 3 sin x + 1 = 0. Identify all solutions on the interval 0 ≤ x < 2 π.
10.26 Solve the equation by factoring.
Apply the technique described in Problems 10.12–10.23, factoring the expression and then setting each factor equal to zero, applying the zero-product property.
The solution is 
.
Note: Problems 10.26–10.27 demonstrate two different ways to solve the quadratic trigonometric equation 2 sin2 x + 3 sin x + 1 = 0. Identify all solutions on the interval 0 ≤ x < 2π.
10.27 Verify the solutions you identified in Problem 10.26 by applying the quadratic formula.
Substitute a = 2, b = 3, and c = 1 into the quadratic formula. Note that the left side of the equation in the traditional quadratic formula is simply “x,” but in this problem, the left side of the equation is “sin x.”
Thus, sin x = –1 or sin x = –1/2. These are the same equations produced by the zero-product property in Problem 10.26, so the solutions are the same: x = 7π/6, 3π/2, 11π/6.
Note: In Problems 10.28–10.29, you solve the equation 9 cos2x – 9 cos x + 2 = 0 using two different techniques. In each problem, identify the solutions on the interval 0 ≤ x < π.
10.28 Apply the quadratic formula to solve the equation.
The problem asks for the solutions that belong to the restricted range of arccosine 
. Neither 1/3 nor 2/3 are cosine values on the unit circle, so leave your answers in terms of arccosine.
Substitute a = 9, b = –9, and c = 2 into the quadratic formula, and set the fraction equal to cos x.
Thus, the solutions to the equation are x = arccos (1/3), x = arccos (2/3).
Note: In Problems 10.28–10.29, you solve the equation 9 cos2 x – 9 cos x + 2 = 0 using two different techniques. In each problem, identify the solutions on the interval 0 ≤ x ≤ π.
10.29 Verify your answer to Problem 10.28 by factoring the quadratic expression and applying the zero-product property.
Factor the quadratic expression and set each factor equal to 0.
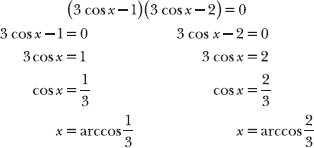
These solutions are identical to the solutions in Problem 10.28.
10.30 Apply the quadratic formula to identify the solutions to the equation 12 cos2 x + 7 cos x = 10 on the interval 0 ≤ x ≤ π.
In order to apply the quadratic formula, one side of the quadratic equation must equal 0; subtract 10 from both sides of the equation.
12 cos2 x + 7 cos x – 10 = 0
Substitute a = 12, b = 7, and c = –10 into the quadratic formula and set it equal to cos x.
The range of cosine is –1 ≤ cos x ≤ 1, so –5/4 is not a valid cosine value. Therefore, the only solution to this equation is x = arccos (2/3).
Apply the quadratic formula, setting a = 4, b = –1, and c = 2.
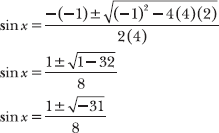
You cannot evaluate the square root of a negative number, so there are no real solutions to this trigonometric quadratic equation.
10.32 Identify the solutions to the equation 5 tan θ = –1 – 3 tan2θ on the interval –π/2 ≤ θ ≤ π/2.
Add 3 tan2θ and 1 to both sides of the equation.
3 tan2θ + 5 tan θ + 1 = 0
Substitute a = 3, b = 5, and c = 1 into the quadratic formula.
Arctangent is defined for all real numbers, so both of these solutions are valid.