Area of a Sector
Surface area of a pizza slice
12.35 Identify the formula used to calculate the area of a sector with central angle θ.
A sector is a portion of a circle bounded by an arc and two radii of the circle. To compute the area of a sector, you need to know the measure of its central angle θ and the radius r of the circle.
The vertex of a central angle lies on the center of a circle and its sides extend outward from the center, intersecting the circle.
Essentially, this formula multiplies the area of the full circle 
by a fraction that identifies how much of the circle is contained within the sector. For instance, a semicircle has a central angle of 180°, and its area is 180°/360° = 1/2 of the circle.
Note: Problems 12.36–12.39 refer to the diagram below, in which circle X has radius r = 2.
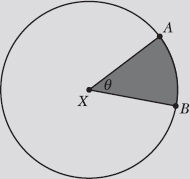
12.36 Calculate the area of circle X.
The area of a circle is the product of π and the squared radius (r2) of the circle. The problem states that the radius is r = 2.
Note: Problems 12.36–12.39 refer to the diagram in Problem 12.36. Note that circle X has radius r = 2.
12.37 Calculate the perimeter of the shaded sector, assuming θ is measured in radians.
The sector is bounded by two radii 
and an arc 
. Each of the radii has length 2. Apply the formula below to calculate the length of the arc.
The perimeter p of the sector is the sum of the lengths of the bounding radii and the arc.
If the central angle of an arc is measured in degrees rather than radians, the following formula calculates the length of that arc; the formula multiplies angle θ (measured in degrees) by π/180, thereby converting the angle measurement to radians.
Note: Problems 12.36–12.39 refer to the diagram in Problem 12.36. Note that circle X has radius r = 2.
12.38 Calculate the area of the shaded sector, assuming θ = π/6.
Apply the sector area formula presented in Problem 12.35. Note that the measure of the central angle is expressed in radians, so you should also use radians to express the measure of one full rotation: 2π.
Note: Problems 12.36–12.39 refer to the diagram in Problem 12.36. Note that circle X has radius r = 2.
12.39 Calculate the unshaded region of the circle, assuming θ = 40°.
The unshaded region of the circle is also a sector. Its central angle measures 360° – 40° = 320°. Because the central angle is expressed in degrees, you should also express the measure of one full rotation in degrees when applying the area formula.
Note: Problems 12.40–12.42 refer to a circle with radius 6 and a sector of the circle that has a central angle measuring 100°.
12.40 Calculate the area and circumference of the circle.
The area A of a circle is equal to the product of π and the square of the radius.
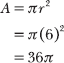
The circumference C of a circle is the product of 2π and the radius.
Note: Problems 12.40–12.42 refer to a circle with radius 6 and a sector of the circle that has a central angle measuring 100°.
12.41 Calculate the area of the sector.
Apply the area formula for the sector of a circle.
Note: Problems 12.40–12.42 refer to a circle with radius 6 and a sector of the circle that has a central angle measuring 100°.
12.42 Calculate the perimeter of the sector.
The perimeter of a sector consists of two radii and an arc of the circle. The radius of this circle is r = 6. To calculate the arc length, apply the formula introduced in Problem 12.37; use the version of the formula intended for central angles measured in degrees.
Add the lengths of the two radii to the arc length you calculated.
Note: Problems 12.43–12.45 refer to the diagram below, in which XY = 13 and XZ = 24.
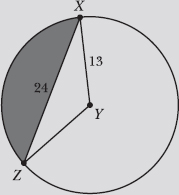
12.43 Calculate the area of the sector, bounded by 
Report the answer accurate to the thousandths place.
Two sides of triangle XYZ are also radii of circle Y, so they have the same length (XY = YZ = 13). Therefore, XYZ is an isosceles triangle. Draw 
, the segment connecting Y to the opposite side, and note that it is perpendicular to—and bisects—
.
See Problem 12.28.
By drawing the perpendicular bisector, you have divided XYZ into two congruent right triangles, WZY and WXY. Furthermore, you know that the measure of angle XYZ is equal to θ + θ. Apply a trigonometric ratio to calculate θ.
Therefore, the measure of central angle XYZ is equal to 2θ = 2arcsin (12/13). Apply the sector area formula. In the solution below, the calculator is set to degrees mode.
The area of the sector, accurate to the thousandths place, is 198.745.
Note: Problems 12.43–12.45 refer to the diagram in Problem 12.43, in which XY = 13 and XZ = 24.
12.44 Calculate the area of triangle XYZ.
As Problem 12.43 explains, XY = YZ = 13. You are given the length of the third side: XZ = 24. Calculate the semiperimeter of triangle XYZ.
Now apply Heron’s formula to calculate the area of triangle XYZ.
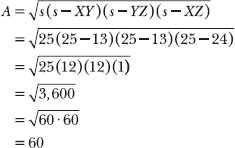
Note: Problems 12.43–12.45 refer to the diagram in Problem 12.43, in which XY = 13 and XZ = 24.
12.45 Calculate the area of the shaded region, accurate to the thousandths place.
The shaded region is the portion of the sector investigated in Problem 12.43 that does not include the area of triangle XYZ. Subtract the area you calculated in Problem 12.44 from the area you calculated in Problem 12.43.
