Given AAS, ASA, and occasionally SSA
13.1 Given the diagram below, in which A is opposite a, B is opposite b, and C is opposite c, state the law of sines.
The law of sines states that the ratio of the sine of an angle to the length of the opposite side is constant in a triangle.
You may also express the law of sines using the reciprocals of the ratios.
Note: Problems 13.2–13.4 refer to triangle ABC below.
13.2 Calculate b and report your answer accurate to the thousandths place.
You are given the measures of two angles and the length of a non-included side: 
and c = 4; in other words, you are given angle-angle-side (AAS). You are asked to calculate b, the side opposite angle B, which is also written AC. Because you know the measure of angle C and the length of the opposite side c, the ratio (sin C)/c should appear in the law of sines proportion. You are asked to calculate AC, which is equal to b, because it is the length of the side opposite angle B.
The side is not sandwiched between the two angles. In this diagram, 
is the side included between angles B and C.
AC and b are two different ways to write the same length. One names the side according to its endpoints and the other names the side according to the opposite angle.
Cross-multiply and solve for b.
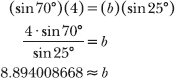
You conclude that b ≈ 8.894.
Note: Problems 13.2–13.4 refer to the diagram in Problem 13.2.
13.3 Calculate the measure of angle A.
The measures of the interior angles of a triangle have a sum of 180°. You are given two of those measures, so subtract them from 180° to calculate the measure of angle A.
Note: Problems 13.2–13.4 refer to the diagram in Problem 13.2.
13.4 Calculate the perimeter of ABC and report your answer accurate to three decimal places.
According to the diagram, the side opposite angle C has length c = 4; in Problem 13.2, you calculate b, the length of another side of the triangle. In order to compute the perimeter, you need to calculate the length of the remaining side, a. Apply the law of sines once again.
According to Problem 13.3, the measure of angle A is 85°. Note that you can replace (sin C)/c with (sin B)/b in the proportion above, now that you know the value of b. However, because b is a lengthy decimal and c is an integer, (sin C)/c is preferred.
Add the lengths of the sides to calculate the perimeter of ABC.
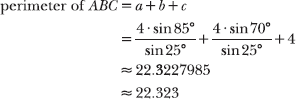
Substitute the exact values of a and b, the ugly fractions, into the formula. If you use decimals rounded to the thousandths place, it might lead to a rounding error, making your solution slightly inaccurate. If you hate typing fractions into your calculator, you can use the long decimal equivalents, but don’t round anything until the final step of the problem.
Problems 13.5–13.7 refer to triangle RST in the diagram below.
13.5 Calculate the measure of angle R.
The measures of two interior angles of triangle RST are given. Subtract them from 180° to calculate the measure of the remaining angle.
Problems 13.5–13.7 refer to triangle RST, illustrated in Problem 13.5.
13.6 Calculate RT, accurate to the thousandths place.
You are given the measure of two angles and the included side, or angle-side-angle (ASA). Apply the law of sines, noting that angle S is opposite side 
and angle R is opposite side 
According to Problem 13.5, the measure of angle R is 40°.
One fraction should always contain a known side length opposite a known angle measure (in this case, r and R). The other fraction should contain the side or angle you’re calculating and the side or angle opposite it (in this case, you are calculating s = RT and
Problems 13.5–13.7 refer to triangle RST, illustrated in Problem 13.5.
13.7 Calculate RS, accurate to the thousandths place.
Apply the law of sines, noting that t = RS because side 
is opposite angle T.
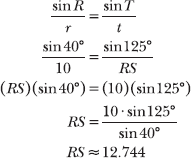
13.8 Calculate YZ in the triangle illustrated below. Report your answer accurate to the thousandths place.
You are given two angles and a non-included side (AAS), so apply the law of sines. Note that you are given the measure of angle Y (50°) and the length of the opposite side (y = 7). You are asked to calculate x = YZ, the length of the side opposite angle X.
Problems 13.9–13.12 refer to a triangle ABC, such that 
, a = 3, and c = 5.
13.9 Explain why the information provided by the problem classifies this as the ambiguous case for the law of sines.
You are given the measure of one angle and the lengths of two sides of triangle ABC. Note that one of the side lengths given (a = 3) is opposite the given angle measurement. Therefore, the angle is not formed by the sides, classifying this information as side-side-angle (SSA), rather than side-angle-side (SAS). Unlike the preceding problems in this chapter, you are given only one angle measurement, rather than two.
The angle included between two sides is the letter not named by the sides. In this case, angle B is included between (and formed by) sides a and c. If you had a triangle named MNP, and you were given side lengths n and p, those sides would form angle M, the remaining letter in the name of the triangle.
A SSA triangle is described as the ambiguous case, because the law of sines cannot always reliably predict whether or not an angle is obtuse when only one angle measurement is known. Because of this limitation, you should apply the law of cosines (described in Problems 13.13–13.24) to calculate any angle that may be obtuse, whenever possible. However, in this case, you must apply the law of sines and carefully interpret your answer.
Problems 13.9–13.12 refer to a triangle ABC, such that 
, a = 3, and c = 5.
13.10 Demonstrate, via an illustration drawn to scale, that angle C of triangle ABC may be acute or obtuse.
Use a ruler and a protractor to draw two different triangles named ABC with side lengths a = 3 and c = 5. Note that the angle opposite a must measure 20°. The diagram below illustrates two different triangles that meet these requirements; in one case, angle C is acute, and in the other, angle C is obtuse.
Because two different triangles may (and in this problem actually do) satisfy the SSA conditions described, there may be two different—and equally valid—ways to calculate the measures of the remaining sides and angles of the triangle. Hence, a SSA triangle is considered the ambiguous case for the law of sines. In Problems 13.11–13.12, you calculate the two possible measures of angle C.
Problems 13.9–13.12 refer to a triangle ABC, such that , a = 3, and c = 5.
13.11 Calculate the measure of angle C, assuming C is acute. Report your answer accurate to the thousandths place.
In the ambiguous case, you apply the law of sines and use arcsine to calculate the measure of an angle. Recall that the restricted range of arcsine is –π/2 ≤ θ ≤ π/2. Because triangles not on the coordinate plane must have positive angle measurements, arcsine will report an angle between 0 and π/2. In other words, unless the unknown angle is a right angle, it will be acute.
Therefore, 
.
Problems 13.9–13.12 refer to a triangle ABC, such that , a = 3, and c = 5.
13.12 Calculate the measure of angle C, assuming C is obtuse. Report your answer accurate to the thousandths place.
According to Problem 13.11, angle C has a sine value of approximately 0.5700335722. This is true whether C is acute or obtuse. An angle in standard position with a measure of approximately 34.753° has that sine value, and so does a reference angle with the same measure in the second quadrant. The terminal sides of both angles intersect the unit circle at the same height, so they have the same sine value, as illustrated below.
Angle C is the highlighted angle in the diagram, an obtuse angle in standard position that terminates in the second quadrant. Calculate its measure by subtracting the measure of its reference angle from 180° (as explained in Problem 4.7).
If C is an obtuse angle in triangle ABC, then it measures 145.247°.