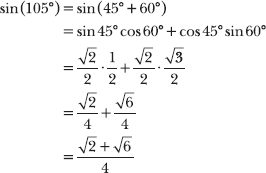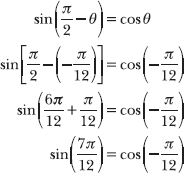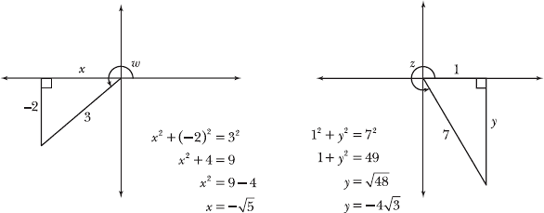Sum and Difference Formulas for Sine and Cosine
Expanding things like sin (x + y)
7.34 Apply an identity to express both of the following expressions as a sum of two products: sin (x + y) and sin (x – y).
Sum and difference identities allow you to rewrite a trigonometric statement whose argument is a sum or a difference. The result is usually not simpler; you transform a single trigonometric statement into a sum or difference of two products. Though these identities do not necessarily simplify an expression, they are no less important.
The argument of sin (x + y) is (x + y).
sin (x + y) = sin x cos y + cos x sin y sin(x – y) = sin x cos y – cos x sin y
Notice that the left-hand formula above contains addition signs on both sides of the equation. In the right-hand formula, both are replaced by subtraction signs. Because the signs match, some textbooks combine the pair of formulas into a single formula, as demonstrated below.
If the argument has addition in it, you substitute an expression that also contains addition. Subtraction works the same way.
sin (x ± y) = sin x cos y ± cos x sin y
Note: Problems 7.35–7.36 demonstrate two different ways to calculate sin 105°, an angle not on the standard unit circle, using two angles that do appear on the standard unit circle.
7.35 Given 45° + 60° = 105°, apply a sum formula to calculate the exact value of sin 105°.
Because 45° + 60° = 105°, you can write the expression sin 105° as sin (45° + 60°). Notice that both of the angles in the sum appear in the unit circle (45° = π/4 radians and 60° = π/3 radians), and you should have these sine and cosine values committed to memory. Apply the sum formula for sine (stated in Problem 7.34).
Note: Problems 7.35–7.36 demonstrate two different ways to calculate sin 105°, an angle not on the standard unit circle, using two angles that do appear on the standard unit circle.
7.36 Given 135° – 30° = 105°, apply a difference formula to calculate sin 105°.
In Problem 7.35, you apply a sum formula to calculate sin 105°. In this problem, you apply a difference formula, and the results are equal. Note that 135° = 3π/4 radians and 30° = π/6 radians.
7.37 Apply an identity to rewrite each of the following expressions as a sum of two products: cos (x + y) and cos (x – y).
The cosine sum and difference formulas are similar to the sine sum and difference formulas, with two major dissimilarities. Rather than products of different trigonometric functions (like sin x cos y), the cosine formulas contain products of the same function (cos x cos y). Furthermore, the signs within the formulas are opposites; if the argument contains an addition sign, you expand it into an expression containing a subtraction sign.
cos (x + y) = cos x cos y – sin x sin y cos (x – y) = cos x cos y + sin x sin y
Because the two signs in each expression are opposites, some textbooks combine the formulas above into a single formula using the symbols “
” to indicate the change in sign.
Note: Problems 7.38–7.39 explain how to calculate cos 
, an angle not on the standard unit circle, using two angles that do appear on the standard unit circle.
7.38 Identify two angles on the unit circle that have a difference of 
.
Notice that 
, as demonstrated below.
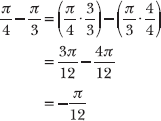
Note: Problems 7.38–7.39 explain how to calculate cos 
, an angle not on the standard unit circle, using two angles that do appear on the standard unit circle.
7.39 Apply the difference formula for cosine to the angles you identified in Problem 7.38 to calculate cos 
.
Recall that cos (x – y) = cos x cos y + sin x sin y.
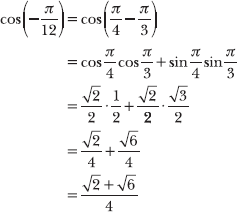
7.40 Compare the trigonometric values calculated in Problems 7.35, 7.36, and 7.39, and justify the similarities or differences.
According to Problems 7.35, 7.36, and 7.39, sin 105° = cos (–π/12). To explain why this is true, it is helpful to express the degree measure in radians.
Therefore, these problems conclude that sin (7π/12) = cos (–π/12). This is true according to the cofunction identity sin (π/2 – θ) = cos θ, if θ = –π/12.
While it may be, at first, surprising that sin 105° = cos (–π/12), a cofunction identity easily verifies the equality of the statements.
7.41 Verify the cofunction identity 
.
Apply the difference formula for cosine to expand the left side of the equation and demonstrate that both sides of the statement are equal.
7.42 Students often mistakenly apply the distributive property to trigonometric arguments, resulting in incorrect claims such as 
. Demonstrate that this statement is incorrect.
Do you see the error here? You can’t distribute the letters “sin” through parentheses. Those letters don’t represent a value—they are just the name of the function.
Evaluate each side of the equation individually and then compare the values to demonstrate they are unequal. Begin with the left side of the equation.
Now simplify the right side of the original statement.
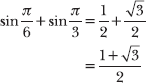
The left and right sides of the original statement have different values, so the original statement is incorrect.
.Apply the difference formulas for sine and cosine.
7.44 Verify the statement: sin (x + y) + sin (x – y) = 2 sin x cos y.
Expand the expressions on the left side of the equation and simplify.
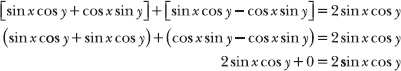
The two sides of the equation are clearly equal, so the original statement is verified.
7.45 Given an angle w that terminates in the third quadrant and an angle z that terminates in the fourth quadrant, such that 
, calculate sin (w + z).
Two angles, w and z, are described in this problem. You are given the quadrant in which those angles terminate, and you are provided one trigonometric value of each angle. In order to solve the problem, however, you will need additional information, as you discover when you expand the expression sin (w + z).
sin (w + z) = sin w cos z + cos w sin z
While you are given the values of sin w and cos z, you also need the values of cos w and sin z to substitute into the sum formula for sine. Apply the techniques described in Problems 4.36–4.43 (and illustrated in the following diagram), to calculate the missing values.
x and y have negative SIGNED values because x is left of, and y is below, the origin.
According to the diagram, 
. Substitute these values, and the original values given by the problem, into the expanded sum formula for sine.
