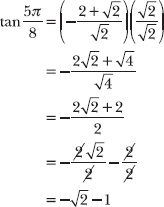Sum/difference, double/half-angle, and power-reducing formulas
8.36 Apply a sum or difference formula to calculate tan 75° without using a calculator or trigonometric table.
Problems 7.34–7.45 explore the sum and difference formulas for sine and cosine; the sum/difference formula for tangent is presented below.
![]()
In other words, tan (x + y) ![]() and tan (x – y)
and tan (x – y) ![]()
Note that “±” symbols appear on the left side of the equation and in the numerator of the fraction. Therefore, those signs match. The symbol “![]() ” represents the opposite sign.
” represents the opposite sign.
Notice that 75° = 30° + 45°. Therefore, you can calculate tan 75° by substituting x = 30° and y = 45° (or x = 45° and y = 30°) into the sum formula for tangent.
![]()
In order to evaluate this expression, you must calculate tan 30° and tan 45°.

Substitute these values into the expression and simplify.

Multiply the numerator and denominator by 3 to simplify the complex fraction.
![]()
Apply the tangent difference formula, stated in Problem 8.36.
![]()
Note that ![]()

8.38 Simplify the expression: ![]() .
.
Begin by expressing the fraction as the numerator multiplied by the reciprocal of the denominator. Next, apply the sum formula for tangent and the difference formula for sine.


Rewrite tan θ as the quotient of sin θ and cos θ to simplify the product.
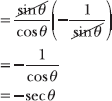
8.39 Generate the tangent double-angle formula based on the sum formula for tangent.
Express tan 2x as tan (x + x) and apply the sum formula introduced in Problem 8.36.

Substitute x = π/6 into the double-angle formula generated in Problem 8.39 and verify that the resulting statement is true.
![]()
Note that ![]() .
.
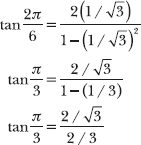
Express tan (π/3) in terms of sine and cosine; then cross-multiply.

Cross-multiply once again.

Because the resulting statement is obviously true, you have verified that the tangent double-angle formula tan 2x is true when x = π/6.
8.41 Simplify the expression: ![]() .
.
Factor the denominator, which is a difference of perfect squares, and express the numerator in terms of sine and cosine.

Manipulate the numerator, rewriting the expressions in terms of tangent and secant. In addition, note that (1 + tan2 x) in the denominator is equal to sec2 x, according to a Pythagorean identity.
See Problem 7.23, which states 1 + tan2 x = sec2x.
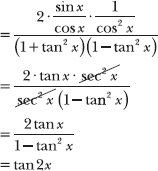
This is the tangent double-angle formula.
You conclude that ![]() .
.
8.42 Generate the power-reducing formula for tan2 θ by applying the power-reducing formulas for sin2 θ and cos2θ.
Note that tan2 θ = (sin2 θ)/(cos2 θ) and apply the power-reducing formulas from Problem 8.17.
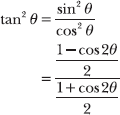
Multiply the numerator and denominator by 2 in order to simplify the complex fraction.

8.43 Apply a power-reducing formula to calculate the exact value of ![]() without using a calculator or trigonometric table.
without using a calculator or trigonometric table.
Applying the power-reducing formula for tangent produces double-angle trigonometric expressions. Note that 2(π/12) = 2π/12 = π/6.

Square the expressions in the numerator and denominator individually.

Express the numerator and denominator in terms of a least common denominator.

Multiply this fraction by 4/4 to cancel out the denominators.

8.44 Apply a half-angle formula to calculate the exact value of ![]() without using a calculator or trigonometric table.
without using a calculator or trigonometric table.
Unlike the sine and cosine half-angle formulas from Problems 8.22–8.23, there are two equivalent versions of the tangent half-angle formula. The formulas do not appear within a square root symbol, so they are not preceded by “±”.
You had to use quadrant clues to figure out the signs for cos (x/2) and sin (x/2). Not true for tan (x/2). The sign works itself out automatically.
![]()
Note that ![]() , so substitute θ = 5π/4 into one of the half-angle formulas above. Both produce the same final answer, but the right-hand formula requires less steps than the left in the context of this problem.
, so substitute θ = 5π/4 into one of the half-angle formulas above. Both produce the same final answer, but the right-hand formula requires less steps than the left in the context of this problem.

Rationalize the denominator to simplify the expression.
8.45 Demonstrate that the half-angle formula ![]() is true by evaluating it for θ = 2x.
is true by evaluating it for θ = 2x.
Substitute θ = 2x into the given half-angle formula and apply the following double-angle formulas: sin 2x = 2 sin x cos x and cos 2x = 2 cos2x – 1.
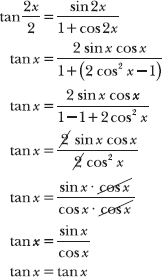
The final statement (tan x = tan x) is true, so you have verified that the original statement is true when θ = 2x.