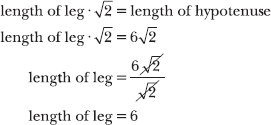Identifying Components Given Magnitude and Direction
Instead of coordinates
Note: Problems 15.37–15.38 refer to v = <x,y> with direction angle θ, as illustrated in the diagram below.
15.37 Evaluate cos θ, sin θ, and tan θ.
The length of the side adjacent to θ is x, the length of the side opposite θ is y, and the length of the hypotenuse is 
. Use these values to calculate cos θ, sin θ, and tan θ.
Note: Problems 15.37–15.38 refer to v = <x,y> with direction angle θ, as illustrated in Problem 15.37.
15.38 Identify the component form of v in terms of 
.
Note that the component form of the vector is v = <x,y>. According to Problem 15.37, cos θ = x/ 
and sin θ = y/
. Cross-multiply to solve these trigonometric equations for x and y.
Substitute these values into v = <x,y>.
This is the formula that calculates the component form of a vector v with direction angle θ and magnitude 
.
Note: Problems 15.39–15.40 refer to v = <x,y> with direction angle θ, as illustrated in the diagram below.
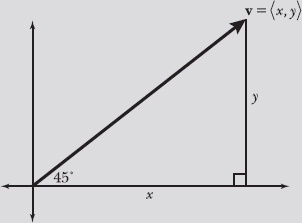
15.39 Given 
and θ = 45°, apply the vector component formula you generated in Problem 15.38 to express v in component form.
Substitute the magnitude and the direction angle into the formula 
. Note that 45° = π/4 radians, and cos 45° = sin 45° = 
You conclude that v = <6,6>.
Note: Problems 15.39–15.40 refer to v = <x,y> with direction angle θ, as illustrated in Problem 15.39.
15.40 Verify your answer to Problem 15.39 by applying the properties of a 45°–45°–90° triangle to calculate x and y.
The right triangle in the figure has angles that measure 45°, 45°, and 90°. Therefore, the length of the hypotenuse is equal to 
times the length of the legs. In this triangle, the hypotenuse has length 
and the legs have lengths x and y.
You know two angle measurements of the triangle: a right angle and a 45° angle at the origin. All three angles have to add up to 180°, so the third angle measures 45°.
Recall that the lengths of the legs of a 45°–45°–90° triangle are equal, so x = y = 6. These are also the components of the vector: v = <x,y> = <6,6>. This verifies your solution to Problem 15.39.
15.41 Given a vector w with direction angle θ = 180° and magnitude 
, express w in component form.
Substitute the angle and magnitude into the vector component formula generated in Problem 15.38. Note that 180° = π radians; thus, cos 180° = –1 and sin 180° = 0.
15.42 Given a vector r with direction angle θ = 135° and magnitude 
, express r in component form.
Note that 135° = 3π/4 radians, so cos 135° = 
and sin 135° = 
. Substitute these values, as well as the magnitude of r, into the vector component formula.
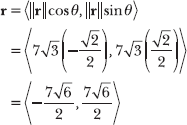
, express s in component form.Note that 60° = π/3 radians, so cos 60° = 1/2 and sin 60° = 
. Substitute these values into the vector component formula.
Note: In Problems 15.44–15.45, v has direction angle 30°, w has direction angle 270°, 
.
15.44 Express v and w in component form.
Apply the technique demonstrated in Problems 15.41–15.43 to express both vectors in component form. Note that 30° = π/6 radians and 270° = 3π/2 radians; both angles appear on the standard unit circle.
Note: In Problems 15.44–15.45, v has direction angle 30°, w has direction angle 270°, 
.
15.45 Determine whether the following statement is true and explain your answer.
This question asks whether the length of a vector sum is equal to the sum of the lengths of the individual vectors. In Problem 15.44, you express both vectors in component form. Begin this problem by calculating the sum v + w.
Calculate the magnitude of v + w.
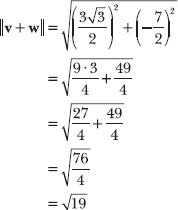
Notice that the magnitude of the sum is not equal to the sum of the individual magnitudes.
The magnitude of a vector sum is equal to the sum of the magnitudes of the individual vectors only when those vectors have the same direction angle. Vectors v and w do not have the same direction.