III.36 The Heat Equation

Igor Rodnianski

The heat equation was first proposed by FOURIER [VI.25] as a mathematical description of the transfer of heat in solid bodies. Its influence has subsequently been felt in many corners of mathematics: it provides explanations for such disparate phenomena as the formation of ice (the Stefan problem), the theory of incompressible viscous fluids (the NAVIERSTOKES EQUATION [III.23]), geometric flows (e.g., curve shortening, and the harmonic-map heat flow problem), BROWNIAN MOTION [IV.24], liquid filtration in porous media (the Hele-Shaw problem), index theorems (e.g., the Gauss-Bonnet-Chern formula), the price of stock options (the BLACK-SCHOLES FORMULA [VII.9 §2]), and the topology of three-dimensional manifolds (THE POINCARÉ CONJECTURE [V.25]). But the bright future Of the heat equation could have been predicted at its birth: after all, another small event that accompanied it was the creation of FOURIER ANALYSIS [III.27].

The propagation of heat is based on a simple continuity principle. The change in the quantity of heat u in a small volume ΔV over a small interval of time Δt is approximately

where C is the heat capacity of the substance and D is its density; but it is also given by the amount of heat entering and exiting through ΔV, which is approximately

where K is the heat conductivity constant and n is the unit normal to the boundary of ΔV.

Thus, setting the values of all physical constants to 1, dividing through by Δt and ΔV, and letting them tend to zero, we find that the evolution of the amount of heat (that is, the temperature) in a three-dimensional solid Ω is governed by the following classical heat equation, where u(t, x) is the temperature at time t at the point x = (x,y,z):

Here

is the three-dimensional Laplacian; Δu is the limit as the diameter of ΔV tends to zero of the quantity

To determine u(t,x), equation (1) needs to be complemented by the initial distribution u₀(x) = u(0,x) and boundary conditions on the solid interface ∂Ω. For example, for a solid unit cube C with surface maintained at zero temperature, the heat equation is considered as a problem with Dirichlet boundary conditions and, as was proposed by Fourier, u(t, x) can be found by the method of separation of variables by expanding u₀(x) into its Fourier series

which leads to the solution

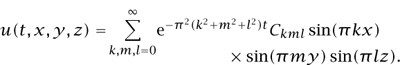
This simple example already illuminates a fundamental property of the heat equation: the tendency of its solutions to converge to an equilibrium state. In this case it reflects a physically intuitive fact that the temperature u (t, x) converges to the constant distribution u*(x) = C_000.

Propagation of heat in an insulated body corresponds to the choice of the Neumann boundary conditions, in which the normal derivative of u (normal, that is, to the boundary ∂Ω) is set to vanish. Its solutions can be constructed in a similar fashion.

The reason that Fourier analysis is intimately connected with the heat equation is that the trigonometric functions are EIGENFUNCTIONS [I.3 §4.3] of the Laplacian. A variety of more general heat equations can be obtained if one replaces the Laplacian by a more general linear, SELF-ADJOINT [III.50§ 3.2], nonnegative HAMILTONIAN [III.35] H with a discrete set of eigenvalues _n and corresponding eigenfunctions ψ_n. That is, one considers the heat flow

The solution u(t) is given by the formula u (t) = e-^tHu₀, where e^-tH is the heat semigroup generated by H, which also takes the more explicit form

Here the coefficients C_n are the Fourier coefficients of u₀ relative to H: that is, they are the coefficients that arise when we write u₀ as a sum (The existence of such a decomposition follows from the SPECTRAL THEOREM [III.50 §3.4] for self-adjoint operators. In a similar way, heat flows can also be generated by self- adjoint operators with a continuous spectrum.) In particular, the asymptotic behavior of u (t, x) as t → +∞ is completely determined by the spectrum of H.

Although explicit, representations like this do not provide very good quantitative descriptions of the behavior of the heat equation. To obtain such descriptions one has to abandon the idea of constructing solutions explicitly and look instead for principles and methods that apply to general classes of solutions while also being sufficiently robust to be useful in the analysis of more complicated heat equations.

The first methods of this type are called energy identities. To derive an energy identity, one multiplies the heat equation by a certain quantity, which may depend on the given solution, and integrates by parts. The simplest two identities of this type are the conservation of total heat of an insulated body,

and the energy identity,

The second identity already captures a fundamental smoothing property of the heat equation: since all three integrands are nonnegative and the first and third integrals are finite, the average of the mean-square gradient of u is finite, even if the initial mean-square gradient is infinite, and it even decreases to zero with t. In fact, away from the boundary of Ω an arbitrary amount of smoothing takes place, and not just on average but at every time t > 0.

The second fundamental principle of the heat equation is the global maximum principle

which tells us the familiar fact that the hottest spot in the body, over all time, is either on its boundary or in the initial distribution.

Finally, the diffusive properties of the heat equation in ⁿ are captured by the Harnack inequality for nonnegative solutions u. It tells us that

when t₂ > t₁. This tells us that if the temperature at x_l at time t₁ takes a certain value, then the temperature at x₂ at time t₂ cannot be too much smaller.

This form of the Harnack inequality features a very important object in the study of the heat equation, called the heat kernel:

One of its many uses is that it allows one to construct solutions of the heat equation in the whole of space (that is, in ⁿ) from initial data u,₀ by the formula

It also shows that after a time t initial point disturbances become distributed in a ball of radius around the point of the original disturbance. This sort of relation between spatial scales and timescales is the characteristic parabolic scaling of the heat equation.

As was shown by Einstein, the heat equation is intimately connected with the diffusion process of Brownian motion. In fact, the mathematical description of Brownien motion is in terms of a random process B_t with transitional probability densities given by the heat kernel p (t,x,y). For the n-dimensional Brownian motion starting at x, the function

u(t, x = E[u₀ ()]

computed with the help of expectation value is precisely the solution of the heat equation in ⁿ with initial data u₀(x). This connection is the start of a mutually beneficial relationship between the theory of the heat equation and probability. Among the most profitable applications of this relationship is the Feynman-Kac formula

which connects Brownian motion with solutions of the heat equation

with initial data u₀(x).

The three fundamental principles of the heat equation described above are remarkably robust, in the sense that they, or weaker versions of them, hold even for very general variants of the classical equation. For instance, they can be applied to the question of the continuity of solutions of the heat equation

where all that is assumed of the coefficients a_ij is that they are bounded and that they satisfy the ellipticity condition. One can even look at the equations in “nondiuergence form”:

Here, the connection between the heat equation and the corresponding stochastic diffusion process turns out to be particularly helpful. This analysis has led to beautiful applications in the CALCULUS OF VARIATIONS [III.94] and in fully nonlinear problems.

The same principles also hold for the heat equations On RIEMANNIAN MANIFOLDS [I.3 §6.10]. The appropriate analogue of the Laplacien for a manifold M is the Laplace-Beltrami operator Δ_M, and the heat equation for M is

If the Riemannian metric is g, then in local coordinates Δ_M takes the form

In this case, a version of the Harnack inequality holds for the heat equation on a manifold that has RICCI CURVATURE [III.78] bounded from below. Interest in the heat equations on manifolds is in part motivated by nonlinear geometric flows and attempts to understand their long-term behavior. One of the earliest geometric flows was the harmonic map flow

which describes a deformation of the map Φ(t,·) between two compact Riemannian manifolds M and N. The operator is a nonlinear Laplacian that is constructed by projecting Δ_M onto the tangent space of N. This is a gradient flow associated with the energy

it measures the stretching of the map U between M and N. Under the assumption that the sectional curvature of N is nonpositive, it can be shown that the harmonic map heat flow is regular and converges, as t → + ∞, to a harmonic map between M and N, which is a critical point of the energy functional E[ U]. This heat equation is used to establish the existence of harmonic maps and to construct a continuous deformation of a given map Φ (0, ·) to a harmonic map Φ (+ ∞,·). The curvature assumption on the target manifold N is responsible for the crucial monotonicity properties of the harmonic map heat flow, which come to light through the use of the energy estimates.

An even more spectacular application of a deformation principle of this kind appears in the three- dimensional RICCI FLOW [III.78]

This is a quasilinear heat evolution of a family of metrics g_ij(t) on a given manifold M. In this case the flow is not necessarily regular; nonetheless, it can be extended as a flow with “surgeries” in such a way that the structure of the surgeries and the long-term behavior of the flow can be precisely analyzed. This analysis shows in particular that any three-dimensional simply connected manifold is diffeomorphic to a three-dimensional sphere, which gives the proof of the Poincaré conjecture.

The long-term behavior of the heat equation is also important in the analysis of reaction-diffusion systems and associated biological phenomena. This was suggested already in the work of TURING [VI.94] in his attempt to understand morphogenesis (the formation of inhomogeneous patterns such as animal coat patterns from a nearly homogeneous initial state) by means of exponential instabilities in the reaction-diffusion equations

These examples emphasize the long-term behavior of the heat equation, and in particular the tendency of its solutions to converge to an equilibrium, or alternatively to develop exponential instabilities. However, it turns out that the short-term behavior of the heat equation on a manifold M is of the utmost importance in connection with the geometry and topology of M. This connection is twofold: first, one seeks to establish a relationship between the spectrum of Δ_M and the geometry of M; second, one can use an analysis of the short-term behavior to prove index theorems. The former aspect, in the context of planar domains, is captured by Marc Kac’s well-known question, “Can one hear the shape of a drum?” For manifolds it begins with the Weyl formula

as t tends to 0. The left-hand side of the identity is the trace of the heat kernel of Δ_M. That is,

where p (t, x, y) is such that any solution of the heat equation ∂u/∂t - Δ_Mu = 0 with u(0, x) = u₀(x) is given by the expression

The right-hand side of the Weyl identity reflects the short-term asymptotics of the heat kernel p(t, x, y).

The heat-flow approach to the proof of the index theorems can be viewed as a refinement of both sides of the Weyl identity. The trace on the left-hand side is replaced by a more complicated “super-trace,” while the right-hand side involves full asymptotics of the heat kernel, which requires one to understand subtle cancelations. The simplest example of this kind is the Gauss-Bonnet formula

which connects the Euler characteristic of a two-dimensional manifold M and the integral of its scalar curvature. The Euler characteristic X(M) arises from a linear combination of traces of the heat flows associated with the Hodge Laplacian (d + d*)² restricted to the space of exterior differential 0-forms, 1-forms, and 2-forms. A proof of a general ATIYAH-SINGER INDEX THEOREM [V.2] involves heat flows associated with an operator given by the square of a Dirac operator.