IV.11 Harmonic Analysis
Terence Tao
1 Introduction
Much of analysis tends to revolve around the study of general classes of FUNCTIONS [I.2 §2.2] and OPERATORS [III.50]. The functions are often real-valued or complex- valued, but may take values in other sets, such as a VECTOR SPACE [I.3 §2.3] or a MANIFOLD [I.3 §6.9]. An operator is itself a function, but at a “second level,” because its domain and range are themselves spaces of functions: that is, an operator takes a function (or perhaps more than one function) as its input and returns a transformed function as its output. Harmonic analysis focuses in particular on the quantitative properties of such functions, and how these quantitative properties change when various operators are applied to them.1
What is a “quantitative property” of a function? Here are two important examples. First, a function is said to be uniformly bounded if there is some real number M such that |f (x)| ≤ M for every x. It can often be useful to know that two functions f and g are “uniformly close,” which means that their difference f – g is uniformly bounded with a small bound M. Second, a function is called square integrable if the integral ∫|(x)|2 dx is finite. The square integrable functions are important because they can be analyzed using the theory of HILBERT SPACES [III.37].
A typical question in harmonic analysis might then be the following: if a function f : ![]() n →
n → ![]() is square integrable, its gradient ∇f exists, and all the n components of f are also square integrable, does this imply that f is uniformly bounded? (The answer is yes when n = 1, and no, but only just, when n = 2; this is a special case of the Sobolev embedding theorem, which is of fundamental importance in the analysis of PARTIAL DIFFERENTIAL EQUATIONS [IV.12].) If so, what are theprecise bounds one can obtain? That is, given the integrals of | f |2 and |∇f)i|2, what can you say about theuniform bound M that you obtain for f?
is square integrable, its gradient ∇f exists, and all the n components of f are also square integrable, does this imply that f is uniformly bounded? (The answer is yes when n = 1, and no, but only just, when n = 2; this is a special case of the Sobolev embedding theorem, which is of fundamental importance in the analysis of PARTIAL DIFFERENTIAL EQUATIONS [IV.12].) If so, what are theprecise bounds one can obtain? That is, given the integrals of | f |2 and |∇f)i|2, what can you say about theuniform bound M that you obtain for f?
Real and complex functions are of course very familiar in mathematics, and one meets them in high school. In many cases one deals primarily with SPECIAL FUNCTIONS [III.85]: polynomials, exponentials, trigonometric functions, and other very concrete and explicitly defined functions. Such functions typically have a very rich algebraic and geometric structure, and many questions about them can be answered exactly using techniques from algebra and geometry.
However, in many mathematical contexts one has to deal with functions that are not given by an explicit formula. For example, the solutions to ordinary and partial differential equations often cannot be given in an explicit algebraic form (as a composition of familiar functions such as polynomials, EXPONENTIAL FUNCTIONS [III.25], and TRIGONOMETRIC FUNCTIONS [III.92]). In such cases, how does one think about a function? The answer is to focus on its properties and see what can be deduced from them: even if the solution of a differential equation cannot be described by a useful formula, one may well be able to establish certain basic facts about it and be able to derive interesting consequences from those facts. Some examples of properties that one might look at are measurability, boundedness, continuity, differentiability, smoothness, analyticity, integrability, or quick decay at infinity One is thus led to consider interesting general classes of functions: to form such a class one chooses a property and takes the set of all functions with that property. Generally speaking, analysis is much more concerned with these general classes of functions than with individual functions. (See also FUNCTION SPACES [III.29].)
This approach can in fact be useful even when one is analyzing a single function that is very structured and has an explicit formula. It is not always easy, or even possible, to exploit this structure and formula in a purely algebraic manner, and then one must rely (at least in part) on more analytical tools instead. A typical example is the Airy function
![]()
Although this is defined explicitly as a certain integral, if one wants to answer such basic questions as whether Ai(x) is always a convergent integral, and whether this integral goes to zero as x → ± ο∞, it is easiest to proceed using the tools of harmonic analysis. In this case, one can use a technique known as the principle of stcitionciry phase to answer both these questions affirmatively, although there is the rather surprising fact that the Airy function decays almost exponentially fast as x → ±+∞, but only polynomially fast as x → – ∞.
Harmonic analysis, as a subfield of analysis, is particularly concerned not just with qualitative properties like the ones mentioned earlier, but also with quantitative bounds that relate to those properties. For instance, instead of merely knowing that a function f is bounded, one may wish to know how bounded it is. That is, what is the smallest M ≥ 0 such that |f(x) ≤ M for all (or almost all) x ∈ ![]() ; this number is known as the sup norm or L∞ -norm of f, and is denoted ||f||L∞. Or instead of assuming that f is square integrable one can quantify this by introducing the L2 -norm ||f||L2 = (∫ |f (x)|2 dx)½; more generally one can quantify pth-power integrability for 0 < p < ∞ via the Lp-norm ||f|| Lp = (∫ |f (x) |p dx)1/p. Similarly, most of the other qualitative properties mentioned above can be quantified by a variety of NORMS [III.62], which assign a nonnegative number (or +∞) to any given function and which provide some quantitative measure of one characteristic of that function. Besides being of importance in pure harmonic analysis, quantitative estimates involving these norms are also useful in applied mathematics, for instance in performing an error analysis of some numerical algorithm.
; this number is known as the sup norm or L∞ -norm of f, and is denoted ||f||L∞. Or instead of assuming that f is square integrable one can quantify this by introducing the L2 -norm ||f||L2 = (∫ |f (x)|2 dx)½; more generally one can quantify pth-power integrability for 0 < p < ∞ via the Lp-norm ||f|| Lp = (∫ |f (x) |p dx)1/p. Similarly, most of the other qualitative properties mentioned above can be quantified by a variety of NORMS [III.62], which assign a nonnegative number (or +∞) to any given function and which provide some quantitative measure of one characteristic of that function. Besides being of importance in pure harmonic analysis, quantitative estimates involving these norms are also useful in applied mathematics, for instance in performing an error analysis of some numerical algorithm.
Functions tend to have infinitely many degrees of freedom, and it is thus unsurprising that the number of norms one can place on a function is infinite as well: there are many ways of quantifying how “large” a function is. These norms can often differ quite dramatically from each other. For instance, if a function f is very large for just a few values, so that its graph has tall, thin “spikes,” then it will have a very large L∞-norm, but ∫|f (x) | dx, its L1-norm, may well be quite small. Conversely, if f has a very broad and spread-out graph, then it is possible for ∫ |f(x) | dx to be very large even if |f(x| is small for every x: such a function has a large L1-norm but a small L∞-norm. Similar examples can be constructed to show that the L2-norm sometimes behaves very differently from either the L1-norm or the L°°-norm. However, it turns out that the L2-norm lies “between” these two norms, in the sense that if one controls both the L1-norm and the L1-norm, then one also automatically controls the L2-norm. Intuitively, the reason is that if the L∞-norm is not too large then one eliminates all the spiky functions, and if the L1 -norm is small then one eliminates most of the broad functions; the remaining functions end up being well-behaved in the intermediate L2-norm. More quantitatively, we have the inequality
![]()
which follows easily from the trivial algebraic fact that if if |f(x) ≤, M then |f (x)|2 ≤ M|f (x) |. This inequality is a special case Of HÖLDER’S INEQUALITY [V.19], which is one of the fundamental inequalities in harmonic analysis. The idea that control of two “extreme” norms automatically implies further control on “intermediate” norms can be generalized tremendously and leads to very powerful and convenient methods known as interpolation, which is another basic tool in this area.
The study of a single function and all its norms eventually gets somewhat tiresome, though. Nearly all fields of mathematics become a lot more interesting when one considers not just objects, but also maps between objects. In our case, the objects in question are functions, and, as was mentioned in the introduction, a map that takes functions to functions is usually referred to as an operator.(In some contexts it is also called a TRANSFORM [III.91].) Operators may seem like fairly complicated mathematical objects—their inputs and outputs are functions, which in turn have inputs and outputs that are usually numbers—but they are in fact a very natural concept since there are many situations where one wants to transform functions. For example, differentiation can be thought of as an operator, which takes a function f to its derivative df/dx. This operator has a well-known (partial) inverse, integration, which takes f to the function F that is defined by the formula
![]()
A less intuitive, but particularly important, example is THE FOURIER TRANSFORM [III.27]. This takes f to a function ![]() , given by the formula
, given by the formula
![]()
It is also of interest to consider operators that take two or more inputs. Two particularly common examples are the pointwise product and convolution. If f and g are two functions, then their pointwise product fg is defined in the obvious way:
(fg)(x) f(x)g(x).
The convolution, denoted f * g, is defined as follows:
![]()
This is just a very small sample of interesting operators that one might look at. The original purpose of harmonic analysis was to understand the operators that were connected to Fourier analysis, real analysis, and complex analysis. Nowadays, however, the subject has grown considerably, and the methods of harmonic analysis have been brought to bear on a much broader set of operators. For example, they have been particularly fruitful in understanding the solutions of various linear and nonlinear partial differential equations, since the solution of any such equation can be viewed as an operator applied to the initial conditions. They are also very useful in analytic and combinatorial number theory, when one is faced with understanding the oscillation present in various expressions such as exponential sums. Harmonic analysis has also been applied to analyze operators that arise in geometric measure theory, probability theory, ergodic theory, numerical analysis, and differential geometry.
A primary concern of harmonic analysis is to obtain both qualitative and quantitative information about the effects of these operators on generic functions. A typical example of a quantitative estimate is the inequality
||f * g|| L∞ ≤ ||f|| L2 ||g|| L2,
which is true for all f,g ∈ L2. This result, which is a special case of Young’s inequality, is easy to prove: one just writes out the definition of f * g(x) and applies the CAUCHY-SCHWARZ INEQUALITY [V.19]. As a consequence, one can draw the qualitative conclusion that the convolution of two functions in L2 is always continuous. Let us briefly sketch the argument, since it is an instructive one.
A fundamental fact about functions in L2 is that any such function f can be approximated arbitrarily well (in the L2-norm) by a function ![]() that is continuous and compactly supported. (The second condition means that
that is continuous and compactly supported. (The second condition means that ![]() takes the value zero everywhere outside some interval [—M, M].) Given any two functions f and g in L2, let
takes the value zero everywhere outside some interval [—M, M].) Given any two functions f and g in L2, let ![]() and
and ![]() be approximations of this kind. It is an exercise in real analysis to prove that
be approximations of this kind. It is an exercise in real analysis to prove that ![]() *
* ![]() is continuous, and it follows easily from the inequality above that
is continuous, and it follows easily from the inequality above that ![]() *
* ![]() is close to f * g in the L∞-norm, since
is close to f * g in the L∞-norm, since
f * g - ![]() *
* ![]() = f * (g -
= f * (g - ![]() ) + (f -
) + (f - ![]() ) *
) * ![]() .
.
Therefore, f * g can be approximated arbitrarily well in the L∞-norm by continuous functions. A standard result in basic real analysis (that a uniform limit of continuous functions is continuous) now tells us that f * g is continuous.
Notice the general structure of this argument, which occurs frequently in harmonic analysis. First, one identifies a “simple” class of functions for which one can easily prove the result one wants. Next, one proves that every function in a much wider class can be approximated in a suitable sense by simple functions. Finally, one uses this information to deduce that the result holds for functions in the wider class as well. In our case, the simple functions were the continuous functions of finite support, the wider class consisted of square-integrable functions, and the suitable sense of approximation was closeness in the L2-norm.
We shall give some further examples of qualitative and quantitative analysis of operators in the next section.
2 Example: Fourier Summation
To illustrate the interplay between quantitative and qualitative results, we shall now sketch some of the basic theory of summation of Fourier series, which historically was one of the main motivations for studying harmonic analysis.
In this section, we shall consider functions f that are periodic with period 2π: that is, functions such that f(x + 2π) = f(x) for all x. An example of such a function is f(x) = 3 + sin(x) - 2 cos(3x). A function like this, which can be written as a finite linear combination of functions of the form sin(nx) and cos(nx), is called a trigonometric polynomial. The word “polynomial” is used here because any such function can be expressed as a polynomial in sin(x) and cos(x), or alternatively, and somewhat more conveniently, as a polynomial in eix and e-ix. That is, it can be written as ![]() for some N and some choice of coefficients (cn : -N ≤ n ≤ N). If we know that f can be expressed in this form, then we can work out the coefficient cn quite easily: it is given by the formula
for some N and some choice of coefficients (cn : -N ≤ n ≤ N). If we know that f can be expressed in this form, then we can work out the coefficient cn quite easily: it is given by the formula
![]()
It is a remarkable and very important fact that we can say something similar about a much wider class of functions—if, that is, we now allow infinite linear combinations. Suppose that f is a periodic function that is also continuous (or, more generally, that f is absolutely integrable, meaning that the integral of |f(x)| between 0 and 2π is finite). We can then define the Fourier coefficients ![]() (n) of f, using exactly the formula we had above for cn:
(n) of f, using exactly the formula we had above for cn:
![]()
The example of trigonometric polynomials now suggests that one should have the identity
![]()
expressing f as a sort of “infinite trigonometric polynomial,” but this is not always true, and even when it is true it takes some effort to justify it rigorously, or even to say precisely what the infinite sum means.
To make the question more precise, let us introduce for each natural number N the Dirichlet summation operator SN. This takes a function f to the function SNf that is defined by the formula

The question we would like to answer is whether SNf converges to f as N → ∞. The answer turns out to be surprisingly complicated: not only does it depend on the assumptions that one places on the function f, but it also depends critically on how one defines “convergence.” For example, if we assume that f is continuous and ask for the convergence to be uniform, then the answer is very definitely no: there are examples of continuous functions f for which SNf does not even converge pointwise to f. However, if we ask for a weaker form of convergence, the answer is yes: SNf will necessarily converge to f in the L![]() topology for any 0 <
topology for any 0 < ![]() < ∞, and even though it does not have to converge pointwise, it will converge almost everywhere, meaning that the set of x for which SNf(x) does not converge to x has MEASURE [III.55] zero. If instead one assumes only that f is absolutely integable, then it is possible for the partial sums SNf to diverge at every single point x, as well as being divergent in the L
< ∞, and even though it does not have to converge pointwise, it will converge almost everywhere, meaning that the set of x for which SNf(x) does not converge to x has MEASURE [III.55] zero. If instead one assumes only that f is absolutely integable, then it is possible for the partial sums SNf to diverge at every single point x, as well as being divergent in the L![]() topology for every
topology for every ![]() such that 0 <
such that 0 < ![]() ≤ ∞. The proofs of all of these results ultimately rely on very quantitative results in harmonic analysis, and in particular on various L
≤ ∞. The proofs of all of these results ultimately rely on very quantitative results in harmonic analysis, and in particular on various L![]() -type estimates on the Dirichlet sum SNf(x), as well as estimates connected with the closely related maximal operator, which takes f to the function supN>0 |SNf(x)|.
-type estimates on the Dirichlet sum SNf(x), as well as estimates connected with the closely related maximal operator, which takes f to the function supN>0 |SNf(x)|.
As these results are a little tricky to prove, let us first discuss a simpler result, in which the Dirichlet summation operators SN are replaced by the Fejér summation operators FN. For each N, the operator FN is the average of the first N Dirichlet operators: that is, it is given by the formula
![]()
It is not hard to show that if SNf converges to f, then so does FNf. However, by averaging the SNf we allow cancellations to take place that sometimes make it possible for FNf to converge to f even when SNf does not. Indeed, here is a sketch of a proof that FNf converges to f whenever f is continuous and periodic—which, as we have seen, is far from true of SNf.
In its basic structure, the argument is similar to the one we used when showing that the convolution of two functions in L2 is continuous. Note first that the result is easy to prove when f is a trigonometric polynomial, since then SNf = f for every N from some point onward. Now the Weierstrass approximation theorem says that every continuous periodic function f can be uniformly approximated by trigonometric polynomials: that is, for every ε > 0 there is a trigonometric polynomial such that ||f - g|| L∞ ≤ ε. We know that FNg is close to g for large N (since g is a trigonometric polynomial), and would like to deduce the same for f.
The first step is to use some routine trigonometric manipulation to prove the identity

The precise form of this expression is less important than two properties of the function
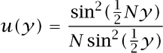
that we shall use. One is that u(y) is always nonnegative and the other is that ![]() These two facts allow us to say that
These two facts allow us to say that

That is, ||FNh|| L∞ ≤ ||h|| L∞ for any bounded function h.
To apply this result, we choose a trigonometric polynomial g such that ||f - g|| L∞ ≤ ε and let h = f - g. Then we find that ||FNh|| L∞ = ||FNf - FNg|| L∞ ≤ ε as well. As mentioned above, if we choose N large enough, then ||FNg - g|| L∞ ε, and then we use the TRIANGLE INEQUALITY [V.19] to say that
||FNf - f|| L∞ ≤ ||FNf - FNg|| L∞ + ||FNg - g|| L∞ + ||g - f|| L∞.
Since each term on the right-hand side is at most ε, this shows that ||FNf - f|| L∞ is at most 3ε. And since ε can be made arbitrarily small, this shows that FNf converges to f.
A similar argument (using MINKOWSKI’S INTEGRAL INEQUALITY [V.19] instead of the triangle inequality) shows that ||FNf|| L![]() ≤ ||f|| L
≤ ||f|| L![]() for all 1 ≤
for all 1 ≤ ![]() ≤ ∞, f ∈ L
≤ ∞, f ∈ L![]() , and N ≤ 1. As a consequence, one can modify the above argument to show that FNf converges to f in the L
, and N ≤ 1. As a consequence, one can modify the above argument to show that FNf converges to f in the L![]() topology for every f ∈ L
topology for every f ∈ L![]() . A slightly more difficult result (relying on a basic result in harmonic analysis known as the Hardy-Littlewood maximal inequality) asserts that, for every 1 <
. A slightly more difficult result (relying on a basic result in harmonic analysis known as the Hardy-Littlewood maximal inequality) asserts that, for every 1 < ![]() ≤ ∞, there exists a constant C
≤ ∞, there exists a constant C![]() such that one has the inequality ||supN |FNf| || L
such that one has the inequality ||supN |FNf| || L![]() ≤ C
≤ C![]() ||f|| L
||f|| L![]() for all f ∈ L
for all f ∈ L![]() ; as a consequence, one can show that FNf converges to f almost everywhere for every f ∈ L
; as a consequence, one can show that FNf converges to f almost everywhere for every f ∈ L![]() and 1 <
and 1 < ![]() ≤ ∞. A slight modification of this argument also allows one to treat the endpoint case when f is merely assumed to be absolutely integrable; see the discussion on the Hardy-Littlewood maximal inequality at the end of this article.
≤ ∞. A slight modification of this argument also allows one to treat the endpoint case when f is merely assumed to be absolutely integrable; see the discussion on the Hardy-Littlewood maximal inequality at the end of this article.
Now let us return briefly to Dirichlet summation. Using some fairly sophisticated techniques in harmonic analysis (such as Calderón-Zygmund theory) one can show that when 1 < ![]() < ∞ the Dirichlet operators SN are bounded in L
< ∞ the Dirichlet operators SN are bounded in L![]() uniformly in N. In other words, for every
uniformly in N. In other words, for every ![]() in this range there exists a positive real number C
in this range there exists a positive real number C![]() such that ||SNf|| L
such that ||SNf|| L![]() ≤ C
≤ C![]() ||f|| L
||f|| L![]() for every function f in L
for every function f in L![]() and every nonnegative integer N. As a consequence, one can show that SNf converges to f in the L
and every nonnegative integer N. As a consequence, one can show that SNf converges to f in the L![]() topology for all f in L
topology for all f in L![]() and every
and every ![]() such that 1 <
such that 1 < ![]() < ∞. However, the quantitative estimate on SN fails at the endpoints
< ∞. However, the quantitative estimate on SN fails at the endpoints ![]() = 1 and
= 1 and ![]() = ∞, and from this one can also show that the convergence result also fails at these endpoints (either by explicitly constructing a counterexample or by using general results such as the so-called uniform boundedness principle).
= ∞, and from this one can also show that the convergence result also fails at these endpoints (either by explicitly constructing a counterexample or by using general results such as the so-called uniform boundedness principle).
What happens if we ask for SNf to converge to f almost everywhere? Almost-everywhere convergence does not follow from convergence in L![]() when
when ![]() < ∞, so we cannot use the above results to prove it. It turns out to be a much harder question, and was a famous open problem, eventually answered by CARLESON’S THEOREM [V.5] and an extension of it by Hunt. Carleson proved that one has an estimate of the form ||supN |SNf| || L
< ∞, so we cannot use the above results to prove it. It turns out to be a much harder question, and was a famous open problem, eventually answered by CARLESON’S THEOREM [V.5] and an extension of it by Hunt. Carleson proved that one has an estimate of the form ||supN |SNf| || L![]() ≤ C
≤ C![]() ||f|| L
||f|| L![]() in the case
in the case ![]() = 2, and Hunt generalized the proof to cover all
= 2, and Hunt generalized the proof to cover all ![]() with 1 <
with 1 < ![]() < ∞. This result implies that the Dirichlet sums of an L
< ∞. This result implies that the Dirichlet sums of an L![]() function do indeed converge almost everywhere when 1 <
function do indeed converge almost everywhere when 1 < ![]() ∞. On the other hand, this estimate fails at the endpoint
∞. On the other hand, this estimate fails at the endpoint ![]() = 1, and there is in fact an example due to KOLNOGOROV [VI.88] of an absolutely integrable function whose Dirichlet sums are everywhere divergent. These results require a lot of harmonic analysis theory. In particular they use many decompositions of both the spatial variable and the frequency variable, keeping the Heisenberg uncertainty principle in mind. They then carefully reassemble the pieces, exploiting various manifestations of orthogonality.
= 1, and there is in fact an example due to KOLNOGOROV [VI.88] of an absolutely integrable function whose Dirichlet sums are everywhere divergent. These results require a lot of harmonic analysis theory. In particular they use many decompositions of both the spatial variable and the frequency variable, keeping the Heisenberg uncertainty principle in mind. They then carefully reassemble the pieces, exploiting various manifestations of orthogonality.
To summarize, quantitative estimates such as L![]() estimates on various operators provide an important route to establishing qualitative results, such as convergence of certain series or sequences. In fact there are a number of principles (notably the uniform boundedness principle and a result known as Stein’s maximal principle) which assert that in certain circumstances this is the only route, in the sense that a quantitative estimate must exist in order for the qualitative result to be true.
estimates on various operators provide an important route to establishing qualitative results, such as convergence of certain series or sequences. In fact there are a number of principles (notably the uniform boundedness principle and a result known as Stein’s maximal principle) which assert that in certain circumstances this is the only route, in the sense that a quantitative estimate must exist in order for the qualitative result to be true.
3 Some General Themes in Harmonic Analysis: Decomposition, Oscillation, and Geometry
One feature of harmonic analysis methods is that they tend to be local rather than global. For instance, if one is analyzing a function f it is quite common to decompose it as a sum f = f1 + · · · + fk, with each function fi “localized” in the sense that its support (the set of values x for which fi(x) ≠ 0) has a small diameter. This would be called localization in the spatial variable. One can also localize in the frequency variable by applying the process to the Fourier transform ![]() of f. Having split f up like this, one can carry out estimates for the pieces separately and then recombine them later. One reason for this “divide and conquer” strategy is that a typical function f tends to have many different features—for example, it may be very “spiky,” “discontinuous,” or “high frequency” in some places, and “smooth” or “low frequency” in others—and it is difficult to treat all of these features at once. A well-chosen decomposition of the function f can isolate these features from each other, so that each component has only one salient feature that could cause difficulty: the spiky part can go into one fi, the high-frequency part into another, and so on. In reassembling the estimates from the individual components, one can use crude tools such as the triangle inequality or more refined tools, for instance those relying on some sort of orthogonality, or perhaps a clever algorithm that groups the components into manageable clusters. The main drawback of the decomposition method (other than an aesthetic one) is that it tends to give bounds that are not quite optimal; however, in many cases one is content with an estimate that differs from the best possible one by a multiplicative constant.
of f. Having split f up like this, one can carry out estimates for the pieces separately and then recombine them later. One reason for this “divide and conquer” strategy is that a typical function f tends to have many different features—for example, it may be very “spiky,” “discontinuous,” or “high frequency” in some places, and “smooth” or “low frequency” in others—and it is difficult to treat all of these features at once. A well-chosen decomposition of the function f can isolate these features from each other, so that each component has only one salient feature that could cause difficulty: the spiky part can go into one fi, the high-frequency part into another, and so on. In reassembling the estimates from the individual components, one can use crude tools such as the triangle inequality or more refined tools, for instance those relying on some sort of orthogonality, or perhaps a clever algorithm that groups the components into manageable clusters. The main drawback of the decomposition method (other than an aesthetic one) is that it tends to give bounds that are not quite optimal; however, in many cases one is content with an estimate that differs from the best possible one by a multiplicative constant.
To give a simple example of the method of decomposition, let us consider the Fourier transform ![]() (ξ) of a function f:
(ξ) of a function f: ![]() →
→ ![]() , defined (for suitably nice functions f) by the formula
, defined (for suitably nice functions f) by the formula
![]()
What we can say about the size of ![]() , as measured by suitable norms, if we are given information about the size of f, as measured by other norms?
, as measured by suitable norms, if we are given information about the size of f, as measured by other norms?
Here are two simple observations in response to this question. First, since the modulus of e-2πixξ is always equal to 1, it follows that |![]() (ξ)| is at most ∫
(ξ)| is at most ∫![]() |f(x)| dx. This tells us that ||
|f(x)| dx. This tells us that ||![]() || L∞ ≤ || f||L1, at least if f - L1. In particular,
|| L∞ ≤ || f||L1, at least if f - L1. In particular, ![]() ∈ L∞. Secondly, the Plancherel theorem, a very basic fact of Fourier analysis, tells us that ||
∈ L∞. Secondly, the Plancherel theorem, a very basic fact of Fourier analysis, tells us that ||![]() || L2 is equal to ||f|| L2 if f ∈ L2. Therefore, if f belongs to L2 then so does
|| L2 is equal to ||f|| L2 if f ∈ L2. Therefore, if f belongs to L2 then so does ![]() .
.
We would now like to know what happens if f lies in an intermediate L![]() space. In other words, what happens if 1 <
space. In other words, what happens if 1 < ![]() < 2? Since L
< 2? Since L![]() is not contained in either L1 or L2, one cannot use either of the above two results directly. However, let us take a function f ∈ L
is not contained in either L1 or L2, one cannot use either of the above two results directly. However, let us take a function f ∈ L![]() and consider what the difficulty is. The reason f may not lie in L1 is that it may decay too slowly: for instance, the function f(x) = (1 + |x|)-¾ tends to zero more slowly than 1/x as x → ∞, so its integral is infinite. However, if we raise f to the power 3/2 we obtain the function (1 + |x|)-9/8 which decays quickly enough to have a finite integral, so f does belong to L3/2. Similar examples show that the reason f may fail to belong to L2 is that it can have places where it tends to infinity slowly enough for the integral of |f|
and consider what the difficulty is. The reason f may not lie in L1 is that it may decay too slowly: for instance, the function f(x) = (1 + |x|)-¾ tends to zero more slowly than 1/x as x → ∞, so its integral is infinite. However, if we raise f to the power 3/2 we obtain the function (1 + |x|)-9/8 which decays quickly enough to have a finite integral, so f does belong to L3/2. Similar examples show that the reason f may fail to belong to L2 is that it can have places where it tends to infinity slowly enough for the integral of |f|![]() to be finite but not slowly enough for the integral of |f|2 to be finite.
to be finite but not slowly enough for the integral of |f|2 to be finite.
Notice that these two reasons are completely different. Therefore, we can try to decompose f into two pieces, one consisting of the part where f is large and the other consisting of the part where f is small. That is, we can choose some threshold λ and define f1(x) to be f(x) when |f(x)| < λ and 0 otherwise, and define f2(x) to be f(x) when |f(x)| ≥ λ and 0 otherwise. Then f1 + f2 = f, and f1 and f2 are the “small part” and “large part” of f, respectively.
Because |f1(x)| < λ for every x, we find that
|f1(x)|2 = |f1(x)|2-![]() |f1(x)|
|f1(x)|![]() < λ2-
< λ2-![]() |f1(x)|
|f1(x)|![]() .
.
Therefore, f1 belongs to L2 and ||f1|| L2 ≤ λ2-![]() ||f1|| L
||f1|| L![]() . Similarly, because |f2(x)| ≥ λ whenever f2(x) ≠ 0, we have the inequality |f2(x) ≤ |f2(x)|
. Similarly, because |f2(x)| ≥ λ whenever f2(x) ≠ 0, we have the inequality |f2(x) ≤ |f2(x)|![]() / λ
/ λ![]() -1 for every x, which tells us that f2 belongs to L1 and that ||f2|| L1 ≤ ||f2|| L
-1 for every x, which tells us that f2 belongs to L1 and that ||f2|| L1 ≤ ||f2|| L![]() /λ
/λ![]() -1.
-1.
From our knowledge about the L2-norm of f1 and the L1-norm of f2 we can obtain upper bounds for the L2-norm of ![]() 1 and the L∞-norm of
1 and the L∞-norm of ![]() 2, by our remarks above. By using this strategy for every λ and combining the results in a clever way, one can obtain the Hausdorff-Young inequality, which is the following assertion. Let
2, by our remarks above. By using this strategy for every λ and combining the results in a clever way, one can obtain the Hausdorff-Young inequality, which is the following assertion. Let ![]() lie between 1 and 2 and let p' be the dual exponent of
lie between 1 and 2 and let p' be the dual exponent of ![]() , which is the number
, which is the number ![]() /(
/(![]() - 1). Then there is a constant C
- 1). Then there is a constant C![]() such that, for every function f ∈ L
such that, for every function f ∈ L![]() , one has the inequality ||
, one has the inequality ||![]() || L
|| L![]() ' ≤ C
' ≤ C![]() ||f|| L
||f|| L![]() . The particular decomposition method we have used to obtain this result is formally known as the method of real interpolation. It does not give the best possible value of C
. The particular decomposition method we have used to obtain this result is formally known as the method of real interpolation. It does not give the best possible value of C![]() , which turns out to be
, which turns out to be ![]() 1/2
1/2![]() /(
/(![]() ')1/2
')1/2![]() ', but that requires more delicate methods.
', but that requires more delicate methods.
Another basic theme in harmonic analysis is the attempt to quantify the elusive phenomenon of oscillation. Intuitively, if an expression oscillates wildly, then we expect its average value to be relatively small in magnitude, since the positive and negative parts, or in the complex case the parts with a wide range of different arguments, will cancel out. For instance, if a 2π-periodic function f is smooth, then for large n the Fourier coefficient
![]()
will be very small since ![]() and the comparatively slow variation in f(x) is not enough to stop the cancellation occurring. This assertion can easily be proved rigorously by repeated integration by parts. Generalizations of this phenomenon include the so-called principle of stationary phase, which among other things allows one to obtain precise control on the Airy function Ai(x) discussed earlier. It also yields the Heisenberg uncertainty principle, which relates the decay and smoothness of a function to the decay and smoothness of its Fourier transform.
and the comparatively slow variation in f(x) is not enough to stop the cancellation occurring. This assertion can easily be proved rigorously by repeated integration by parts. Generalizations of this phenomenon include the so-called principle of stationary phase, which among other things allows one to obtain precise control on the Airy function Ai(x) discussed earlier. It also yields the Heisenberg uncertainty principle, which relates the decay and smoothness of a function to the decay and smoothness of its Fourier transform.
A somewhat different manifestation of oscillation lies in the principle that if one has a sequence of functions that oscillate in different ways, then their sum should be significantly smaller than the bound that follows from the triangle inequality. Again, this is the result of cancellation that is simply not noticed by the triangle inequality. For instance, the Plancherel theorem in Fourier analysis implies, among other things, that a trigonometric polynomial ![]() has an L2-norm of
has an L2-norm of

This bound (which can also be proved by direct calculation) is smaller than the upper bound of ![]() that would be obtained if we simply applied the triangle inequality to the functions cneinx. This identity can be viewed as a special case of the Pythagorean theorem, together with the observation that the harmonics einx are all orthogonal to each other with respect to the INNER PRODUCT [III.37]
that would be obtained if we simply applied the triangle inequality to the functions cneinx. This identity can be viewed as a special case of the Pythagorean theorem, together with the observation that the harmonics einx are all orthogonal to each other with respect to the INNER PRODUCT [III.37]
![]()
This concept of orthogonality has been generalized in a number of ways. For instance, there is a more general and robust concept of “almost orthogonality,” which roughly speaking means that the inner products of a collection of functions are small but not necessarily 0.
Many arguments in harmonic analysis will, at some point, involve a combinatorial statement about certain types of geometric objects such as cubes, balls, or boxes. For instance, one useful such statement is the Vitali covering lemma, which asserts that, given any collection B1, . . . ,Bk of balls in Euclidean space ![]() n, there will be a subcollection Bi1, . . . ,Bim of balls that are disjoint, but that nevertheless contain a significant fraction of the volume covered by the original balls. To be precise, one can choose the disjoint balls so that
n, there will be a subcollection Bi1, . . . ,Bim of balls that are disjoint, but that nevertheless contain a significant fraction of the volume covered by the original balls. To be precise, one can choose the disjoint balls so that

(The constant 5-n can be improved, but this will not concern us here.) This result is obtained by a “greedy algorithm”: one picks balls one by one, at each stage choosing the largest ball among the Bj that is disjoint from all the balls already selected.
One consequence of the Vitali covering lemma is the Hardy-Littlewood maximal inequality, which we will briefly describe. Given any function f ∈ L1(![]() n), any x ∈
n), any x ∈ ![]() n, and any r > 0, we can calculate the average of |f| in the n-dimensional sphere B(x, r) of center x and radius r. Next, we can define the maximal function F of f by letting F(x) be the largest of all these averages as r ranges over all positive real numbers. (More precisely, one takes the supremum.) Then, for each positive real number λ one can define a set Xλ to be the set of all x such that F(x) > λ. The Hardy-Littlewood maximal inequality asserts that the volume of Xλ is at most 5n ||f|| L1/λ.2
n, and any r > 0, we can calculate the average of |f| in the n-dimensional sphere B(x, r) of center x and radius r. Next, we can define the maximal function F of f by letting F(x) be the largest of all these averages as r ranges over all positive real numbers. (More precisely, one takes the supremum.) Then, for each positive real number λ one can define a set Xλ to be the set of all x such that F(x) > λ. The Hardy-Littlewood maximal inequality asserts that the volume of Xλ is at most 5n ||f|| L1/λ.2
To prove it, one observes that Xλ can be covered by balls B(x, r) on each of which the integral of |f| is at least λ vol(B(x,r)). To this collection of balls one can then apply the Vitali covering lemma, and the result follows. The Hardy-Littlewood maximal inequality is a quantitative result, but it has as a qualitative consequence the Lebesgue differentiation theorem, which asserts the following. If f is any absolutely integrable function defined on ![]() n, then for almost every x ∈
n, then for almost every x ∈ ![]() n the averages
n the averages
![]()
of f over the Euclidean balls about x tend to f(x) as r → 0. This example demonstrates the importance of the underlying geometry (in this case, the combinatorics of metric balls) in harmonic analysis.
Further Reading
Stein, E. M. 1970. Singular Integrals and Differentiability Properties of Functions. Princeton, NJ: Princeton University Press.
——. 1993. Harmonic Analysis. Princeton, NJ: Princeton University Press.
Wolff, T. H. 2003. Lectures on Harmonic Analysis, edited by I. Łaba and C. Shubin. University Lecture Series, volume 29. Providence, RI: American Mathematical Society.
2. This version of the Hardy-Littlewood inequality looks somewhat different from the one mentioned briefly in the previous section, but one can deduce that inequality from this one by the real interpolation method discussed earlier.
1. Strictly speaking, this sentence describes the field of real-variable harmonic analysis. There is another field called abstract harmonic analysis, which is primarily concerned with how real- or complex- valued functions (often on very general domains) can be studied using symmetries such as translations or rotations (for instance, via the Fourier transform and its relatives); this field is of course related to real-variable harmonic analysis, but is perhaps closer in spirit to representation theory and functional analysis, and will not be discussed here.
