V.12 The Four-Color Theorem

Bojan Mohar

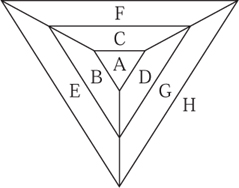
The four-color theorem asserts that the regions of any map drawn in the plane (or, equivalently, on the two-dimensional sphere) can be colored with no more than four colors in such a way that any two regions with a common boundary are given different colors. The example in figure 1 shows that four distinct colors are necessary since the regions A, B, C, and D are all adjacent to each other. This result was conjectured by Francis Guthrie in 1852. An incorrect proof was given by Kempe in 1879, and for eleven years the problem was believed to have been solved, until Heawood pointed out the error in 1890. However, Heawood showed that Kempe’s basic idea, which we shall outline below, could at least be used to give a correct proof that five colors were always sufficient. After that, the problem became a famous example of a question that remained stubbornly open despite being very easy to understand. (Another such problem was FERMAT’S LAST THEOREM [V.10].)

In modern mathematics, map-coloring problems are usually formulated in the language of graph theory. To any map we assign a GRAPH [III.34]: the vertices of the graph correspond to the regions of the map, and we declare two vertices to be adjacent if the corresponding regions share a piece of their boundary. The graph for the map in figure 1 is shown in figure 2. It is easy to see that the graph of any map in the plane can be drawn in such a way that no two edges cross each other: such graphs are called planar. Instead of coloring regions of maps, we now color vertices of the corresponding graphs. If no two vertices that are joined by an edge have the same color, then we say that the coloring is proper. After this reformulation, the four-color theorem states that every planar graph G has a proper coloring with at most four colors.

Figure 1 A map with eight regions.

Here, briefly, is the proof of the five-color theorem due to Kempe and Heawood. It is a proof by contradiction, so we start by assuming that the result is false. If that is the case, then there must be a graph G of minimal size that has no proper coloring with five colors. EULER’S FORMULA [I.4 §2.2] says that V - E + F = 2 for any (connected) planar graph, where V is the number of vertices, E is the number of edges, and F is the number of regions into which the plane is divided by any drawing of the graph. It is not hard to deduce from this formula that G has a vertex v with at most five neighbors (that is, other vertices linked to v by an edge) in the graph. If we remove v from the graph, then we can find a proper coloring of what is left, because G is a minimal counterexample to the theorem. If v has fewer than five neighbors, then we can color v as well, since there are at most four colors that need to be avoided and we have five colors at our disposal. So the only thing that can go wrong is if v has five neighbors and those five colors all get different colors when we color the rest of G.

Let us suppose that the colors of the neighbors of v are red, yellow, green, blue, and brown, as we go clockwise around v. As it stands, we cannot color v, but we could try to do so by adjusting the coloring of the rest of the graph. For instance, we could try recoloring the red vertex green, thereby freeing up red to be used for v. Of course, if we did that we might have to recolor further vertices, but we could try to find a recoloring as follows: first change the color of the red neighbor of v to green. Then change all the green neighbors of that vertex to red, and all the red neighbors of those vertices to green, and so on. When we have finished this process, the one thing that could go wrong is that we might end up recoloring the green neighbor of v red, in which case we would not after all be free to use red for v. This will happen if and only if there is a chain of vertices from the red neighbor of v to the green neighbor that alternates red and green. However, if this circumstance arises, we can try to recolor the yellow neighbor of v blue in a similar way. Once again, the only thing that can stop us is an alternating chain of yellow and blue vertices going from the yellow neighbor of v to the blue neighbor. But such a chain cannot exist, as it would at some point have to cross the red/green chain, and this contradicts the fact that the graph is planar.

Figure 2 The graph of the map from figure 1.

Returning to the four-color problem, the German mathematician Heinrich Heesch proposed a general method for tackling it that can be thought of as a more complicated version of the above argument. The idea is to identify a list C of “configurations” with the following properties. First, every planar graph must contain a configuration X that belongs to C. Second, given a planar graph G that contains a configuration X from C, and given a proper coloring of the rest of G that uses at most four colors, it is possible to adjust this coloring in such a way that it can be extended to a proper coloring of the whole of G. In the proof of the five-color theorem above, there was a very simple list of five configurations: a vertex v with one edge, two edges, three edges, four edges, or five edges coming out of it. Nothing this simple works for the four-color problem, but Heesch’s idea was that it might be possible to solve the problem by using a more complicated list of configurations.

Such a list was found by Kenneth Appel and Wolfgang Haken in 1976. However, this is by no means the whole story, because the list of configurations that they found was not just “more complicated” but so much more complicated that it broke new ground: it was the first time that a major theorem had been proved with a proof that was too long to be humanly checkable. The reason for this was partly that their list C contained about 1200 configurations, but a more important reason was that for some configurations X it was necessary to check hundreds of thousands of cases in order to demonstrate that a coloring of the rest of the graph could be adjusted to accommodate a coloring of X as well. Therefore, there was no alternative but to use a computer to do the checking. (Heesch had himself proposed a list, but some of his configurations would have involved so many cases that even a computer could not have checked them all.)

The reaction of other mathematicians to the proof of Appel and Haken was mixed. Some hailed it as the addition of a powerful new tool to the mathematical armory. Others were uneasy about having to trust that the relevant computer program had been written correctly and that the computer had operated as it should. And in fact the proof turned out to have several flaws, though all those that were discovered were subsequently corrected by Appel and Haken in their monograph of 1989. Any doubts there may have been of this kind were removed once and for all in 1997, when Robertson, Sanders, Seymour, and Thomas developed another proof based on similar principles. The part of the proof that was checkable by humans was made more transparent, and the computer-verified part was supported by a well-structured collection of data that enabled the proofs to be checked independently. One could still question whether the compilers used were correct and whether the hardware was stable, but the proof has been checked on different platforms, using different programming languages and operating systems, so this proof is much less likely to be incorrect than a typical human-checked proof of even moderate length.

The result is that very few mathematicians are now worried about whether the proof is correct. However, there are many who object to it for a different reason. Even if we can now be certain that the theorem is true, we can still ask why it is true, and not everybody regards the answer “Because hundreds of thousands of cases were checked and they all turned out to be OK” as a satisfactory explanation. As a result, if someone were to discover a shorter and more accessible proof it would be regarded by many as a breakthrough comparable to the solution of the problem by Appel and Haken. An unfortunate side effect of this is that mathematics departments around the world still receive many incorrect attempted proofs, several of which repeat the mistake of Kempe.

Like many good problems, the four-color problem provoked the development of many important new mathematical ideas. The theory of graph colorings, in particular, has evolved into a deep and beautiful area of research. (See EXTREMAL AND PROBABILISTIC COMBINATORICS [IV.19 §2.1.1] and also Jensen and Toft (1995).) Extensions of map-coloring problems to arbitrary surfaces led to the development of topological graph theory, and questions about the planarity of graphs culminated in the theory of GRAPH MINORS [V.32].

One of the most prolific graph theorists, William T. Tutte, judged the impact of the four-color theorem on mathematics by proclaiming: “The four-colour theorem is the tip of the iceberg, the thin end of the wedge, and the first cuckoo of Spring.”

Further Reading

Appel, K., and W. Haken. 1976. Every planar map is four colorable. Bulletin of the American Mathematical Society 82:711–12.

———. 1989. Every Planar Map Is Four Colorable. Contemporary Mathematics, volume 98. Providence, RI: American Mathematical Society.

Jensen, T., and B. Toft. 1995. Graph Coloring Problems. New York: John Wiley.

Robertson, N., D. Sanders, P. Seymour, and R. Thomas. 1997. The four-colour theorem. Journal of Combinatorial Theory B 70:2–44.