III.22 The Euclidean Algorithm and Continued Fractions
Keith Ball
1 The Euclidean Algorithm
THE FUNDAMENTAL THEOREM OF ARITHMETIC [V.14], which states that every integer can be factored into primes in a unique way, has been known since antiquity. The usual proof depends upon what is known as the Euclidean algorithm, which constructs the highest common factor (h, say) of two numbers m and n. In doing so, it shows that h can be written in the form am + bn for some pair of integers a, b (not necessarily positive). For example, the highest common factor of 17 and 7 is 1, and sure enough we can express 1 as the combination 1 = 5 × 17 - 12 × 7.
The algorithm works as follows. Assume that m is larger than n and start by dividing m by n to yield a quotient q1 and a nonnegative remainder rl that is less than n. Then we have
Now since rl < n we may divide n by rl to obtain a second quotient and remainder:
Continue in this way, dividing rl by r2, r2 by r3, and so on. The remainders get smaller each time but cannot go below zero. So the process must stop at some point with a remainder of 0: that is, with a division that comes out exactly. For instance, if m = 165 and n = 70, the algorithm generates the sequence of divisions
The process guarantees that the last nonzero remainder, 5 in this case, is the highest common factor of m and n. On the one hand, the last line shows that 5 is a factor of the previous remainder 20. Now the last-butone line shows that 5 is also a factor of the remainder 25 that occurred one step earlier, because 25 is expressed as a combination of 20 and 5. Working back up the algorithm we conclude that 5 is a factor of both m = 165 and n = 70. So 5 is certainly a common factor of m and n.
On the other hand, the last-but-one line shows that 5 can be written as a combination of 25 and 20 with integer coefficients. Since the previous line shows that 20 can be written as a combination of 70 and 25 we can write 5 in terms of 70 and 25:
5 = 25 - 20 = 25 - (70 - 2 × 25) = 3 × 25 - 70.
Continuing back up the algorithm we can express 25 in terms of 165 and 70 and conclude that
5 = 3 × (165 - 2 × 70) - 70 = 3 × 165 - 7 × 70.
This shows that 5 is the highest common factor of 165 and 70 because any factor of 165 and 70 would automatically be a factor of 3 × 165 - 7 × 70: that is, a factor of 5. Along the way we have shown that the highest common factor can be expressed as a combination of the two original numbers m and n.
2 Continued Fractions for Numbers
During the 1500 years following Euclid, it was realized by mathematicians of the Indian and Arabic schools that the application of the Euclidean algorithm to a pair of integers m and n could be encoded in a formula for the ratio m/n. The equation (1) can be written
where F = n/r1. Now equation (2) expresses F as
The next step of the algorithm will produce an expression for r1/r2 and so on. If the algorithm stops after k steps, then we can put these expressions together to get what is called the continued fraction for m/n:
For example,
The continued fraction can be constructed directly from the ratio 165/70 = 2.35714 . . . without reference to the integers 165 and 70. We start by subtracting from 2.35714 . . . the largest whole number we can: namely 2. Now we take the reciprocal of what is left: 1/0.35714 . . . = 2.8. Again we subtract off the largest integer we can, 2, which tells us that q2 = 2. The reciprocal of 0.8 is 1.25, so q3 = 1 and then, finally, 1/0.25 4, so q4 = 4 and the continued fraction stops.
The mathematician John Wallis, who worked in the seventeenth century, seems to have been the first to give a systematic account of continued fractions and to recognize that continued-fraction expansions exist for all numbers (not only rational numbers), provided that we allow the continued fraction to have infinitely many levels. If we start with any positive number, we can build its continued fraction in the same way as for the ratio 2.35714 . . . . For example, if the number is π = 3.14159265 . . . , we start by subtracting 3, then take the reciprocal of what is left: 1/0.14159 . . . = 7.06251 . . . . So for π we get that the second quotient is 7. Continuing the process we build the continued fraction
The numbers 3, 7, 15, and so on, that appear in the fraction are called the partial quotients of π.
The continued fraction for a real number can be used to approximate it by rational numbers. If we truncate the continued fraction after several steps, we are left with a finite continued fraction which is a rational number: for example, by truncating the fraction (7), one level down we get the familiar approximation π ≈ 3 + 1/7 = 22/7; at the second level we get the approximation 3 + 1/(7 + 1/15) = 333/106. The truncations at different levels thus generate a sequence of rational approximations: the sequence for π begins
3, 22/7, 333/106, 355/113, . . . .
Whatever positive real number x we start with, the sequence of continued-fraction approximations will approach x as we move further down the fraction. Indeed, the formal interpretation of the equation (7) is precisely that the successive truncations of the fraction approach π.
Naturally, in order to get better approximations to a number x we need to take more “complicated” fractions—fractions with larger numerator and denominator. The continued-fraction approximations to x are best approximations to x in the following sense: if p/q is one of these fractions, then it is impossible to find any fraction r/s that is closer than p/q to x and that has denominator s smaller than q.
Moreover, if p/q is one of the approximations coming from the continued fraction for x, then the error x - p/q cannot be too large relative to the size of the denominator q; specifically, it is always true that
This error estimate shows just how special the continued-fraction approximations are: if you pick a denominator q without thinking, and then select the numerator p that makes p/q closest to x, the only thing you can guarantee is that x lies between (p - 1/2) /q and (p +1/2)/q. So the error could be as large as 1/(2q), which is much bigger than 1/(q2) if q is a large integer.
Sometimes a continued-fraction approximation to x can have even smaller error than is guaranteed by (8). For example, the approximation π ≈ 355/113 that we get by truncating (7) at the third level is exceptionally accurate, the reason being that the next partial quotient, 292, is rather large. So we are not changing the fraction much by ignoring the tail 
. In this sense, the most difficult number to approximate by fractions is the one with the smallest possible partial quotients, i.e., the one with all its partial quotients equal to 1. This number,
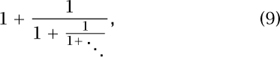
can be easily calculated because the sequence of partial quotients is periodic: it repeats itself. If we call the number φ, then φ - 1 is 
. The reciprocal of this number is exactly the continued fraction (9) for φ. Hence
which in turn implies that φ2 - φ = 1. The roots of this quadratic equation are (1 + 
)/2 = 1.618 . . . and (1 - )/2 = -0.618 . . . . Since the number we are trying to find is positive, it is the first of these roots: the so-called golden ratio.
It is quite easy to show that, just as (9) represents the positive solution of the equation x2 - x - 1 = 0, any other periodic continued fraction represents a root of a quadratic equation. This fact seems to have been understood already in the sixteenth century. It is quite a lot trickier to prove the converse: that the continued fraction of any quadratic surd is periodic. This was established by LAGRANGE [VI.22] during the eighteenth century and is closely related to the existence of units in quadratic NUMBER FIELDS [III.63].
3 Continued Fractions for Functions
Several of the most important functions in mathematics are most easily described using infinite sums. For example, the EXPONENTIAL FUNCTION [III.25] has the infinite series
There are also a number of functions that have simple continued-fraction expansions: continued fractions involving a variable like x. These are probably the most important continued fractions historically.
For example, the function x → tanx has the continued fraction
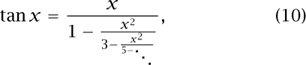
valid for any value of x other than the odd multiples of π/2, where the tangent function has a vertical asymptote.
Whereas the infinite series of a function can be truncated to provide polynomial approximations to the function, truncation of the continued fraction provides approximations by rational functions: functions that are ratios of polynomials. For instance, if we truncate the fraction for the tangent after one level, then we get the approximation
This continued fraction, and the rapidity with which its truncations approach tan x, played the central role in the proof that π is irrational: that π is not the ratio of two whole numbers. The proof was found by Johann Lambert in the 1760s. He used the continued fraction to show that if x is a rational number (other than 0), then tan x is not. But tan π /4 = 1 (which certainly is rational), so π/4 cannot be.