V.27 Problems and Results in Additive Number Theory

Is every even number greater than 4 the sum of two odd primes? Are there infinitely many primes p such that p + 2 is also a prime? Is every sufficiently large positive integer the sum of four cubes? These three questions are all famous unsolved problems in number theory: the first is called the Goldbach conjecture, the second is the twin prime conjecture (discussed in some detail in ANALYTIC NUMBER THEORY [IV.2]), and the third is a special case of Waring’s problem, which we shall discuss later.

These three problems belong to an area of mathematics known as additive number theory. In order to say in general terms what this area is, it is useful to make some simple definitions. Suppose that A is a set of positive integers. Then the sumset of A, denoted A + A, is the set of all x + y such that x and y (which are allowed to be equal) both belong to A. For example, if A is the set {1, 5, 9, 10, 13}, then A + A is the set {2, 6, 10, 11, 14, 15, 18, 19, 20, 22, 23, 26}. Similarly, the difference set, denoted A-A, is the set of all x - y such that x and y both belong to A. In the above example, A - A = {-12, -9, -8, -5, -4, -3, -1, 0, 1, 3, 4, 5, 8, 9, 12}.

Using this language, we can state two of our three problems very succinctly. Let P be the set of all odd primes and let C be the set of all cubes. Then Goldbach’s conjecture is the statement that P + P is the set {6, 8, 10, 12, . . . }, and the special case of Waring’s problem asks whether every sufficiently large integer belongs to C + C + C + C. The twin prime conjecture is slightly more complicated: it states not just that 2 belongs to the set P - P but that it does so “infinitely many times.” (In a similar way, if A is the set in the previous paragraph, then A - A contains the number 4 three times.)

These problems are notoriously difficult. However, remarkably, there are some closely related problems that look just as hard at first, but which have been solved. For instance, Vinogradov’s three-primes theorem is the statement that every sufficiently large odd integer is the sum of three odd primes. Without the “sufficiently large” this would answer the ternary Goldbach problem, which asks whether every odd number from 9 onward is a sum of three odd primes. (How large is “sufficiently large”? Well, until recently you needed your number to have about 7 000 000 digits, but in 2002 this was reduced to under 1500 digits.) As for Waring’s problem, it is known that every sufficiently large positive integer is a sum of seven cubes. More generally, it seems likely that, for any k, every sufficiently large integer can be written as a sum of at most 100k kth powers (where 100 is just a randomly chosen largish number—it is possible that even 4k kth powers are enough), and although a proof of this is well beyond today’s mathematical technology, it has been shown that a little over k logk kth powers are enough. Since log k is a very slowly growing function, this result is, in a certain sense, not too far from a solution to the problem.

How does one obtain results such as these? Some of the proofs are pretty complicated, so we cannot give a full answer here. However, we can at least explain one idea that is fundamental to many of the arguments, namely the use of exponential sums. Let us illustrate it by looking at the beginning of the proof of the Vinogradov three-primes theorem.

Imagine, then, that we have a very large odd integer n and we wish to prove that it is a sum of three odd primes. Here is an argument that strongly suggests that our task is impossible: if n is over three times larger than the largest known prime, as it may very well be, then we cannot produce three primes that add up to n without finding a new prime. Indeed, we could take n to be astronomically large, + 1, say, and then n would be far beyond any prime that has ever been discovered or is ever likely to be discovered.

This argument is, however, flawed, and the clue to what is wrong with it lies in the word “produce.” We do not have to produce the three primes to show that they exist, any more than Euclid had to specify an infinite sequence of primes in order to show that there were infinitely many. (For a proof that there are, see [IV.2 §2].) But, one might ask, what alternative could there possibly be to actually finding three odd primes that add up to n?

This question has a beautifully simple answer: we shall attempt to count, or rather estimate, the number of triples p₁, p₂, p₃ of odd primes such that p₁ + p₂ + p₃ = n. If the estimate we manage to obtain is rather large, and if in addition we can show that it is reasonably accurate, then the actual number of such triples must also be rather large. This will imply that there is such a triple, and will not require us to “produce” one.

However, our answer immediately raises a difficult-looking question: how do we estimate the number of such triples? This is where exponential sums come in. We shall use certain properties of the EXPONENTIAL FUNCTION [III.25] to reformulate our counting problem as a problem about estimating a certain integral.

As is customary in this area, let us write e(x) instead of e^2πi1 The two basic properties that we shall use of the function e(x) are that e(x + y) = e(x)e(y) and that e(nx) dx = 1 if n = 0, and 0 if n is any other integer. Let us also adopt the convention that if we write ∑_p≤n, then we are summing over all odd primes less than or equal to n. Now define a function F(x) by the formula F(x). That is,

F(x) = e(3x) + e(5x) + e(7x) + e(11x) + . . . + e(qx),

where q is the largest prime less than or equal to n. This is a sum of exponentials—hence the phrase “exponential sums.” Next, we consider the cube of this function:

F(x)³ = (e(3x) + e(5x) + e(7x) + . . . + e(qx))³

When we multiply out the right-hand side, we obtain the sum of all terms of the form e(p₁x)e(p₂x)e(p₃x), where p₁, p₂, and p₃ are primes between 3 and q.

The integral we shall look at is F(x)³e(-nx) dx. From our discussion in the previous paragraph, we know that this will be the sum of all integrals of the form e(p₁x)e(p₂x)e(p₃x)e(-nx) dx. Now the first basic property of e(x) tells us that this last integral is equal to e((p_l + p₂ + p₃ - n)x) dx, and the second one then tells us that it is 1 if p₁ + p₂ + p₃ = n and 0 otherwise. Therefore, when we sum over all possible triples p₁, p₂, p₃ of odd primes less than or equal to n, we get a contribution of 1 for each triple that adds up to n and 0 for all other triples. In other words, the integral F(x)³e(-nx) dx exactly equals the number of ways of writing n as a sum of three odd primes.

This “reduces” our problem to that of estimating the integral F(x)³e(-nx) dx. But the function F(x) looks rather difficult to analyze. Is it really feasible to estimate an expression such as , which mixes prime numbers with exponentials?

Surprisingly, it is. The details are complicated, but the fact that it can be done becomes less mysterious after one thinks for a moment about which exponential sums we definitely can estimate. Are there at least some sets A of integers for which we can handle sums of the form Yes there are: arithmetic progressions. Suppose A is the set {s,s + d, s + 2d,. . . , s + (m - 1)d}: that is, the arithmetic progression of length m and common difference d that starts at s. Then, using the basic properties of e(x), we find that is

e(sx) + e((s + d)x) + . . . + e((s + (m - 1)d)x)

= e(sx) + e(dx)e(sx) + . . . + e((m - 1) dx)e(sx)

= e(sx)(1 + e(dx) + e(dx)² + . . . + e(dx)^m-1)

This last expression is the sum of a geometric progression that starts at e(sx) and has common ratio e(dx). Using the standard formula and the basic properties of e(x), we deduce that

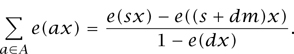
Such expressions are useful because they can often be shown to be small. Suppose, for instance, that |1 - e(dx)| is at least as big as sonic constant c. We know that |e(sx) - e((s + dm)x)| ≤ 2, so the modulus of the right-hand side is at most 2/c. If c is not too small, then this shows that there is a huge amount of cancellation in the sum : we added together m numbers of modulus 1 and obtained a number of modulus no bigger than 2/c.

For certain values of x, we can use this simple observation to help us estimate the sum . What we need to do is express the sum over P as a combination of sums over arithmetic progressions, and this is a very natural thing to do, since P consists of all those integers up to n that do not lie in certain arithmetic progressions (such as 14, 21, 28, 35, 42, . . .). So we can begin by taking the sum = 1 ^e(tx). From this we need to subtract the contribution from all even integers, which is ∑_t≤n/2^e(2tx). We also need to subtract the contribution from multiples of 3, apart from 3 itself. This contribution is ∑_1≤t/3^e(3tx). Now we find that we have subtracted the contribution from multiples of 6 twice, so we correct for that by adding ∑_t≤n/6^e(6tx).

This process can be continued, and it leads to a way of decomposing the sum over primes into a combination of sums over geometric progressions. If x is not close to a rational with small denominator, then most of the common ratios are far from 1, so most of the sums over progressions are small. Unfortunately, there are too many of them for this simple argument to lead to a useful estimate. However, there is a more sophisticated argument with a similar flavor that does.

What happens if x is close to a rational with small denominator? For example, what can we say about the sum ∑_p≤n^e(p/3)? Here we use more direct methods: it is known that roughly half of all primes are 1 (mod 3) and half are 2 (mod 3) (see [IV.2 §4]), which tells us that this sum is roughly (|P|/2)(e(p/3) + e(2p/3)), where |P| denotes the size of the set P.

For very similar reasons, in Waring’s problem one finds oneself wanting to know about exponential sums such as G(x) = . Again, one can sometimes estimate these by reducing them to sums of geometric progressions. This is easiest to show in the case k = 2. The idea is to look not at G(x) directly but at |G(x)|², which a moment’s calculation shows is equal to . Now t² - u² = (t + u)(t - u), so we can change variables, setting ν = t + u and = t - u. This gives us the sum ∑_(v,w)∈v^e(νx), where V is the set of all (ν, ) such that (ν + )/2 and (ν + )/2 (which equal t and u, respectively) are both between 0 and m. For each ν the set of possible values of is an arithmetic progression, so we have decomposed |G(x)|² into a sum of sums of geometric progressions, one for each ν.

So far we have been looking at so-called direct problems in additive number theory. These are problems where one specifies a set and then tries to understand its sumset or difference set. We have only scratched the surface of the subject: other related results and techniques are discussed in [IV.2] (see in particular sections 7, 9, and 11).

Direct problems have a long history, but in recent years another class of problems, called inverse problems, have become an important focus of research as well. These concern the following broad question: if you are given information about a sumset or a difference set, what can you deduce about the original set? We end by describing one of the highlights of this kind of additive number theory, called Freiman’s theorem.

It is not hard to prove that if A is any set of integers of size n, then the size of A + A must be between 2n - 1 and n(n + 1)/2. (The first happens if A is an arithmetic progression and the second happens if all the sums you can make are different.) What can we say about A if the size of A + A is at most 100n, or, more generally, is at most Cn for some constant C that remains fixed as n tends to infinity?

Suppose that we can find an arithmetic progression P of size at most 50n such that A is a subset of P. Then A + A is a subset of P + P, which has size at most 100n - 1. So if A is two percent of an arithmetic progression, then A + A has size at most 100n. However, there are other ways of producing such sets. Suppose, for instance, that A consists of all numbers of up to seven digits such that the third, fourth, and fifth digits from the end are 0: that is, numbers such as 3500026 or 99 000 90. There are 100 × 100 = 10 000 of these. If we add two of them together, then we get a number like 138 00162 or 14100 068, which is made up of a number between 0 and 198, followed by two 0s, followed by a second number between 0 and 198 (written with 0s, in front if these are needed to make it up to three digits). There are 199 × 199 of these, which is less than 40000. Therefore, the size of A + A is less than four times the size of A. However, A does not fill up two percent of any arithmetic progression P: such a progression would have to have common difference 1 and include both the numbers 0 and 99 000 99, and 10 000 is nothing like two percent of 9 900100.

However, A is a very structured set: it is an example of a two-dimensional arithmetic progression. Roughly speaking, an ordinary, or one-dimensional, arithmetic progression is one that you build up by starting with a number s and repeatedly adding another one, d, called the common difference. You build up a two- dimensional arithmetic progression by using two “common differences” d/₁ and d₂. That is, you have a starting number s and you look at numbers of the form s + ad₁ + bd₂, specifying that a should be between 0 and m₁ - 1 and b should be between 0 and m₂ - 1. Our set A is a two-dimensional progression with s = 0, d₁, d₂ = 100000, and m₁ = m₂ = 100.

In a similar way one can define higher-dimensional progressions. It is not hard to show that if P is an r-dimensional progression, then the size of P + P is less than 2^r times the size of P. Therefore, if A is a subset of P and the size of P is at most C times the size of A, then the size of A + A is at most the size of P + P, which is at most 2^r C times the size of A.

This tells us that if A is a large subset of a low- dimensional arithmetic progression, then A has a small sumset. Freiman’s theorem is the remarkable statement that these are the only sets with small sumsets. That is, if A + A is not much larger than A, then there must be some low-dimensional arithmetic progression P that contains A and is not much bigger than A. Exponential sums are vital for the proof of this theorem as well. Freiman’s theorem has had many applications, and is likely to have many more.