VII.13 Mathematics and Music

Catherine Nolan

1 Introduction and Historical Overview

Music is the pleasure the human mind experiences from counting without being aware that it is counting.

This intriguing remark of LEIBNIZ [VI.15], from a 1712 letter to fellow mathematician CHRISTIAN GOLDBACH [VI.17], suggests a serious connection between mathematics and music, two subjects—one a science, the other an art—that may at first seem very different from each other. Leibniz was perhaps thinking of the longstanding historical and intellectual association of the two disciplines that date back to the time of PYTHAGORAS [VI.1], when the subject of music was part of an elaborate classification scheme of knowledge in the mathematical sciences. This scheme became known in the Middle Ages as the quadrivium, and consisted of the four disciplines of arithmetic, music (harmonics), geometry, and astronomy. In the Pythagorean world-view, these subjects were interlinked, since in one way or another they were all concerned with simple ratios. Music was merely the aural manifestation of a more universal harmony, which was likewise expressed by relationships between numbers, geometrical magnitudes, or the motions of celestial bodies. Harmonic consonance of musical intervals resulted from simple ratios of the first four natural numbers, 1:1 (the unison), 2:1 (the octave), 3:2 (the perfect fifth), and 4:3 (the perfect fourth), and was demonstrated empirically by the ratios of lengths of vibrating strings on the ancient instrument the monochord.¹ Beginning with the Scientific Revolution of the seventeenth century, theories of tuning and temperament of musical intervals required more advanced mathematical ideas as well, such as logarithms and decimal expansions.

Musical composition has been inspired by mathematical techniques throughout its history, although mathematically inspired compositional techniques are associated mainly with music of the twentieth, and now twenty-first, centuries. A striking early example appears in the section on melody in a monumental treatise on music, entitled Harmonie universelle (1636–37), by the mathematician Marin Mersenne. Mersenne applied simple (from today’s perspective) combinatorial techniques to the distribution and organization of notes in melodies. For example, he calculated the number of different arrangements or permutations of n notes, for each n between 1 and 22 (twenty-two notes delimiting the range of three octaves). The answer is of course n!, but in his zeal to illustrate this, he notated on musical staves all 720 (6!) permutations of the six notes of the minor hexachord (A, B, C, D, E, F), occupying a full twelve pages of Harmonie universelle. He went on to explore more complicated problems such as determining the number of melodies of a certain number of notes selected from a larger number, or determining the number of arrangements of finite collections of notes containing certain numbers of repetitions of one or more notes. He illustrated some of his findings with combinations of letters as well as musical notation, thereby showing that the music was incidental to the problems, which were in essence purely combinatorial. Such exercises, while seemingly of little practical or aesthetic value, at least demonstrated the great musical diversity that was in principle available with only a limited set of resources.

The polymath Mersenne was a composer and practicing musician as well as a mathematician, and his fascination with applying a relatively new mathematical technique to music composition showed a level of interest in abstract connections between mathematics and music that is shared by many music theorists, and to a lesser degree by performing musicians and nonspecialist music enthusiasts. The patterns of music, in particular pitch and rhythm, lend themselves well to mathematical description, and some of them are amenable to algebraic reasoning. In particular, the system of twelve equal-tempered notes is naturally modeled using MODULAR ARITHMETIC [III.58], and this, together with combinatorial arguments, was used in the music theory of the twentieth century. In this article we survey the association of mathematics and music from its concrete representation in sound itself, through its manifestation in the working materials of composers, and finally to its explanatory power in abstract music theory.

2 Tuning and Temperament

The most obvious relationships between mathematics and music appear in acoustics, the science of musical sound, and particularly in the analysis of the intervals between pairs of pitches. With the development of polyphonic music in the Renaissance period, the Pythagorean conception of consonance based on the simple ratios of the integers from 1 to 4 eventually came into conflict with musical practice. The acoustically pure perfect consonances of Pythagorean tuning were well-suited for medieval parallel organum,² but in the fifteenth and sixteenth centuries use was increasingly made of the so-called imperfect consonances, that is, major and minor thirds and their octave inversions, minor and major sixths. In Pythagorean tuning, intervals are derived by successions of perfect fifths, so the corresponding frequency ratios are powers of . In conventional Western music, twelve perfect fifths in succession, C–G–D–A–E–B–F^#–C^#–G^#–D^#–A^#–E^#–B^#, are supposed to equal seven octaves (C = B^#), but this does not work in Pythagorean tuning, since ()¹² does not equal 2⁷. Indeed, a succession of Pythagorean perfect fifths will never result in a whole number of octaves. As it happens, twelve Pythagorean perfect fifths give an interval slightly larger than seven octaves. The difference is a small interval known as the Pythagorean comma, which corresponds to a ratio of ()¹²/2⁷, which is about 1.013643.

Pythagorean tuning was originally conceived in terms of successive single pitches. The problems associated with it start to arise when pitches sound simultaneously. While Pythagorean fifths between simultaneous pitches sound pleasing with their simple 3:2 ratios, Pythagorean thirds and sixths have much more complex ratios that sound harsh to Western ears. These came to be replaced by the simple ratios of just intonation, which are ratios of quite small whole numbers. These ratios were considered “natural” because they reflect the ratios of the natural overtone series.³ The Pythagorean major third, which has the relatively complex ratio of ()⁴/2², or was replaced by the slightly smaller major third of just intonation, which has the much simpler ratio 5:4. The difference between these two intervals is known as the syntonic comma, which corresponds to the ratio 81:80, or 1.0125. Likewise, the Pythagorean minor third has ratio 32:27, and so is slightly smaller than the minor third of just intonation, which has ratio 6:5. The difference is again a syntonic comma. The Pythagorean major and minor sixths, the octave inversions of the thirds, also differ from their just counterparts by a syntonic comma.

Figure 1 Successive intervals in a major scale tuned in just intonation.

Suppose that you want to build a C-major scale in just intonation. You can do it as follows. Start with C and define each other note by the ratio of its frequency to that of C. The subdominant and dominant, that is, F and G, have ratios 4:3 and 3:2, respectively. From these three notes one can build major triads in the ratios 4:5:6. So E, for instance, which belongs to the major triad that starts with C, has ratio 5:4. Similarly, A has ratio 5:3, since it is in a ratio 5:4 with F. With this kind of calculation, one ends up with the scale shown in figure 1, where the fractions now represent the frequency ratios between successive notes. The smaller whole tone (10:9) between notes D and E creates intonation problems for the supertonic triad, D–F–A. While the minor triads on E and A (the mediant and submediant) produce the proportion 10:12:15, the minor triad on D is out of tune. Its fifth, D–A, is a syntonic comma flat, as is its third, D–F, which is in fact a Pythagorean minor third.

Tempering (increasing or decreasing) the size of intervals offered a practical solution to the problems inherent in just intonation by distributing the syntonic comma among the major thirds or the perfect fifths of the scale, thereby compromising the purity of one interval to preserve the purity of another. This practice became known as meantone temperament. Various systems of meantone temperament were put forward in the sixteenth and seventeenth centuries for the tuning of keyboard instruments, the most common of which was quarter-comma meantone temperament. In this system the perfect fifth is lowered by a quarter of a syntonic comma so that the major thirds have the pure ratio 5:4.

A perpetual problem with meantone temperaments is that, while modulation to closely related keys sounds pleasing, modulation to more remote keys sounds out of tune. The system of equal temperament, in which the syntonic comma is distributed evenly among all twelve semitones of the octave, gradually became adopted because it removed the limitations on keys for modulation. The discrepancies between just and equal-tempered intervals are small and easily accepted by most listeners. The ratio of an equal-tempered semitone is , or 1.05946 . . . ; by comparison, a just semitone, with ratio 16:15, is 1.06666 . . . . The ratio of an equal-tempered perfect fifth, seven semitones, is or , which is 1.498307 . . . , whereas a just perfect fifth, with ratio 3:2, is of course 1.5. In equal temperament, one starts from a reference such as the note A, which is usually taken to have frequency 440 Hz.⁴ All other notes have frequencies of the form 440()ⁿ where n is the number of semitones between the note in question and the reference note A. In equal temperament, enharmonic notes such as C^# and are acoustically identical—that is, they share the same frequency. Equal temperament was well-suited for the kind of music that was written from the eighteenth century onward, with its much greater range of modulations and chromatic harmonic vocabulary.

The unit of the cent was defined by A. J. Ellis as the ratio between two pitches separated by one hundredth of an equal-tempered semitone, and became the most commonly used unit for measuring and comparing intervals.⁵ The octave consists, therefore, of 1200 cents. If a and b are two frequencies, then the distance in cents between the corresponding pitches is given by the formula n = 1200 log₂(a/b). (As a check, notice that if a = 2b then one does indeed get the answer n = 1200.)

Microtonal systems based on the equal division of the octave into more than twelve parts were proposed and realized by some composers in the twentieth century, but they have not become widely used in Western music. However, the idea of dividing the octave into equal parts has become fundamental. It means that the notes used are naturally modeled by integers. If one regards two notes an octave apart as “the same,” which makes good musical sense, then one is dividing all notes into twelve EQUIVALENCE CLASSES [I.2 §2.3]. The natural model for these is arithmetic modulo 12. As we shall see later, the symmetries of the group of integers mod 12 are of great musical significance.

3 Mathematics and Music Composition

The association of number and music in acoustics was the result of scientific discovery. Number and music have also been associated through invention and creativity in music composition. Fundamental aspects of the temporal organization of music reflect simple proportional relationships. The basic durational values in Western music notation are the whole note , half note , quarter note , eighth note , etc. These are related to each other by simple multiples or fractions—all powers of 2—and these relationships are reflected in the metric organization of musical time into bars with the same number of beats. Bars or measures are indicated by time signatures such as the simple meters , , or (c), where beats (the in these examples) are typically subdivided into two, or the compound meters , , or , in which beats (the . in these examples) are subdivided into three.

A common device in musical composition, especially counterpoint, is for a melodic theme, or subject, to reappear at half or twice the original speed, techniques known as rhythmic augmentation or diminution, respectively. Figures 2 and 3 show the subjects of two fugues from the second volume of J. S. Bach’s Well-Tempered Clavier: no. 9 in E major, whose subject appears in diminution; and no. 2 in C minor, whose subject appears in augmentation. (The last note of the diminished or augmented subject may not be proportionally related to the original in order to allow a good continuation for the music that follows.)

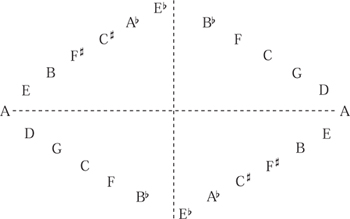
Geometric relations have served as musical resources of other kinds too. A well-known construct in music theory is the circle of fifths, which was originally designed to demonstrate the relationships between different major and minor keys. As illustrated in figure 4, the twelve notes are arranged around the circle as a succession of perfect fifths. Any seven consecutive notes in this circle will be the notes of some major scale, which makes it easy to understand some of the patterns of the key signatures. For instance, the C major scale consists of all the notes from F to B (clockwise). To change from C major to G major, one shifts the sequence by one, losing the note F but gaining F^#. Continuing in this way, we see that C major is the key with no sharps or flats, G major has one sharp, D major has two sharps, A major has three sharps, etc. Similarly, moving counterclockwise from C, F major has one flat, major has two flats, major has three flats, etc. From a mathematical point of view, we have transformed the chromatic scale, which we identify with the additive group of integers mod 12, using the automorphism x 7x, and this makes some musical phenomena much more transparent.

Figure 2 J. S. Bach, Well-Tempered Clavier, Book 2, Fugue no. 9, subject and diminution.

Figure 3 J. S. Bach, Well-Tempered Clavier, Book 2, Fugue no. 2, subject and augmentation.

Reflective symmetry is another geometrical concept with a long history in musical composition. Musicians will frequently describe melodic lines in spatial terms, referring to notes of higher frequencies as “up,” and notes of lower frequencies as “down.” This allows one to think of melodic lines as ascending or descending. Reflection in a horizontal axis interchanges up and down. The musical counterpart to this is known as melodic inversion: one reverses the ascending or descending direction of each interval, and the result is an inverted form of the melody. Figure 5 shows the subject of Fugue no. 23 in B major from the first volume of Bach’s Well-Tempered Clavier and a later appearance of the subject in inverted form. A geometrical reflection is clearly visible in the notation, but, more importantly, the inversion can also be clearly heard in the sound of the music itself.

Figure 4 The circle of fifths.

Figure 5 J. S. Bach, Well-Tempered Clavier, Book 1, Fugue no. 23, subject and inversion.

Conventional Western musical notation implies a two-dimensional organization: the vertical dimension expresses the relative frequency of pitches from low to high, and the horizontal dimension expresses chronological time from left to right. Another compositional device, much rarer than the devices of rhythmic augmentation and diminution or melodic inversion, is that of retrograde, where a melody is played backwards. When the melody is played backwards and forwards simultaneously, the technique is known as a cancrizans canon. Perhaps the best-known examples of cancrizans occur in the music of J. S. Bach, such as in the first canon of The Musical Offering or the first and second canons of the Goldberg Variations. Figure 6 shows the opening and closing measures of the cancrizans from Bach’s Musical Offering. The melody of the first few bars of the upper staff returns in reverse order at the end of the piece in the lower staff, and likewise, the melody of the first few bars of the lower staff returns in reverse order at the end of the upper staff. Joseph Haydn’s Menuetto al rovescio, from the Sonata no. 4 for violin and piano, is another well-known example of a similar technique, in which the first half of the piece is played backwards in the second half.

We may regard the devices of melodic retrograde and inversion as reflections in a two-dimensional musical space. However, retrograde is much more esoteric, owing to the greater constraints involved in the manipulation of musical time. Examples such as those by Bach and Haydn mentioned above demonstrate great ingenuity on the part of the composer, who must make the melodic retrogrades work convincingly with the underlying harmonic progressions. Certain common chord progressions, such as moving from the supertonic to the dominant, do not work well in reverse, so a composer attempting to write a cancrizans canon is forced to avoid them. Similarly, many common melodic patterns do not sound good when reversed. These difficulties account for the rarity of retrograde techniques in tonal music (i.e., music based on major and minor keys). With the abandonment of tonality in the early twentieth century, the main constraints were removed, making composition with retrograde easier. For instance, retrograde and inversion played an important role in serial music, as we shall see. However, composers of such music replaced the traditional constraints of tonal music with others, such as avoiding major or minor triads and bringing out other intervals deemed important for a particular piece.

The atonal revolution in the early twentieth century, during which composers experimented with novel methods of harmonic organization, led to the exploration of new types of symmetry relations in music composition. Scales based on repeating interval patterns (measured in semitones), such as the whole-tone scale (2–2–2–2–2–2) or the octatonic scale (1–2–1–2–1–2–1–2), appealed to composers for the symmetric structures and novel harmonies they embodied. The octatonic scale, also known in jazz circles as the diminished scale, had a particularly wide appeal among a variety of composers of different nationalities, such as Igor Stravinsky, Olivier Messiaen, and Béla Bartók. The novelty of the whole-tone and octatonic scales is that they have nontrivial translational symmetry, a property not shared by the major or minor scales. The whole-tone scale is unchanged if it is transposed by a tone, and the octatonic scale is unchanged if it is transposed by a minor third. There are thus only two distinct translates of the whole-tone scale and three of the octatonic scale. For this reason, neither scale has a clearly defined tonal center, which was a major reason for their attractiveness to early twentieth-century composers.

Figure 6 J. S. Bach, The Musical Offering, opening and closing measures of the cancrizans (canon 1).

Reflective symmetry was used by twentieth-century composers as well, to help them with the formal aspects of compositional design. A fascinating example is the first movement of Bartók’s Music for Strings, Percussion, and Celesta (1936), which extends the traditional principles of the baroque fugue and incorporates a symmetric design. Figure 7 illustrates the structure of the fugue subject entries, starting from the initial entry on A. In a traditional fugue, the subject is stated in tonic, followed by a statement in the dominant, and then again in the tonic (and continuing the alternating pattern of tonic and dominant entries for fugues with more than three voices). In Bartók’s fugue, the first statement of the subject begins with the note A, and the next with E. Instead of returning to A for the third statement, however, the subsequent entries follow a pattern of alternating fifths in opposite directions from A: that is, the sequence A–E–B–F^#, etc., alternates with the sequence A–D–G–C, etc. This pattern is illustrated in figure 7. Each of the interlocked cycles completes a circle of fifths, one clockwise, the other counterclockwise. Each letter in the illustration represents a statement of the fugue subject beginning on that note, and each of the interlocked cycles of fifths arrives on (six semitones from the starting point, A) at its midpoint, so that all twelve notes occur once in the first half of the pattern and once again in the second half. The midpoint of the pattern corresponds to the dramatic climax of the work, after which the pattern of interlocked cycles of fifths resumes with subject entries in inverted form until the conclusion of the work with the return of the subject starting on A.

Figure 7 Plan of fugal entries in Béla Bartók’s Music for Strings, Percussion, and Celesta, first movement (after Morris (1994, p. 61), with permission).

Arnold Schoenberg’s twelve-tone method of composition, which he revealed in the early 1920s, is based on permutations of all the twelve notes, rather than of subsets of seven notes as one has in music in major or minor keys. In twelve-tone music (and atonal music in general), the twelve notes are supposed to have equal prominence: in particular, there is no single note with a special status like that of the tonic in a major or minor key. The basic ingredient of a piece of twelve-tone music is a tone row, which is a sequence given by some permutation of the twelve notes of the chromatic scale. (These notes can, however, be stated in any octave.) Once the tone row has been chosen, it can be manipulated by means of four types of transformation: transposition, inversion, retrograde, and retrograde inversion. Musical transposition corresponds to the mathematical operation of translation: the intervals between successive notes of a transposed row are the same as those between the corresponding notes of the original row, so the entire row is shifted up or down.⁶ Inversion corresponds to reflection, as we have already discussed: the intervals of the row are reflected about a “horizontal” axis. Retrograde corresponds to reflection in time: the row is stated backwards. (However, if it is combined with a transposition, as it may be, then it is better described as a glide reflection.) Retrograde inversion is a composition of two reflections, one vertical and one horizontal: it therefore corresponds to a half turn.

Figure 8 Row forms in Schoenberg’s Suite for Piano (1923).

Figure 8 illustrates the serial transformations applied to a row created by Schoenberg for his Suite for Piano, opus 25, published in 1923. The forms of the row are labeled P (for prime—the original row and its transpositions), R (for retrograde), I (for inversion), and RI (for retrograde inversion). The integers 4 and 10 in the row labels on the left and right refer to the starting notes of the P and I row forms by telling us how many semitones away from C they are. Thus, 4 refers to E (4 semitones above C) and 10 refers to (10 semitones above C). The retrogrades of the P and I forms, R and RI, are labeled on the right-hand side of the figure. It is easy to see the inversion (reflection) of P4 in I4 about the first note E and the transposition of P4 by six semitones in P10, as well as the inversion of P10 about the first note, .

One may wonder what sort of insight we gain from understanding these abstract relationships and why they were so attractive to composers like Schoenberg. In Schoenberg’s Suite, the eight row forms shown in figure 8 are in fact the only ones used in all five movements of the composition. This represents a high degree of selectivity, since there are 48 (= 12 × 4) available row forms. However, this self-imposed restriction is not on its own enough to account for the interest or attraction of this music. An additional aspect of the technique is that the row itself, and the way its transformations unfold in the course of a work, are chosen carefully to bring out certain relationships between notes. For example, all the row forms used in the Suite begin and end on the notes E and , and these notes are frequently articulated in the work so that they take on an anchoring function that fills the void created by the absence of a conventional tonal center. Similarly, the notes in the third and fourth positions in each of the four row forms are always G and , in either order, and likewise these are articulated in various ways in the movements of the Suite so that they can become recognizable. The two pairs of notes just mentioned, E– and G–, are related to each other by sharing the same interval, six semitones (half an octave, also known as the tritone because it spans three whole tones). In the hands of a master composer, a twelve-tone row is not a random collection of notes, but a foundation for an extended composition carefully constructed to produce interesting structural effects that one can learn to recognize and appreciate.

Permutations and serial transformations of other musical parameters besides pitch—such as rhythm, tempo, dynamics, and articulation—were explored by a new generation of postwar European composers, including Olivier Messiaen, Pierre Boulez, and Karlheinz Stockhausen. Compared with the serialization of pitch, however, serialization of these parameters does not lend itself to such precise transformations, because it is less easy to organize them into discrete units than it is the twelve notes of musical space.

It is important to recognize that Schoenberg and most composers whose music exhibits mathematical conceptions such as those we have seen had little if any mathematical training.⁷ Nevertheless, the basic mathematical patterns and relations that we have discussed are so pervasive in so many aspects of so many different kinds of music that the importance of mathematics in music is undeniable.

We end this section with a few more examples. Proportional relations such as the simple ones between note values reappear on a larger scale in relations between lengths of formal divisions in music of Mozart, Haydn, and others: they often use basic building blocks of four-measure phrases and use them in pairs, and pairs of pairs, to form larger units. The techniques of melodic manipulation seen in Bach’s works, which are found in a new guise in Schoenberg’s twelve-tone techniques, can also be found in contrapuntal works of composers before Bach, such as Palestrina. And some composers, including Bach, Mozart, Beethoven, Debussy, Berg, and others, are said to have incorporated numerological elements into their composition, such as symbolic numbers or proportions based on Fibonacci sequences and the golden ratio.

4 Mathematics and Music Theory

In the second half of the twentieth century, the ideas of Schoenberg and his followers were extended and developed in North American music theory. Milton Babbitt, a renowned American composer and theorist, is widely credited with introducing formal mathematics, specifically group theory, to the theoretical study of music. He generalized Schoenberg’s twelve-tone system to any system where one has a finite set of basic musical elements (of which Schoenberg’s twelve-tone rows were just one example), with relations and transformations between them (see Babbitt 1960, 1992). There are forty-eight ways of transforming a row, and Babbitt noted that these transformations form a group, which is in fact the product of the dihedral group D₁₂ with the cyclic group C₂ of two elements. (The D₁₂ in this product is the symmetry group of a dodecagon, and the C₂ allows the time reversal.) The four sets of transformations—P, I, R, and RI (see the previous section)—define a homomorphism from this group to the Klein group C₂ × C₂, by identifying transformations that are equivalent up to rotation.

Figure 9 Circular model of the twelve notes (pitch classes).

Identifying musical notes with the elements of the group ₁₂ of integers mod 12, and modeling various musical operations by means of transformations on this group, makes it much easier to analyze some kinds of music, such as the atonal music of Schoenberg, Berg, and Webern, that do not lend themselves easily to more traditional analysis of harmony (see Forte 1973; Morris 1987; Straus 2005). This identification is illustrated in figure 9. As we have already commented, multiplying by 5 or 7 is an automorphism of ₁₂, and gives the cycle of fifths shown in figure 4 (when one substitutes the mod-12 integers for the names of the notes). This mathematical fact has many musical consequences. One of them is that it is common to substitute fifths by semitones, and vice versa, in chromatic harmony and in jazz.

A branch of music theory known as atonal set theory attempts to give a very general understanding of pitch relations by looking at all the 2¹² = 4096 possible combinations of notes, and defining two such combinations to be equivalent if one can be derived from the other by two simple transformations, the idea being that equivalent combinations will have the same intervals. The transformations in question are transposition and inversion. A transposition up by n semitones (where we think of n as an integer mod 12) is denoted T_n. The notation I is used for a reflection about the note C, so a general inversion takes the form T_nI for some n. (Inversion in this context refers to reflection in musical space, and should not be confused with chord inversion in tonal music.) In these terms, to use a familiar example, the major triad and the minor triad are related to each other by inversion since their successive intervals are reflections of each other (four then three semitones in the major triad and three then four semitones in the minor triad, counting from the lowest note). Consequently, all major and minor triads belong to the same equivalence class. For example, the E-major triad {4, 8, 11} is related to the C-major triad {0, 4, 7} by the transposition T₄ (because {4, 8, 11} ≡ {0+4, 4+4, 7+4}, mod 12), and the G-minor triad {7, 10, 2} is related by inversion to the D-major triad {2, 6, 9} by T₄I (because {7, 10, 2} ≡ {4 − 9, 4 − 6, 4 − 2}, mod 12). An equivalence class, such as the class of major and minor triads, will normally consist of twenty-four sets. However, if it has internal symmetries, such as those of the diminished seventh chord (with interval succession 3–3–3–3) or the whole-tone and octatonic scales mentioned earlier, then the number of sets in the class will be smaller, though it will always be a factor of 24.

Sets of notes in the same equivalence class share certain sonic attributes because they share the same number and types of intervals. But while it seems reasonable enough to regard transposed chords as equivalent, since they really do have an obvious “sameness” in the way they sound, there has been some controversy over the notion of inversional equivalence. For example, is it reasonable to declare major and minor triads to be equivalent to each other when they clearly do not sound the same and have very different musical roles? Of course, we are free to define any equivalence relation we like, so the real question is whether this one has any utility. And in some contexts it does: with sets of notes that do not possess extensive associations with tonal music it is easier to recognize this form of equivalence than it is with major and minor triads. For example, the three notes C, F, and B share the same intervals (one semitone, one perfect fourth or fifth, and one tritone) as the three notes F^#, G, and C^#, and this does indeed give them a noticeable form of “sameness.” (The set {11, 0, 5} is inversionally related to {1, 6, 7} by T₆I because {11, 0, 5} ≡ {6 − 7, 6 − 6, 6 − 1}, mod 12.)

There is other important work in music theory that has been inspired by group theory. The most influential example is David Lewin’s Generalized Musical Intervals and Transformations (1987), which develops a formal theory that connects mathematical reasoning and musical intuition. Lewin generalizes the concept of interval to mean any measurable distance, whether between pairs of pitches, durations, time points, or contextually defined events in a musical work. He develops a model called the generalized interval system (GIS), which consists of a set of musical objects (e.g., pitches, rhythmic durations, time spans, or time points), a group (in the mathematical sense) of intervals (representing the distance, span, or motion between a pair of objects in the system), and a function that maps all possible pairs of objects in the system into the group of intervals. He also uses GRAPH THEORY [III.34] to model musical processes, through his notion of a transformation network. The vertices of such a network are basic musical elements such as melodic lines or chordal roots. These elements come with certain transformations, such as transposition (or shifting by a generalized interval) or the serial transformations from twelve-tone theory. Two vertices are joined by an edge if there is an allowable transformation that takes one to the other. The emphasis thus shifts from the basic elements to the relations that connect them. Transformation networks offer a dynamic way of looking at musical processes, giving visible form to abstract and often nonchronological connections in the analysis of musical works.

The level of generalization and abstraction makes Lewin’s treatise a challenge for the mathematically unsophisticated music theorist, but it does not need more than fairly simple undergraduate-level algebra, so it is accessible enough for the determined reader with some mathematical training. It becomes clear to such a reader that the formality of the presentation is essential to a proper understanding of the transformational approach to music theory and analysis. Despite this formality, Lewin continually maintains contact with music itself, and how his mathematical tools can be applied in different contexts. The result is that the reader is rewarded with insights that would be impossible without the mathematical rigor. Mathematicians, while likely to find the material relatively elementary, may find their attention “captivated by the way in which the author gives new and, sometimes, unexpected interpretations to classical mathematical ideas when applied to musical contexts” (Vuza 1988, p. 285).

5 Conclusion

The playful Leibniz quotation with which this essay began underscores an enduring mathematical presence in music. Both disciplines rely in a fundamental way on concepts of order and reason, as well as more dynamic concepts of pattern and transformation. Music was once subsumed within mathematics, but it has now acquired its own identity as an art that has always derived inspiration from mathematics. Mathematical concepts have provided composers and theorists of music both with tools for creating music and with a language for articulating analytical insights about it.

Further Reading

Babbitt, M. 1960. Twelve-tone invariants as compositional determinants. Musical Quarterly 46:246–59.

——. 1992. The function of set structure in the twelve-tone system. Ph.D. dissertation, Princeton University.

Backus, J. 1977. The Acoustical Foundations of Music, 2nd edn. New York: W. W. Norton.

Forte, A. 1973. The Structure of Atonal Music. New Haven, CT: Yale University Press.

Hofstadter, D. R. 1979. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books.

Lewin, D. 1987. Generalized Musical Intervals and Transformations. New Haven, CT: Yale University Press.

Morris, R. 1987. Composition with Pitch-Classes: A Theory of Compositional Design. New Haven, CT: Yale University Press.

——. 1994. Conflict and anomaly in Bartók and Webern. In Musical Transformation and Musical Intuition: Essays in Honor of David Lewin, edited by R. Atlas and M. Cherlin, pp. 59–79. Roxbury, MA: Ovenbird.

Nolan, C. 2002. Music theory and mathematics. In The Cambridge History of Western Music Theory, edited by T. Christensen, pp. 272–304. Cambridge: Cambridge University Press.

Rasch, R. 2002. Tuning and temperament. In The Cambridge History of Western Music Theory, edited by T. Christensen, pp. 193–222. Cambridge: Cambridge University Press.

Rothstein, E. 1995. Emblems of Mind: The Inner Life of Music and Mathematics. New York: Times Books/Random House.

Straus, J. N. 2005. Introduction to Post-Tonal Theory, 3rd edn. Upper Saddle River, NJ: Prentice Hall.

Vuza, D. T. 1988. Some mathematical aspects of David Lewin’s book Generalized Musical Intervals and Transformations. Perspectives of New Music 26(1):258–87.

1. The monochord was an instrument designed for demonstration, not artistic, purposes. It consisted of a single string stretched between two fixed bridges. A movable bridge between the fixed bridges was used to adjust the length of the string as it was plucked to produce sound, thereby altering the pitch of the sound.

2. Organum is the earliest form of musical polyphony, and involved adding a voice (or voices) to an existing plainchant melody (cantus firmus). In its original form, the added voice proceeded in parallel motion to the plainchant melody at the interval of a perfect fourth or fifth.

3. The partials of the overtone series are multiples of the frequency of the fundamental pitch, and the first six partials generate the intervals of the major triad. For instance, the first six partials of the overtone series of a fundamental pitch C are C(1:1), C(2:1), G(3:1), C(4:1), E(5:1), G(6:1).

4. The frequency of a pitch is a measurement of the number of cycles per second (abbreviated as “cps”). More commonly, the number of cycles per second is identified in units called hertz (abbreviated as “Hz”), named after the physicist Heinrich Rudolf Hertz.

5. Ellis’s account of the cent appeared in his appendix to the eminent nineteenth-century physicist Hermann von Helmholtz’s On the Sensations of Tone (1870; English edn., 1875).

6. Describing transposition as translation does justice to the fact that a melody sounds “the same” when transposed, even though the pitches are different, because the successive intervals are the same. If one arranges the twelve notes in a circle, then one can also think of this translation as a rotation.

7. Some composers, to be sure, have received extended mathematical training, which is reflected in their works. Iannis Xenakis, for example, was trained as an engineer, and had professional contact with the architect Le Corbusier. Xenakis found parallels between music and architecture through his study of Le Corbusier’s Modulor system and its approach to form and proportion based on the human figure. Xenakis’s compositions are characterized by their massive, physical sound and their complex algorithmic processes.