VI.22 Joseph Louis Lagrange
b. Turin, Italy, 1736; d. Paris, 1813
Number theory; algebra; analysis; classical and celestial mechanics
In 1766 Lagrange left his native Turin, where he had been a founding member of what would later become the Turin Academy of Sciences, to become the mathematics director at the Berlin Academy of Sciences. In 1787 he moved to Paris to take up a position as a pensionnaire veteran at the Academy of Sciences. In Paris he also lectured at the École Polytechnique, founded in 1794, and served as one of the members of the committee that established the modern metric system.
Lagrange was only nineteen years old when he wrote to EULER [VI.19] announcing a new formalism to simplify Euler’s method for finding a curve that satisfied an extremum condition. Lagrange’s method was based on the introduction of a new differential operator, δ, to express the independent variations of the coordinates of a curve that produced a local infinitesimal deformation.
Using this formalism he derived the differential equation known today as the Euler-Lagrange equation, the fundamental equation of the CALCULUS OF VARIATIONS [III.94]. Suppose that we wish to find the function y = y(x) that maximizes or minimizes a definite integral of the form
where y′ = dy/dx. The equation states a necessary condition that this function must satisfy:
This is a typical example of Lagrange’s reductionist style. Throughout his career he sought suitable formalisms with which to express and solve the key problems of mathematical analysis.
Lagrange publicly presented his δ-formalism in a memoir published in the second volume (1760-61) of Miscellanea Taurinensia, a review he had helped to found. He coupled this memoir with another in which he used the same formalism to formulate a generalized version of the principle of least action (previously introduced by Maupertuis and Euler). As a result, he was able to derive the equations of motion of any system of distinct bodies attracted by central forces depending on the distances from their centers.
Meanwhile, in the first volume of Miscellanea Taurinensia (1759), Lagrange had published a memoir presenting a new approach to the problem of the vibrating string, where the string is first represented as a discrete system of n particles, and n is then allowed to tend to infinity. Using this method Lagrange argued that Euler was right to allow a large class of “functions,” both “continuous” and “discontinuous,” as solutions of this problem, whereas D′ALEMBERT [VI.20] had maintained that only “continuous functions” (that is, curves expressed by a single equation) could count as solutions.
Lagrange established a very general program in the foundations of classical mechanics in these memoirs. It was based on the interpretation of a continuous system as a limiting case of a discrete one and the use of the method of indeterminate coefficients: supposing that P(x) is a polynomial in x, whose coefficients ai (i = 0, . . . , n) depend on some indetermifates, and that P(x) = 0 for all x (in a given interval), this method consists of deducing the system of equations 
, from which the indeterminates are possibly determined. Lagrange extended this method to sums of polynomials in several (independent) variables, and (following Euler, d’Alembert, and many others) also used it with respect to power series. This program was further elaborated in two memoirs on the motion of the Moon (1764, 1780), and later realized in the Méchanique Analitique (1788). Here, the principle of least action was replaced by a generalization of the Bernoullian principle of “virtual velocities,” which were expressed by variations. Using what are now known as generalized coordinates, ϕi (that is, mutually independent coordinates in the configuration space of a discrete system that characterize completely the position of its bodies), Lagrange derived the equations that are now named after him:
where T and U are the kinetic and potential energy of the system, respectively.
The Méchanique Analitique appeared a century after NEWTON’S [VI.14] Principia and marked the culmination of a purely analytical approach to mechanics. In the preface Lagrange proudly stated that no diagrams would be found in the work and that everything would be reduced to “algebraic operations submitted to a regular and uniform progression.”
Lagrange made fundamental contributions to perturbation theory and THE THREE-BODY PROBLEM [V.33] with research published in the 1770s and 1780s. His methods were further developed by LAPLACE [VI.23] in his Mécanique Céleste and formed the basis for subsequent mathematical work in physical astronomy.
The method of indeterminate coefficients, or rather its extension to power series, is also the crucial technique underlying Lagrange’s approach to the calculus. In a memoir which appeared in the Proceedings of the Berlin Academy (1768) he used it to prove an important result connecting the calculus to the theory of algebraic equations, the so-called Lagrange inversion theorem, which states that a function ϕ(p) of a root p of an equation t - x + ϕ(x) = 0, where ϕ(x) is an arbitrary function of x, can be expanded in a series based on the Taylor expansions of ϕ(t) and ψ(t) (the precise conditions to be satisfied by x, ϕ(x), and ϕ(t) were later clarified by CAUCHY [VI.29] and Roché).
In a memoir of 1772 Lagrange returned to power series and proved that if a function f (x + h) has a power-series expansion in h, then this series can be written in the form
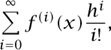
where, for any i, f(i+l) is derived from f(i) in the same way that f′ derives from f. Thus, he just had to prove, through an infinitesimal argument, that f′ = d f / d x to conclude that the only power-series expansion of a function is its Taylor series. In Théorie des Fonctions Analytiques (1797) he then showed (or, rather, claimed to have shown), without making an appeal to the differential calculus, that any function f (x + h) can be expanded in a power series, and suggested interpreting the differential formalism as a formalism that applies to the coefficients of hi/i! in such an expansion. In other words, he suggested defining the differential ratios of any order (that is, the ratios diy/d xi, where y = f (x)) as derivative functions supplying these coefficients, whereas previously these had been thought of as genuine ratios of differentials. He also proved that the remainder of a Taylor series could be written in the form now known as the Lagrange remainder.
The main results obtained by Lagrange within the theory of algebraic equations were presented in a long memoir of 1770 and 1771 in which the formulas for solving equations of degree 2, 3, and 4 were obtained through an analysis of permutations of the roots. This work constituted the starting point for the later researches of ABEL [VI.33] and GALOIS [VI.41]. In the same memoir Lagrange stated a particular but significant case of the theorem in group theory that today bears his name: that the order of a subgroup of a finite group divides the order of the group.
Lagrange also obtained important results in number theory. Arguably the most significant were the proof of a conjecture, advanced by FERMAT [VI.12] (among others) and which Euler had already tried to prove, asserting that any positive integer is the sum of (at most) four squares (1770), and the proof of Wilson’s theorem (first guessed by Wilson and published by WARING [VI.21] without proof), asserting that if n is prime, then (n - 1)! + 1 is divisible by n (1771).
Further Reading
Burzio, F. 1942. Lagrange. Torino: UTET.