IV.16 Mirror Symmetry
Eric Zaslow
1 What Is Mirror Symmetry?
Mirror symmetry is a phenomenon found in theoretical physics that has had profound mathematical applications. It burst onto the mathematical scene after Candelas, de la Ossa, Green, and Parkes exploited the physical phenomenon to make precise predictions about certain sequences of numbers describing geometric spaces. The sequence predicted by those authors began 2875, 609 250, 317 206 375, . . . , and was far beyond the scope of calculation at the time. The phenomenon of mirror symmetry is that some physical theories have equivalent, “mirror” theories that lead to the same predictions. If some prediction requires a hard calculation but is easy to perform in the mirror theory, then you can get the answer for free! These physical theories do not have to be realistic models of physics. For instance, beginning students of physics often study point particles on frictionless planes. Although they are unrealistic, such toy models can bring the physical concepts into focus and their analysis can give rise to very interesting mathematics.
1.1 Exploiting Equivalences
Children at school in the 1950s used log tables to exploit the equivalence of multiplication of positive numbers with addition of real numbers. Given the problem of multiplying two large numbers a and b, they would use a table to look up the logarithms log(a) and log(b) (to a certain number of significant figures), then add them by hand. They would then use the same table to find which number had a logarithm equal to log(a) + log(b). The answer is ab.
College students sometimes exploit the equivalence defined by FOURIER TRANSFORMS [III.27] to solve differential equations. Basically, the Fourier transform is a rule that maps one function f(x) to a new function f (p). What is nice is that the transform of the derivative f′(x) relates in a very simple way to 
(p): it is ip(p), where i is the imaginary number 
. If you want to solve a differential equation such as f′(x) + 2f (x) = h(x), where h(x) is a given function and you are trying to find f, you can map the equation to its Fourier transform equation ip(p) + 2(p) 
(p). This is much easier: it is an algebraic equation rather than a differential equation, and has the solution (p) = (p)/(2 + ip). The solution f (x) is then the function which has (p)/(2 + ip) as its Fourier transform.
Mirror symmetry is like a fancy Fourier transform, mapping much more information than is contained in a single function. Every aspect of a physical theory is involved.
This article will (eventually) focus on the mathematics of mirror symmetry, but it is crucial to understand its physical origins. We therefore begin with a brief guide to physics. (For a further discussion of mathematical physics, see VERTEX OPERATOR ALGEBRAS [IV.17 §2].) This is in no way an adequate treatment—a separate Companion to Physics would be needed—but we hope to give enough of the flavor of the subject to help the reader with the later sections. (A reader familiar with physical theories may wish to skip the next section and refer back as needed.)
2 Theories of Physics
2.1 Formulations of Mechanics and Action Principles
2.1.1 Newtonian Physics
Newton’s second law states that a particle moving through space accelerates1 in proportion to the force it experiences: F = m
. The force is itself the (negative) gradient of a gravitational potential V(x), so this equation can be written m + ∇V(x) = 0. Stationary particles sit at minima of the potential: examples are a ball in equilibrium at the end of a spring, or a pea at the bottom of a bowl. In stable situations, there is a restoring force proportional to some displacement distance. This means that in some appropriate coordinate, F ∼ - x, so V(x) = kx2/2, for some k. The solutions are oscillatory, with angular frequency ω = 
. This model is called the simple harmonic oscillator.
2.1.2 The Least Action Principle
Every major theory can also be formulated by means of an idea known as the least action principle. Let us see how it works for the equations of Newtonian mechanics. Consider an arbitrary path of a particle x(t) and form the quantity
Here and below, the notation x may represent more than one coordinate. If x is used as a point in space-time, it will include the time coordinate, if that is not otherwise noted. Likewise, we omit component notation on most vectors. The notation should be clear from the context. The quantity S(x), which is known as the action, equals the kinetic energy minus the potential energy. One then considers which paths minimize this action. That is, we ask which paths x(t) have the property that, when they are perturbed by a small amount δx(t), the action is unchanged, to leading order. (So in fact we require only that the action is unchanged to first order, and not that it is actually minimized Solutions of saddle-point type are allowed.) The answer turns out to be precisely those paths that satisfy m + ∇V(x) = 0.2
For example, consider the simple harmonic oscillator in two dimensions. We can model x as a complex number and set V(x) = k|x|2. The action is then 
. Note that a phase rotation x → eiθ x leaves the action invariant, and is therefore a symmetry of the equations of motion.
Lesson. Physical solutions extremize the action.
The principle of least action applies to many other physical situations, as we shall see below. First, though, we describe another formulation of mechanics.
2.1.3 The Hamiltonian Formulation of Mechanics
HAMILTON’S [VI.37] formulation of the equations of motion also deserves mention. It leads to first-order equations. Let S be the action and define L by S = ∫ L dt, and consider the (typical) case where L is a function of coordinates x and their time derivatives 
. Then set p = dL/d, a function that can depend both on x and on . (In the example L = 
m2 - V(x) that we have already considered, we find that p = m, or = p/m.) Now let us consider the function H = p - L, which is called the HAMILTONIAN [III.35], and change variables from (x, ) to (x, p) so as to remove all mention of In the example, H works out to be
which is the total energy. For the simple harmonic oscillator, H = p2/2m + kx2/2.
The equations = ∂H/∂p and 
= -∂ H/∂x are the equations of motion in the Hamiltonian formulation; they can be shown to be equivalent to those obtained from the action principle. In the example, = p/m and = -∇V. Using the first equation to replace p by m in the second, we recover the equation m + ∇V(x) = 0. More generally, one can consider the time derivative of some quantity f(x, p) constructed from p and x and prove—using the chain rule and the equations of motion—that
The term in the middle is called the Poisson bracket of H and f, denoted {H, f}.
Lesson. The Hamiltonian controls time dependence through the Poisson bracket.
Notice that when we plug the coordinates x and p themselves into the bracket, we derive the identity
It is also possible to begin with the Hamiltonian viewpoint. One considers a space endowed with a bracket operation on functions, such that there are coordinate functions (not uniquely determined) obeying {x, p} -1. The mechanical model is defined by a function (x, p), which determines the dynamics.
2.1.4 Symmetry
A brief remark on symmetry is in order. NOETHER [VI.76] proved that in the action formulation of mechanics, a symmetry of the action results in a conserved quantity. The prototypical example is translational or rotational symmetry, where the potential of a particle is invariant under some direction of translation or rotation: the corresponding conserved quantity is then momentum or angular momentum. In the example above, V(x) = k|x|2/2 is independent of θ, the phase of x. The equation of motion determined by varying θ is d(m|x|2
)/dt = 0, so in this case it is the angular momentum m|x|2 that is conserved. In the Hamiltonian formulation, since a conserved quantity f (x, p) does not change with time, it must have zero Poisson bracket with the Hamiltonian: {H, f} = 0. In particular, the Hamiltonian itself is conserved.
2.1.5 Action Functions for Other Theories
Returning now to action principles, we shall see how different physical theories are described through different actions. In electricity and magnetism, MAXWELL’S EQUATIONS [IV.13 §1.1] can be formulated in the form δS = 0, where now the action S takes the form of an integral over space and time of the electric (E) and magnetic (B) fields. In the case where there are no sources, the action is written
where e is the electric charge of an electron. There is one important difference from the previous example, which is that the variations of the action must be taken with respect to the fundamental fields, and E and B are not fundamental as they are derived from the electromagnetic potential A = (ϕ, A) by the equations E = ∇ϕ - 
, B = ∇ × A. If you rewrite S in terms of A, vary A by δA, and set δS = 0, then you recover Maxwell’s equations from the least action principle.
It is clear that the electromagnetic action merely changes sign under the replacement E → B, B → -E, and therefore any solution δS = 0 remains a solution under the transformation. This is an example of an equivalence of a classical theory of physics. In fact, this symmetry extends to the case where there are sources (such as electrons) if we also interchange electric and magnetic sources. (No magnetic sources have been observed in the universe, but a theory with such objects still makes sense.)
Lesson. Physical equivalences act on fields and their sources.
Electricity and magnetism is a “field theory,” which means that the degrees of freedom involve functions that depend on position in space. Contrast this with Newtonian mechanics, where the spatial degrees of freedom are just the coordinates of the particle(s). However, there is not much conceptual distance between the two, as can be seen in the following toy model.
We will consider the simplest example: a scalar field, ϕ. That is, ϕ is just a function that takes numerical values. Now imagine that space has just one dimension, not three, and further that that dimension is a circle, which we can describe with an angular coordinate, θ. At any fixed point in time we can use FOURIER SERIES [III.27] to write the scalar field as ψ(θ) = Σncn exp(inθ), where the cn are the Fourier coefficients, and if we want the values of ψ to be real numbers then we must insist that c-n = 
. We can then think of ϕ(θ) not as a function but as an infinite-dimensional vector (c0, c1,. . .). The spatial dependence of ϕ is completely determined by the coefficients cn. If we now wish to consider time dependence, then all we have to do is use time-dependent components (c0 (t), C1 (t),. . .), which looks a lot like an infinite set of quantum-mechanical particles cn. Thus, the function ϕ has the Fourier expansion ϕ(θ, t) = Σn cn (t) exp(inθ).
The simplest action for a scalar field ϕ that allows wave-like solutions of the equations of motion serves as a natural analogue of equation (2):
where φ′ = ∂ϕ/∂θ. When we plug the Fourier expansion into the action and perform the θ integration, we get
Note that the term in brackets is just the action for a particle cn in a quadratic potential, as in section 2.1.2. We simply have an infinite number of harmonic oscillators (with the exception of the c0 degree of freedom, which corresponds to a free particle in no potential).
Lesson. Field theory is like point particle theory with an infinite number of particles. The particles correspond to the degrees of freedom of the field. When the action is just quadratic in the derivatives, the particles have an interpretation as simple harmonic oscillators.
Even GENERAL RELATIVITY [IV. 13] fits into this framework as a field theory. For a space-time M, the field is the RIEMANNIAN METRIC [I.3 §6.10] on space-time. The metric is what determines the lengths of paths between points—so a stretching of space-time, for example, is represented by a rescaled metric. The action is then constructed as the integral of the Riemannian curvature scalar 
over space-time: S = ∫M .3
2.2 Quantum Theory
Mirror symmetry is an equivalence of quantum theories, so we must develop an understanding of what a quantum theory is and what an equivalence looks like. There are two formulations of quantum mechanics: the operator formulation and Feynman’s path-integral formulation.
Both formulations are probabilistic, meaning that you cannot predict exactly what will be observed in a single measurement, but you can make precise predictions about what will be observed after multiple, repeated measurements in the same environment. For instance, your experimental apparatus may involve a beam of electrons hitting a screen and making a mark. The beam will contain millions of electrons, so the pattern of marks on the screen can be predicted with great accuracy. However, we cannot say what will happen to a single, given electron—all we can do is assign probabilities to the outcomes of various measurements. These probabilities are encoded in the so-called “wave function” Ψ of the particle.
2.2.1 Hamiltonian Formulation
In the operator formulation of quantum mechanics, the positions and momenta of classical mechanics (and any quantity formed from them) are converted into OPERATORS [III.50] acting On a HILBERT SPACE [III.37] according to the following rule: replace the Poisson bracket {· , ·} byi/
[· , ·], where [A, B] = AB-BA is the commutator bracket and is Planck’s constant. Thus, for example, we get from equation (1) the relation [x, p] = i. The state of a particle (or system) is now defined not as a set of values of x and p but as a vector Ψ in the Hilbert space. Once again, time evolution is determined by the Hamiltonian, H, but now H is an operator. The basic dynamical equation is
This is called the Schrödinger equation.
Lesson. To quantize a classical theory, replace ordinary degrees of freedom by operators on a vector space; replace Poisson brackets by commutator brackets.
In the case where we have a particle on the real line 
, the Hilbert space is the space of square-integrable functions L2(), so we write Ψ as Ψ(x). The commutation relation is obeyed if we think of x as the operator that sends the function Ψ(x) to the function xΨ(x). Now the relation [x, p] = i means that we should represent p as the operator -i(d/dx). The values of the classical quantity associated with an operator correspond to the EIGENVALUES [I.3 §4.3] of that operator, so for example a state with momentum p has the form Ψ ∼ exp(ipx/). Unfortunately, this is not squareintegrable on the real line, but it would become so if we identified x and x + 2πR, for some number (radius) R > 0. Topologically, this COMPACTIFIES [III.9] to a circle, but note that Ψ will be single-valued only if p = n/R, where n is an integer. Thus, momentum is “quantized” in units of /R.4 The integer label of the cn of equation (4) can therefore also be thought of as a momentum.
In the above example, is the degree of freedom of the classical coordinate x. In other examples, there is a copy of L2 () for each real degree of freedom, whether or not it represents a geometric location.
Another novelty is that position and momentum do not commute as operators in quantum mechanics, meaning they cannot be simultaneously diagonalized: you cannot specify the position and momentum simultaneously. This is a form of Heisenberg’s uncertainty principle (see OPERATOR ALGEBRAS [IV.15 §1.3]).
2.2.2 Symmetry
As the rules of quantization would suggest, a symmetry of a quantum theory is an operator A such that [H, A] = 0. That is, A commutes with the Hamiltonian, and therefore respects the dynamics.
2.2.3 Example: The Simple Harmonic Oscillator
We now discuss an example that will be useful later on for understanding quantum field theory and mirror symmetry: the simple harmonic oscillator in quantum mechanics. Suppose that the constants are chosen so that the Hamiltonian is given by H = x2 + p2. If one defines a = (x + ip)/
and a† = (x - ip)/, then one can show that a† raises the energy of a state by one units5 and a lowers the energy by one unit. Invoking the physical argument that there is a ground state Ψ0 of lowest energy, this state must obey aΨ0 = 0. One then finds that all states can be written in terms of the basis vectors Ψn = (a†)nΨ0 with energy n + . Note that Ψ0 has energy .6 The basis {Ψn} is called the occupation number basis, since the interpretation is that Ψn has n energy “quanta” above the ground state.
|
H(a†Ψ) = (Ha† - a†H + a†H)Ψ = ([H, a†] + a†H)Ψ |
|
= (a† + a†E)Ψ = (E + 1) (a†Ψ). |
We learn that a†Ψ has eigenvalue E + 1, so a† has “raised” the energy by one unit.
2.2.4 Path-Integral Formulation
Feynman’s path integral formulation of quantum mechanics builds on the idea of the least action principle. In this formulation, the probability of an experiment is calculated through an average over all paths of particles, and not just the ones which extremize the action. Each path x(t) is weighted by the factor exp(iS(x)/), where S(x) is the action of the path x(t) and is Planck’s constant, which is very small compared with macroscopic action scales. This average can be an imaginary number, but the probability of the process is the square of its absolute value.
Note that exp(iS/) = cos(S/) + i sin(S/), so if S changes appreciably when we vary x(t), then the real and imaginary parts will oscillate rapidly, since is small. Then, when we integrate over paths x(t), the positive and negative oscillations will roughly cancel. As a result, the main contributions to the weighted sum over paths will come from those paths for which S does not vary when the path does: the classical paths! However, if the variations are sufficiently small compared with then nonclassical paths can contribute appreciably. One typically separates the degrees of freedom into the classical trajectory piece and the quantum fluctuations near it. Then one can organize the path integral in a perturbation theory around the parameter .
We have not yet discussed the integrand of the path integral, and will not go into the details of this. The main point is that the theory makes a prediction about the likelihood of measuring a physical process. Each process determines a possible integrand. For example, from our discussion above we learn that the integrand for measuring the likelihood of a quantum-mechanical particle going from the point x0 at time t0 to the point x1 at time t1 gives nonzero weight—determined by the exponentiated action—to all paths that go from x0 to x1 as t goes from t0 to t1, and zero weight to all other paths.
It is illustrative to consider a toy model of a path integral on a “space-time” that consists of just a single point. Then the possible “paths” of a scalar field, say, are simply the values that the field can take at the point, so they are real numbers. The action is then an ordinary function S(x) on . For the purposes of this example, let us consider the case where iS/ = -x2 + λx3. The possible integrands are (sums of) powers of x, so the basic path integrals to perform are ∫ xk exp(- x2 + λx3) dx, which we denote by (xk). The value at λ = 0 is easily calculated.7 For small λ we expand eλx3 as 1 + λx3 + λ2x6/2 + · · ·, and evaluate each term by the same methods as for λ = 0. This is how we construct a welldefined perturbation theory, even when the integral is not calculable.
As we see from this example, path integrals are easiest when the action is only quadratic in the variables, just as we found in the operator formulation of quantum mechanics. The mathematical reason for this is that Gaussian integrals (exponentials of squares) can be done explicitly, while integrals involving exponentials of cubics or higher are difficult or impossible. For quadratic actions, the path integral can be evaluated exactly, but when cubic or higher terms appear, the perturbation series is necessary.
2.2.5 Quantum Field Theory
The generalization to field theories follows our earlier pattern. We think of quantum field theories, then, as being like quantum mechanics with infinite numbers of particles. In fact, the quantum field theories in which the fields Φ and their derivatives do not have more than quadratic terms in the action are easily understood in this way—we had a preview of this in equation (4). The Fourier components correspond to particles indexed by their momenta. Each one looks like a simple harmonic oscillator at some frequency, which will depend on the Fourier coefficient. The quantum Hilbert space is then a (tensor) product of lots of different “occupation number Hilbert spaces,” one for each Fourier component of each field. Since the occupation number basis is also an energy eigenbasis, these states have a simple time evolution under the Hamiltonian H. That is, if H = E on some state Ψ(t = 0), then that state evolves like
Ψ(t) = exp(iEt/)Ψ(0).
However, if the action includes terms that are cubic or higher, then things get interesting: particles can decay! This can be seen, for example, from the scalar field of equation (3) if we include a term ϕ3 in the action, and therefore also the Hamiltonian. If we write this using Fourier components, we get terms involving three oscillators, such as 
. To see this, recall that after we quantize the real field ϕ, the Fourier components cn act as harmonic oscillators, and we have written an for the associated creation and annihilation operators. Since the Hamiltonian governs time evolution according to equation (5), this means that over time one particle (the 7 mode) can decay into two others (the 3 and the 4). Such decay processes occur in real life, and it is a great triumph of quantum field theory that it can predict such events with astounding accuracy.
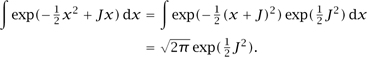
Now if we differentiate this answer with respect to J, and set J = 0, we get (x). Taking k derivatives gives (xk), and the theory is solved.
In fact, because the space of paths of fields is infinite dimensional, the path integral in quantum field theory is not usually defined in a mathematically rigorous way. However, the perturbation series for producing predictions can be defined just as for quantum mechanics, and this is how physicists make their predictions in practice. This perturbation series is organized in terms of Feynman diagrams (which are discussed in VERTEX OPERATOR ALGEBRAS [IV.17]). These diagrams, and the rules for computing them, completely solve the perturbation problem.
As in the example of quantum mechanics, different integrands of the path integral correspond to different predictions. If Φ is some function of the fields of some quantum field theory, we write 〈Φ〉 for the path integral with Φ as an integrand (as we did for 〈xk〉 in the previous section). We call such a term a “correlation function.” If Φ = ϕ1 (x1) · · · ϕn(xn), the answer will depend on the action of the theory, the fields ϕi, and the space-time points xi.
One might wonder if a symmetry of a classical theory always remains a symmetry of the same theory after quantization. The answer is sometimes no. Such a case is known as an “anomaly.” Roughly speaking, this is because the measure of integration of the path integral is not preserved under the symmetry, but this is a somewhat heuristic explanation because the path integral has no rigorous definition in general.
Returning to our cubic example, if the interaction term ϕ3 has a coefficient λ, so that it is λϕ3, then we organize the perturbation series as a power series in λ. In terms of paths, probabilities of decay processes can be evaluated by considering paths that split into two—like the letter Y—with each leg carrying the label of the appropriate particle.
2.2.6 String Theory
Feynman’s perturbation theory has an important generalization in string theory. String theory considers particles not as points but as loops. Instead of paths of particles through space-time, we get paths of loops, which look like two-dimensional surfaces. String theory amplitudes are computed by summing over all surfaces. These sums are organized in a perturbation series in powers of the so-called string coupling constant, λg. The power of λg in the perturbation series depends on the number of holes in the surface.
The surfaces are called worldsheets. At each point of the worldsheet, its location in space-time is determined by coordinates Xi. These coordinates themselves depend on the location on the worldsheet. In effect, we get an auxiliary theory: a field theory of coordinates on the two-dimensional surface! In string theory, even this two-dimensional field theory must be considered as a quantum field theory. The fields of the two-dimensional theory are maps from the surface to actual space-time. However, from the point of view of the worldsheet, the worldsheet itself is a two-dimensional space-time and the maps are fields on this space-time with values in some other (target) space.
Mirror symmetry was discovered as a result of the study of these quantum field theories on two-dimensional surfaces. Subsequently, the same phenomenon was discovered in the case where the strings were not closed loops but filaments with endpoints. Both cases play an important role below.
3 Equivalence in Physics
Mirror symmetry is a particular type of equivalence of quantum field theories. As we have seen, quantum field theories are rules for producing probabilities of physical processes. In the path-integral formulation, probabilities are computed from correlation functions of fields. According to Feynman, these correlation functions can be thought of as being averages over all paths of fields. Each path is weighted by exp(iS/), where S is the action of the path and is Planck’s constant. Let us denote the correlation function of some integrand Φ in theory A as 〈Φ〉A. Recall that Φ can depend on various fields ϕi and points of space-time xi, and the correlation function will depend on all these and the action of theory A.
Equivalence, then, is a map from all possible fields ϕi in a theory A to corresponding fields 
in a theory B such that
(For the moment, we deliberately neglect to notate the dependence on the points xi.) One special correlation function is 〈1〉, which we call the partition function and denote by Z. As the field 1 always gets mapped to 1, we derive the corollary that the partition functions must be equal: ZA = ZB.
Of course, this all has a description in the operator formulation of the quantum theory. Each state Ψ and each operator a in one theory must get mapped to a corresponding state 
and operator 
in the mirror theory, in such a way that corresponding operators map corresponding states to states which themselves correspond. Here one sees the sharp analogy with the slide rule and the operations of multiplication and addition of numbers.
Each theory is typically described through some mathematical model, so an equivalence implies a host of mathematical identities between quantities constructed from corresponding models.
The particular case of mirror symmetry refers to an equivalence of quantum field theories on a two-dimensional surface. The most typical example of mirror symmetry is the physical theory whose fields are maps 
from a two-dimensional RIEMANN SURFACE [III.79] Σ to some target space, M. Such a theory is called a sigma model. As we saw above, in string theory M plays the role of actual space-time, but for our purposes we can even consider the case where M is the real line , so that is an ordinary function. This case has already been studied in section 2.1.5. The action is given in equation (4). We can then write the partition function as
where [D] represents the measure of integration over all paths.8
One approach to evaluating the partition function Z is through a process known as Wick rotation. One first Euclideanizes the time coordinate by writing τ = it (this is the Wick rotation), which leads to an imaginary Euclidean action iSE. One then tries to evaluate the path integral in this framework, hoping that the answer will be HOLOMORPHIC [I.3 §5.6]. If it is, then one can use analytic continuation to work out the answer for ordinary time. The advantage is that the Euclidean exponential weighting becomes exp(-SE/), so the minima of SE receive the greatest weighting and the integral might converge. The nonconstant minima of the Euclidean action are called instantons. After Euclideanizing equation (4), the action becomes the “energy” SE of the map :
The energy of a map has a conformal symmetry, meaning that it is independent of local scale transformations on the Riemann surface, that is, transformations that can be locally approximated by a combination of rotations and dilations. Invariance under rescaling by a positive number λ can easily be seen: each of the two derivatives in |∇|2 decreases by a factor of λ, while the area element increases by λ2. Rotational invariance is clear from the form of |∇|2. The combination of the two, along with the fact that this argument did not depend on the derivatives of the scaling parameter λ, leads to the statement of local scale invariance.
The conformal symmetry of the action is an example of a classical symmetry of the action that is not necessarily maintained in the quantum theory. However, the quantum theory has no anomaly—meaning that the symmetry is preserved—if M is chosen to be a complex, CALABI–YAU MANIFOLD [III.6].
The Calabi–Yau condition can be thought of as a complex notion of orientation. Recall that for an oriented manifold one can continuously choose, on each patch, a basis for the tangent space such that, when we move from patch to patch, the determinant of the change-of-basis matrix is equal to one. The same is true on a Calabi–Yau manifold, but now we consider complex bases for the complex tangent spaces.
When the target manifold is a Calabi–Yau manifold, the instantons are complex analytic maps from the two-dimensional surface. Instantons are not “close” to the constant paths; their effects are therefore not accessible by perturbative methods such as Feynman diagrams. They are therefore “nonperturbative” phenomena. An example from quantum mechanics would be a particle in a double-well potential such as (x2 - 1)2. The zero-energy minima are the two constant (stationary) paths at x = ±1. An instanton path could go from x = -1 to x = + 1, or vice versa. Such trajectories occur and are known as “quantum tunneling.”
Lesson. Inaccessible by perturbation theory, instantonic effects are notoriously challenging to calculate.
3.1 Mirror Pairs
In the setting above, we considered maps from a two-dimensional surface Σ to a target (Calabi–Yau) space. Let us denote this quantum field theory by Q(M), which is shorthand for the collection of all fields and all possible correlation functions created from them. In this setup, we say that the Calabi–Yau manifolds M and W are “mirror pairs” if Q(M) is equivalent to Q(W). Through the magic of mirror symmetry, hard problems in Q(M) involving instantons can be answered in Q(W) by considering only the much simpler constant paths.
4 Mathematical Distillation
A physical theory contains a tremendous amount of information. For example, correlation functions can involve any number of fields, each evaluated at different points on the two-dimensional surface. This is typically too unwieldy a situation to approach mathematically. Instead, equipped with a symmetry of the theory called “supersymmetry,” a mathematical distillation can be performed. The distillation procedure is called topological twisting, and the resulting “topological field theory” has correlation functions that are independent of the positions of points. Because of this independence, the correlation functions are certain characteristic numbers associated with the underlying geometric setup. In fact, there are two types of twisting, typically called A and B, which capture different aspects of the manifold in question.
4.1 Complex and Symplectic Geometry
4.1.1 Complex Geometry
To get a feel for the geometric aspect captured by topological twisting, recall that we can construct the circle S1 from the real line by identifying the points θ and θ + 2π, and therefore also θ + 2πn, where n is any integer. What we have done is identified points related by a lattice of integer translations. We could choose the lattice to consist of multiples of some other real number r, but since any two such lattices differ only by an overall scaling of , we would effectively get the same space. In the complex plane , we can do the same thing with a two-dimensional lattice of translations generated by two complex numbers λ1 and λ2, as long as the quotient λ2/λ1 is not real. This space is called a torus and has the same topology as any two-dimensional surface with one hole. It has more structure, however, because it can be covered by regions described by a complex coordinate—with different regions related by complex analytic maps. The pairs (λ1, λ2) and (λ1, λ2 + λ1) generate the same lattice of translations, as do the pairs (λ1, λ2) and (λ2, - λ1). In fact, lattices related by a complex rescaling of 
are equivalent, so a better parametrization of the lattice is the ratio τ = λ2/λ1.
By redefining the direction of one of the λs, we can assume that the imaginary part of τ is positive, so τ takes values in the upper half of the complex plane. By the reasoning above, we note that τ and τ + 1, as well as -1/τ, all come from the same lattice. The number τ can also be thought of in the following way. The torus has two distinct loops, one generated by a straight path from z to z + λ1, and one generated by a straight path from z to z + λ2. Then λ1 and λ2 are both the result of the line integral of the complex differential dz over the loop. In fact, the loop did not even need to be straight to lead to this conclusion. The values of such integrals over subspaces without boundaries (the loops, here) are more generally called periods.
Although any two tori are topologically equivalent, one can show that there is no complex analytic map between two complex tori described by genuinely different values of τ. The parameter τ therefore determines the complex geometry of the space. Roughly speaking, we think of this parameter as describing the shape of the torus. (See MODULI SPACES [IV.8 §2.1] for a further discussion of this.)
The topological B-model depends only on the complex geometry of the target space M. That is, the theory depends, continuously, only on the parameter τ.
4.1.2 Symplectic Geometry
Another aspect of geometry is the size of the torus, which is described simply by an area element. Let us recall that, topologically, all tori look like 2 with points identified by the lattice of integer horizontal and vertical translations (but not necessarily in a way that would respect any complex geometry). The points of the torus can be thought of as the unit square with opposite sides glued together. An area element in 2 looks like ρ dx dy, which then determines the area ρ of the unit square. These notions of two-dimensional area generalize to two-dimensional subspaces in higher-dimensional spaces. The study of such structures is called SYMPLECTIC GEOMETRY [III.88], and so we call ρ the symplectic parameter.
The topological A-model depends only on the symplectic geometry of the target space M. That is, the theory depends, continuously, only on the parameter ρ.
4.2 Cohomological Theories
As you might imagine, the passage from an ordinary theory to a topological theory involves identifying many aspects of the physical theory that were previously distinct, such as different point values of a single field. Mathematically, a well-established method of producing topological aspects of a structure—and one that involves making identifications—is through a COHOMOLOGY THEORY [IV.6 §4]. Cohomology theories follow the pattern of having an operator δ obeying the equation δ ο δ = 0. We think of this equation as the statement image(δ) ⊂ ker (δ). The cohomology group H(δ) is formed as the quotient H(δ) = ker(δ)/image(δ), which means that we identify any two vectors u and v satisfying δu = δv = 0, so long as the difference u - v can be written as δw for some w. Then H(δ) is just the space of all such vectors, up to identifications.
The topological twisting of physical theories is similar. The operator δ is a physical operator acting on a Hilbert space of states. The presence of supersymmetry in our theories ensures that δ exists and squares to zero. The vector states of the topological theory are just the elements of H(δ), i.e., states in the original theory Ψ obeying δΨ = 0, up to identification. In many cases, these states can be identified with ground states.
It is crucial that supersymmetry is a symmetry that contains the complex translations of points on the two-dimensional surface. This means that the value of a field operator φ(z) at one point is identified with its value φ(z′) at another. In other words, the physics of the topological theory is independent of the positions of the operators! In the path-integral formulation, this means that the correlation functions are independent of the positions of the fields inserted into the integrand. What can they depend on, then? They depend on the particular field or combination of fields inserted, and they depend on the geometric parameter (such as ρ or τ) of the space M.
4.2.1 The A-Model aud the B-Model
Given a Calabi–Yau space, one can actually construct two operators, δA and δB, each of which squares to zero. There are therefore two distinct corresponding topological twistings and two distinct topological theories that can be constructed from a Calabi–Yau space.
If M and W are mirror Calabi–Yau pairs, you might wonder if the topological models constructed from them will still be equivalent theories. The answer is a most interesting form of yes: the resulting A-model of one Calabi–Yau manifold M is equivalent to the B-model of the mirror W, and vice versa! The complex and symplectic aspects of the theories get interchanged under mirror symmetry! In particular, a hard symplectic question of M might get mapped to an easy computation involving the complex geometry of W.
We emphasize here that the two manifolds may be completely topologically distinct. For example, the Euler characteristic of one is the negative of the other.
5 Basic Example: T-Duality
Although the circle is not complex, it provides a very illustrative entry into mirror symmetry that can be studied quite easily. We will find an equivalence between two theories constructed from circles. The equivalence will be very nontrivial, however, as states of very different kinds will be shown to correspond.
Consider the case where the two-dimensional surface is a cylinder, with spatial dimension a unit circle, and one dimension of time, and let us look at the sigma model (these were introduced in section 3). Suppose also that the target space is a circle of radius R, which we denote by 
. We think of as the real line, with two points identified if they differ by a multiple of 2πR. Maps from one circle to another can be classified by their winding number, an integer that tells you how many (net) times the image of a point goes around the second circle when the point goes once around the first. The map θ 
mRO from the circle to has winding number m. This allows us to write the field (θ) as a winding piece, mRθ, plus an honest Fourier series (no winding): 
. Here we have singled out the constant mode x = c0 of the Fourier series. We have expanded just the θ dependence in a series, so every continuous parameter (x and the cn) should be thought of as a function of time, as well.
The energy, or Hamiltonian, of such a map is computed as in section 2.1.3:
Comparing this with the harmonic oscillator Hamiltonian of section 2.1.3, we can see that each degree of freedom cn (t) plays the role of a (complex) quantum-mechanical particle in a simple harmonic oscillator potential. There is an occupation-mode basis for describing the quantum mechanics of each mode.9 The full Hilbert space of the quantum theory is the (tensor) product of each of these, plus parts involving the constant mode and winding number, which we now discuss. (Remember, each degree of freedom of the classical theory becomes a particle in the quantum field theory.)
The constant mode x has energy 2, and therefore has no associated potential (it can be anywhere on the circle). This mode represents a free quantum-mechanical particle on the circle. Recall that the momentum of the x particle is represented by the operator -i(d/dx). This operator has eigenfunctions eipx. The requirement that these eigenfunctions are invariant under the translation x → x + 2πR means that the eigenvalues of momentum are “quantized,” and have the form p = n/R.
In contrast to momentum, the integer winding number (m) is really a classical label for the possible maps from a circle to a circle. Although integral, it is clearly on a different footing from the integer n of momentum. Still, it is also an important label on the Hilbert space. For each m, we have a space of m-winding configurations which gets quantized to become the mth sector of the Hilbert space. Roughly, this sector
m comprises the functions of all the degrees of freedom of all the m-winding maps. We can consider the winding number as an operator by simply declaring that the states with winding number m have eigenvalue mR.
Ignoring the oscillator modes for the moment, the state of momentum n/R with winding m has energy (n/R)2 + (mR)2. In particular, the energy is unchanged if we make the simultaneous switches (m, n) ↔ (n, m) and R ↔ 1/R. Since the oscillator modes an, have energies that are independent of R, and since the modes are noninteracting particles, this symmetry can be extended to a full equivalence of the theories with targets and 
with momentum in one theory corresponding to winding number in the other.
In this example, the target space S1 is neither complex nor symplectic. As a result, we cannot construct the topological A- and B-models. Nevertheless, we have demonstrated the stronger statement that the two sigma models with target space and are equivalent. The theories are mirror pairs. In the special case of circles, mirror symmetry is referred to as T-duality. In fact, the entire phenomenon of mirror symmetry—even for noncircles—can be deduced from T-duality.
5.1 Tori
If we take the product of two circles 
× 
, we get a torus. We can think of the torus as a circle family of circles, since for each point in we have a circle . As we have seen in section 4.1.1, this space is complex—specifically, it is the complex plane quotiented by a lattice of translations. A particularly simple lattice is the one generated by the translations z → z + R1 and z → z + iR2. As discussed in section 4.1.1 above, the lattice is determined by the complex number τ = iR2/R1, equal to the ratio of integrals (“periods”) of the complex form dz over the two nontrivial loops of the torus.
The symplectic data is captured by the area element. Recall that we can choose coordinates x and y such that the identifications look like unit translations in each direction. Then the (normalized) area element of the torus with radii R1 and R2 is R1R2dxdy, which integrates to R1R2 on the unit square. Let us define the symplectic parameter ρ = iR1R2. We now perform T-duality for the first circle R1 → 1/R1. We see that under this substitution, the complex and symplectic parameters get interchanged:10
τ ↔ ρ.
Lessons. Mirror symmetry interchanges complex and symplectic parameters. Mirror symmetry is T-duality.
5.2 The General Case
The torus is the only compact one-dimensional Calabi–Yau space and is therefore the simplest one, but the discussion above is part of a more general picture. The Calabi–Yau condition ensures a unique complex volume element, or orientation (dz, above), whose “periods” determine, and in turn vary with, the complex parameters. Though the A- and B-models both turn out to be rather simple in the case of the torus, what is important in general is that the B-model is completely determined by how the periods of the complex volume element (which were λ1 and λ2 in section 4.1.1) change with the parameters of the theory (of which there was just one in section 4.1.1, namely τ). Again, the relation τ = λ2/λ1 is quite simple for the torus, but more complicated in general. In any case, this data gives all the information of the B-model. The reason for all of this is that the instantons of the B-model turn out to be just the constant maps. Each point of the target space determines a constant map, and as a result the B-model is reduced to (classical) complex geometry of the target space. This is determined by the periods.
This state of affairs is to be compared with the A-model. The A-model depends on the symplectic parameters ρ, i.e., the areas of two-dimensional surfaces inside the target space. In contrast to the B-model, however, the dependence on ρ is very complicated, in general. The reason for this is that the instantons of the A-model are area-minimizing surfaces inside the target space, and their enumeration is a notoriously challenging problem. (The problem is not terribly challenging for the torus, however.) Mathematically, the A-model instantons are described by the theory of Gromov-Witten invariants, the subject to which we now turn.
6 Mirror Symmetry and Gromov–Witten Theory
As we mentioned above, the B-model on W is explained entirely by the classical complex geometry of W. The only relevant maps for B-model computations are the constant ones, so the space of such maps is equal to W itself, and correlators reduce to (classical) integrals over W. In fact, one of the integrands to be integrated is the complex volume element. Let us call the parameter for all possible complex volume elements τ. B-model correlation functions are then determined by τ-dependent integrals over W. In particular, the partition function 
of the B-model on W depends on τ, so we write it as (τ).
The main point about topological twisting is that local variations of the fields are all identified, as they are related by the operator δ. In particular, varying the point on the worldsheet is a trivial operation in the topological theory. It turns out that, for the B-model on W, only the constant maps contributed, but for the A-model the situation is a bit more subtle. To give a feel for the geometry, consider again the winding of a map from a circle to a circle. Maps with different windings can never be deformed continuously into one another. The winding number is a measure of how the first circle “wraps” (or winds) around the target, according to the map. Because it is a discrete parameter it cannot change under continuous variations. Likewise, when M is a higher-dimensional space, the two-dimensional surface Σ can “wrap” around two-dimensional subspaces of M by different amounts. The parameters for wrapping are again discrete. A map can wrap Σ around the basic surfaces Ci in M by different integer amounts, ki. We say that k = ki labels the “class” of the map ϕ. (More precisely, (Σ) is a closed 2-cycle when Σ is compact, and k labels its homology class.) Different classes k contribute through different (Euclidean) actions Sk(ρ), which depend on the areas ρ and the class k but not on the continuous details of the map k. The partition function can have contributions from all classes. Different classes may contribute differently not only through the exponential weighting, but also in accordance with how many minimal surfaces they contain. (A good example of a minimal surface in three-dimensional space is a soap film If you fix the boundary with a wire, the soap film will seek to find the minimumarea surface with that boundary.) In our examples, the space M is actually complex; the minimal surfaces we speak of in Gromov-Witten theory are complex analytic maps from Σ. That is, if you have a complex coordinate for Σ, then the complex coordinates for the surfaces M can be written as complex analytic functions of Σ.
The difference between the A-model and the B-model comes from the fact that the topological model is constructed from an operator δ, which was guaranteed to exist by the presence of supersymmetry in our theories. For the different models, the relevant supersymmetry operators δA and δB are simply different. As we saw above, the maps relevant to the A-model are the instantons, or complex analytic maps from Σ to M. Roughly, then, A-model correlation functions on M, and in particular the partition function 
, are sums over classes k of surfaces in M and sums over instantons in each class, each one weighted by its instanton action exp(-Sk(ρ)). We have explicitly written the dependence on the parameter for the symplectic structure ρ. For Calabi–Yau manifolds, such maps should be discrete, and it is a conjecture, true in all known cases, that they are finite in number if we fix the class, k. All this data is packaged in a function of ρ, and based on what we have argued, the partition function must take the general form
The coefficients nk are called Gromov-Witten invariants.11
Putting things together, if (M, A) is mirror to (W, B), and if we can identify for each complex parameter τ for W a corresponding symplectic parameter ρ(τ) for M, then we have
The first equality means we should rewrite ρ in terms of τ, and the second says that the answer should be given by the corresponding B-model on W. Therefore, all of the information about complex analytic surfaces in M, which is encapsulated in the coefficients nk, is completely determined by the classical geometry of W!
This remarkable predictive power—the computation of an infinite number of difficult Gromov-Witten invariants through equations such as (6)—is what led to such intense interest in mirror symmetry at its inception.
7 Orbifolds and Nongeometric Phases
7.1 Nongeometric Theories
Mirror symmetry is about an equivalence of quantum field theories, and not every such field theory has the geometric content of a target space as in the sigma model. The structure involved in mirror symmetry—or at least its topological version—begins with a quantum theory with a supersymmetry algebra that allows for the passage to a topological theory. That is, there is a Hilbert space of states, a Hamiltonian operator, and a particular algebra of symmetries, i.e., operators that commute with the Hamiltonian. There are no dictates as to how one constructs such a setup, and the sigma model of maps to a target space is only one such way. Other methods abound. The geometric case is merely the one most suited for mathematicization (and exposition), which is why we have focused on the theory with a target space.
As an intermediate case—possibly geometric, possibly not—we will discuss the so-called orbifold theories.
7.2 Orbifolds
When space-time is a cylinder S1 × , with a circle S1 as its spatial dimension, there is a fascinating construction in quantum field theory known as an orbifold theory. This is defined as follows. Suppose there is a finite group G of symmetries (such as a reflection symmetry). That is, each group element acts as an operator on the Hilbert space, so if g ∈ G then it sends a state Ψ to a state gΨ. Then one defines a new theory by identifying states related by the symmetry. To construct the theory, let us first consider the ground state Ψ0 of the original theory. This is assumed to be invariant under the group: that is, 
Ψ0 = Ψ0 for all group elements, g.12 One then constructs the space 0 of all invariant states. This is known as the untwisted sector, and Ψ0 is the ground state of the untwisted sector. In the case where G is commutative, a twisted sector is then constructed for every group element g ∈ G.13 To construct the twisted sector, first think of the spatial dimension S1 as being an interval [0, 1] with endpoints 0 and 1 identified. Recall that the Hilbert space of states is constructed from (functions of) all the degrees of freedom of the possible configurations of fields. The twisted sector g corresponds to additional field configurations Φ that are related at the two ends by the action of g: so Φ(1) = gß(0). Such field configurations represent configurations on the circle S1 since left and right ends are related by the group, and therefore get identified. These additional configurations are thus part of the orbifold theory. One constructs a sector g of the Hilbert space by taking all such states Ψg that also obey the invariance condition hΨg = Ψg for all group elements h.
Orbifolds may be geometric, as they are in the case of the sigma model to a manifold X on which a discrete group G acts. For example, rotations act on the plane, and we can consider the four-element group generated by a right-angle rotation. The quotient of the plane by these rotations looks like a cone. As another example, the finite groups of symmetries of the platonic solids (tetrahedron, cube, etc.) act on the two-dimensional sphere by rotations. When we take X = S2 and G a platonic group, we get an interesting orbifold. In fact, if we simply take the space of orbits of the group G, it is topologically just a sphere again, but not a smooth one—it has cone points. These cone points would be troublesome in a quantum field theory, but the “stringy” orbifold is perfectly “smooth.”
The orbifold theory itself carries a symmetry. For example, if G is the commutative group with two elements, then there is an untwisted sector and a unique twisted sector. There is a symmetry corresponding to multiplication by 1 in the untwisted sector and by -1 in the twisted sector. This symmetry is not geometric. Orbifold theories with symmetries can often themselves be orbifolded in such a way as to recover the original theory. In fact, the theory and its orbifold are also often mirror pairs! Greene and Plesser used such a construction to create the first examples of mirror pairs. Furthermore, they used ways of ascribing geometric interpretations to some nongeometrically constructed theories so as to identify mirror Calabi–Yau spaces. To be precise, they took the space of all nonzero complex 5-vectors X = (X1, X2, X3, X4, X5) satisfying the equation
identifying X with λX for any nonzero complex number λ. (If X is a solution, then so is λX.) The equation actually defines a family of complex spaces, since τ ∈ is a parameter. The orbifold theory is defined from the finite group of phase transformations
where ω = e2πi/5 and 
is a multiple of 5. This space and its orbifold are actually the mirror pair about which Candelas et al. made their famous predictions.
8 Boundaries and Categories
The entire story of mirror symmetry becomes much richer when we allow the strings to have endpoints. Strings with ends are called “open strings,” while “closed strings” refers to loops. Mathematically, allowing ends corresponds to adding boundaries to the worldsheet surfaces. With this addition, we would like to perform the same topological twisting. To do so, we must first ensure that some supersymmetry condition persists when we put the boundary conditions on the fields. If we begin with a Calabi–Yau target manifold, we can ask to preserve the conditions that allow either the A-twisting or the B-twisting (but not both: the boundary condition will destroy some symmetry, much as pinning a rope will constrain its degrees of freedom). After the twist, the boundary topological theory will depend on symplectic or complex information, respectively.
For the A-model, the endpoints or boundaries must lie on a Lagrangian subspace. The Lagrangian condition constrains half the coordinates; for linear spaces it is like a restriction to the real part of a complex vector space. For the B-model the boundaries must lie on a complex space. Locally, a complex space looks like n and a complex subspace is described by complex analytic equations in the coordinates. A boundary condition that preserves supersymmetry and allows a chosen topological twisting is called a brane. (The terminology mimics the word “membrane,” but applies to any dimension.) In short, A-branes are Lagrangian; B-branes are complex.
To package all the information of the topological boundary theory, one appeals to the mathematical notion of a CATEGORY [III.8]. A category is a way of talking about structure: it consists of objects, and for any pair of objects there is a space of morphisms from one object to the other. Often the objects are mathematical structures of some kind and the morphisms from one object to another are the functions that preserve the relevant structure. For example, if the objects are (i) SETS [I.3 §2.1], (ii) TOPOLOGICAL SPACES [III.90], (iii) GROUPS [I.3 §2.1], (iv) VECTOR SPACES [I.3 §2.3], or (v) chain complexes, then the morphisms are, respectively, (1) MAPS [I.2 §2.2], (11) CONTINUOUS MAPS [III.90], (iii) HOMOMORPHISMS [I.3 §4.1], (iv) LINEAR MAPS [I.3 §4.2], or (v) chain maps. The morphism spaces between objects should be thought of as some kind of relational data. Morphisms themselves interact with one another, as they can be composed when the end object of one morphism is the start object of another. The composition is associative, so whether you compute abc as (ab)c or a(bc) does not matter. A useful image is a directed graph, which is a category with vertices as objects and paths between two vertices as morphisms. Composition is defined in this category by concatenating paths.
In the case of a two-dimensional field theory with boundary conditions, we construct a category whose objects are branes (i.e., boundary conditions). The morphisms between two branes α and β are the ground states αβ of the boundary field theory defined on the infinite strip [0, 1] × , where we put the boundary condition α on the left boundary {0} × and the condition β on the right boundary {1} × . Morphisms are composed by gluing boundaries together, and associativity is guaranteed by topological invariance.14
Mirror symmetry with boundary conditions then becomes the following statement: two manifolds M and W are mirror pairs if the brane category of the A-twisting of M is equivalent to the brane category of the B-twisting of W (and vice versa). The mathematical translation of this statement is called the homological mirror symmetry conjecture, due to Kontsevich. On the A-model side, the brane category is the so-called Fukaya category, and is governed by complex analytic maps from surfaces with boundaries, where the boundaries must be mapped to Lagrangian branes. On the B-model side, the branes form a category determined by complex subspaces, together with complex analytic VECTOR BUNDLES [IV.6§5] on them. A complex vector bundle associates a complex vector space to every point. For example, the complex circle {x2 + y2 = 1} in (2 has a complex tangent space at every point. “Complex analytic” means that this subspace of (2 changes in a complex analytic way. For the complex circle, the space of tangent vectors at (x, y) consists of all multiples of the vector (-y, x), an assignment which is clearly complex analytic. Physically, the bundles arise from allowing charges on the endpoints of strings.
Kontsevich’s conjecture asserts that these two categories of branes are equivalent. That statement is natural from the physics point of view, but by identifying the precise categories that correspond to the physical picture, this conjecture is a major contribution to the translation of mirror symmetry from physics into rigorous mathematics. The equivalence of categories means that not only is there a corresponding Lagrangian A-brane of M for every complex B-brane of W, but that the relationships, or morphisms, between branes are also in correspondence.
8.1 Example: Torus
Kontsevich’s conjecture can be proven and easily illustrated in the example of a 2-torus Think of the nowfamiliar symplectic two-torus as being the two-dimensional plane, with integer lattice translations identified. We take the torus to have area element A dx dy, so that the symplectic parameter is the imaginary number ρ = iA, as in section 4.1.2. Now consider straight lines on the plane. These will correspond to closed circles on the torus as long as they have rational slope: m = d/r, with d and r relatively prime integers. They are Lagrangian branes of the A-model boundary theory. The minimal-energy open strings connecting one line of slope m = d/r to another of slope m′ = d′/r′ are those that have zero length. They are therefore the points of intersection. It is an easy exercise to show that there are |dr′ - rd′| such points.
On the mirror side, we again have a torus, but with a complex parameter τ, and for the two tori to be mirror pairs, we should set τ = ρ. The objects of the B-model brane category are complex vector bundles. It is a theorem that the basic bundles are classified by their rank r and degree d, two integers.15 It is customary to organize these two numbers into what is known as a “slope,” m = d/r (the nomenclature preceded this application), and basic bundles must have d and r relatively prime.
We can now easily guess that under the mirror correspondence we have
slope ↔ slope.
This means that a Lagrangian brane of slope m on the torus with symplectic parameter ρ should correspond to a complex vector bundle with slope m in the mirror torus with complex parameter ρ. Now suppose we have the B-model version of our example above, so we take two vector bundles of slope m and m′. In fact, the minimum-energy open strings between two complex analytic bundles of slope m and m′ correspond to complex maps between the bundles, and the RIEMANNROCH FORMULA [V.31] counts this number as |dr′ - rd′|. This is the same result as for our A-model calculation above! Therefore, corresponding objects relate in a corresponding way. Beyond the morphism spaces, one checks finally that the compositions of corresponding morphisms correspond, just as for logarithms and slide rules. Doing so proves Kontsevich’s conjecture.
8.2 Definition and Conjecture
In fact, Kontsevich’s definition of mirror symmetry is really a conjecture stating that the boundary notion of mirror symmetry as an equivalence of categories is compatible with, and even implies, the traditional notion of mirror symmetry that relates Gromov–Witten theory and complex structures.
One way to show this is to try to reconstruct the Gromov–Witten invariants from the boundary theory. A heuristic, geometric approach to doing so involves looking at the diagonal boundary condition in two copies of a space. A disk mapping into two copies of a space is described by two maps of a disk into the space. Further, if the boundary condition is diagonal, this means that the maps have to agree on the boundary. What we have, then, is two disks inside a space which agree on the boundary. That is exactly what a sphere is: two disks (or cups) glued together! The disks are the two hemispheres, and they are glued along the equator. Now the minimal disks are instantons for the open string (with boundary), and by gluing them together along a common boundary, we have constructed a minimal sphere, or closed-string instanten. Thus the open string on this double theory should recover the closed string on the original theory.
A more algebraic approach sees the closed-string deformations as deformations of the category of branes. That is, a change in bulk (nonboundary) theory induces a change in boundary theory. But once equipped with a category, one can classify its deformations intrinsically. That is, if one views a category as a fancy algebra,16 then, as the deformations of an algebra are easily classified through a notion called Hochschild cohomology, the deformations of a category can be treated similarly. One arrives at the maxim that the closed string is the Hochschild cohomology of the open string. By computing the Hochschild cohomology of a brane category, one can, in principle, check this maxim, establish Kontsevich’s conjecture, and then prove the connection to traditional mirror symmetry and Gromov–Witten theory.
9 Unifying Themes
How does one find mirror pairs (M, W) What is the construction? Although mirror symmetry has spawned many results and proofs, these basic questions continue to vex.
On the one hand, Hori and Vafa have given a physics proof of mirror symmetry, which constructs mirror pairs but not through an evident mathematical channel. Of course, one can attempt to mathematicize the physical argument, but that does not seem to lead to insights into the construction—perhaps because path integrals and other methods of quantum field theory such as renormalization are not very well understood mathematically.
Batyrev has devised a procedure for constructing mirror pairs within the context of toric geometry. This method is a generalization, to a wide class of examples, of the original construction of Greene and Plesser. The recipe has been extremely successful in producing examples of every stripe. However, the underlying meaning behind the construction is unclear.
As for a geometric construction of mirror pairs, there is a physical argument that makes contact with mathematics, but it has not yet been made rigorous. The argument uses T-duality. Start with the B-model on M and consider a point P of M as a zero-dimensional complex subspace. Then the choice of point P on M is parametrized by M itself. By mirror symmetry, there should be a corresponding Lagrangian brane T on the mirror manifold W. Furthermore, the choices of T must equal the choices of P, i.e., the manifold M. Therefore, if we can find the brane T on W, we can parametrize the choices of T, and recover M. So we can find the mirror M of W from W itself.
This construction is geometric and has something to say about the structure of the Calabi–Yau spaces involved in mirror symmetry. Specifically, the choices of a Lagrangian brane always look like a family of tori. Therefore, M itself should look like a family of tori. Further, one can argue that by performing T-duality in families of tori (in a similar way to how one does it for a single torus), one arrives back at the mirror manifold, W. This is what we did for the torus, thought of as a circle family () of circles . When we T-dualized each member of the family, we found the mirror torus. So mirror symmetry is T-duality, and Calabi–Yau spaces of mirror symmetry should look like families of tori. This approach also relates to the homological mirror symmetry construction. Though promising, it remains mathematically elusive.
Various points of view on mirror symmetry are helpful for different applications. To date, no unified understanding of the phenomenon has been achieved. To some extent, we are still “feeling the elephant.”
10 Applications to Physics and Mathematics
As a computational tool in string theory, mirror symmetry is unparalleled in its power. When combined with other physical equivalences, its power is multiplied. For example, there are certain equivalences in physics that relate one type of string theory to another.
Without going into the details of string theory, we can get a flavor of its complexity by returning to mirror symmetry. Recall that the B-model was able to compute the difficult instantons on the A-model, yielding a great simplification of the two-dimensional quantum field theory on the worldsheet. But this whole quantum field theory was just an auxiliary tool for computing some Feynman diagram for the perturbation theory of the full string theory! Unfortunately, a satisfactory description of the full string theory path integral is, at the time of writing, way out of reach. String theory instanton effects are mostly unknown to us, unless a string equivalence or other argument can relate them to a perturbative effect in a different string theory. The perturbative string calculation in that other theory may then be performed by exploiting mirror symmetry. Tracing through chains of equivalences in such a manner, many different phenomena in string theory can ultimately be calculated via mirror symmetry.
In principle, one should be able to calculate all nonperturbative and perturbative aspects of a single theory by outsourcing the calculations to equivalent theories and exploiting mirror symmetry. The barriers to doing this at the time of writing are largely technological, not conceptual.
Beyond physics, the rich texture of mirror symmetry means that there is interesting mathematics to be discovered in the proper formulation of the problem. For example, defining the precise categories of branes in full generality remains a challenge.
Yet there are also direct applications to mathematical questions. We have already discussed how enumerative geometry has been revolutionized by mirror symmetry and the counting of instantons. Results in symplectic geometry have also been obtained. Occasionally, two objects may be proven to be equivalent as B-model branes. If the A-model mirrors can then be found, one has the result that the corresponding Lagrangian subspaces of the mirror symplectic space are also equivalent. Of course, to make such an argument, one must first prove Kontsevich’s version of mirror symmetry for the mirror pair considered. As a final recent example, Kapustin and Witten have found a relation of mirror symmetry to the geometric Langlands program in representation theory. This program, loosely stated, is a correspondence between objects associated with two-dimensional surfaces and Lie groups. From a surface Σ and a gauge group G, one constructs the space 
H of solutions to Hitchin’s equations. Central to that program are complex analytic objects on H that behave nicely under the action of an algebra of operations. The Langlands correspondence relates two sets of such objects: one easy to calculate and the other more difficult. In fact H is itself a family of tori, and the easy objects correspond to points. Mirror symmetry states that the points should turn into the tori under T-duality, so the hard objects should correspond to the tori themselves! It is an appealing proposition, and making it precise mathematics will be difficult—but the gauntlet has been thrown down.
The discovery that mirror symmetry relates to the geometric Langlands program has elicited great excitement among researchers and reveals yet another facet of this fascinating phenomenon.
The article “Physmatics” (which can be found online at www.claymath.org/library/senior_scholars/zaslow_physmatics.pdf) is a general discussion of the relationship between mathematics and physics, and may serve as a complement to this article. Readers with a university-level mathematics background who want to learn about mirror symmetry in more detail could try consulting the book Mirror Symmetry (Clay Mathematics Monographs, volume 1, edited by K. Hori and others (American Mathematical Society, Providence, RI, 2003)).
1. Acceleration is the second derivative of position with respect to time. We denote position by x, which is shorthand for a three-component position vector, and we denote time derivatives by dots, so acceleration is denoted by .
2. To see this, replace x by x+ δx in the action and keep only the linear terms in δx and its time derivative. For V the linear terms are (∇V)δx. One then has to integrate by parts to remove the time derivative of δx and isolate it as a factor in the integrand. The integral will be zero for arbitrary variations δx only when the term multiplying it vanishes. This gives the equation. Try it!
3. In 3-space, the paraboloid z = ax2 + by2 has curvature ab at the origin.
4. We shall occasionally choose our units to make equal to 1. For example, we could work in the fictitious time unit of “sgeconds,” one second equals sgeconds.
5. Here is the calculation: [a, a†] = 1 and H = a†a + . Further, [H, a†] = a† and [H, a] = -a. These equations have the following interpretation. Suppose Ψ is an eigenvector of H with eigenvalue (energy) E. Then HΨ = EΨ. Consider a†Ψ. One quickly finds that
6. It is instructive to write these equations in terms of the operators defined by x and p.
7. Consider
8. Warning: these expressions represent only the “bosonic” part of a theory with “supersymmetry,” meaning, in particular, that there are “fermionic” terms that complete the theory. We omit the fermionic completions for ease of notation and exposition.
9. Each 
is a raising operator, and similarly for the imaginary parts of the cn
10. The parameters τ and ρ can also have real parts, but we neglect the details for simplicity.
11. Though our discussion makes it seem as though the nk are integers, in fact they are only rational numbers. They can be expressed in terms of more basic integers, however. These integers are the ones referred to at the beginning of this article.
12. In the case where there are flat directions of a potential, as in a free particle on a circle (no potential at all), the ground state may be a superposition of classical values of the field. For the circle, the constant wave function Ψ = 1 is not associated with a single, classical location. It is still invariant under any group of rotations, however.
13. The twisted sectors are properly labeled by conjugacy classes, which are the same as group elements when G is commutative.
14. We speak of associativity of the topological states, which are themselves cohomology classes. At the “chain” level, before the topological twisting, there is no associativity. The notion of a category with morphisms that have a cohomology and compose only “up to cohomology” is called an A∞ category. One can also imagine a categorical definition that captures the structure of surfaces with handles and holes. Indeed, the proper mathematical framework for a complete understanding of mirror symmetry is still under construction.
15. A vector bundle assigns a vector space to each point of the torus. The rank is the dimension of that space. The degree is roughly a measure of the complexity of the bundle. For example, if we have a two-dimensional surface and consider the bundle that assigns to each point the tangent space at that point, the degree is equal to 2 - 2g, where g is the number of holes on the surface.
16. An algebra is a category with one object.