IV.9 Representation Theory
Ian Grojnowski
1 Introduction
It is a fundamental theme in mathematics that many objects, both mathematical and physical, have symmetries. The goal of GROUP [I.3 §2.1] theory in general, and representation theory in particular, is to study these symmetries. The difference between representation theory and general group theory is that in representation theory one restricts one’s attention to symmetries of VECTOR SPACES [I.3 §2.3]. I will attempt here to explain why this is sensible and how it influences our study of groups, causing us to focus on groups with certain nice structures involving conjugacy classes.
2 Why Vector Spaces?
The aim of representation theory is to understand how the internal structure of a group controls the way it acts externally as a collection of symmetries. In the other direction, it also studies what one can learn about a group’s internal structure by regarding it as a group of symmetries.
We begin our discussion by making more precise what we mean by “acts as a collection of symmetries.” The idea we are trying to capture is that if we are given a group G and an object X, then we can associate with each element g of G some symmetry of X, which we call ϕ(g). For this to be sensible, we need the composition of symmetries to work properly: that is, ϕ(g) ϕ(h) (the result of applying ϕ(h) and then ϕ(g)) should be the same symmetry as ϕ(gh). If X is a set, then a symmetry of X is a particular kind of PERMIJTATION [III.68] of its elements. Let us denote by Aut(X) the group of all permutations of X. Then an action of G on X is defined to be a homomorphism from G to Aut(X). If we are given such a homomorphism, then we say that G acts on X.
The image to have in mind is that G “does things” to X. This idea can often be expressed more conveniently and vividly by forgetting about ϕ in the notation: thus, instead of writing ϕ(g)(x) for the effect on x of the symmetry associated with g, we simply think of g itself as a permutation and write gx. However, sometimes we do need to talk about ϕ as well: for instance, we might wish to compare two different actions of G on X.
Here is an example. Take as our object X a square in the plane, centered at the origin, and let its vertices be A, B, C, and D (see figure 1). A square has eight symmetries: four rotations by multiples of 90° and four reflections. Let G be the group consisting of these eight symmetries; this group is often called D8, or the dihedral group of order 8. By definition, G acts on the square. But it also acts on the set of vertices of the square: for instance, the action of the reflection through the y-axis is to switch A with B and C with D. It might seem as though we have done very little here. After all, we defined G as a group of symmetries so it does not take much effort to associate a symmetry with each element of G. However, we did not define G as a group of permutations of the set {A, B, C, D}, so we have at least done something.
To make this point clearer, let us look at some other sets on which G acts, which will include any set that we can build sufficiently naturally from the square. For instance, G acts not only on the set of vertices {A, B, C, D}, but on the set of edges {AB, BC, CD, DA} and on the set of cross-diagonals {AC, BD} as well. Notice in the latter case that some of the elements of G act in the same way: for example, a clockwise rotation through 90° interchanges the two diagonals, as does a counterclockwise rotation through 90°. If all the elements of G act differently, then the action is called faithful.
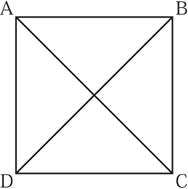
Figure 1 A square and its diagonals.
Notice that the operations on the square (“reflect through the y-axis,” “rotate through 90°,” and so on) can be applied to the whole Cartesian plane 
2. Therefore, 2 is another (and much larger) set on which G acts. To call 2 a set, though, is to forget the very interesting fact that the elements in 2 can be added together and multiplied by real numbers: in other words, 2 is a vector space. Furthermore, the action of G is well-behaved with respect to this extra structure. For instance, if g is one of our symmetries and v1 and v2 are two elements of 2, then g applied to the sum v1 + v2 yields the sum g(v1) + g(v2). Because of this, we say that G acts linearly on the vector space 2. When V is a vector space, we denote by GL(V) the set of invertible linear maps from V to V. If V is the vector space n, this group is the familiar group GLn() of invertible n × n matrices with real entries; similarly, when V = 
n it is the group of invertible matrices with complex entries.
Definition. A representation of a group G on a vector space V is a homomorphism from G to GL(V).
In other words, a group action is a way of regarding a group as a collection of permutations, while a representation is the special case where these permutations are invertible linear maps. One sometimes sees representations referred to, for emphasis, as linear representations. In the representation of D8 on 2 that we described above, the homomorphism from G to GL2() took the symmetry “clockwise rotation through 90°” to the matrix 
and the symmetry “reflection through the y-axis” to the matrix 
.
Given one representation of G, we can produce others using natural constructions from linear algebra. For example, if ρ is the representation of G on 2 described above, then its DETERMINANT [III.15] det ρ is a homomorphism from G to * (the group of nonzero real numbers under multiplication), since
det(ρ(gh)) = det(ρ(g)ρ(h)) = det(ρ(g)) det(ρ(h)),
by the multiplicative property of determinants. This makes det ρ a one-dimensional representation, since each nonzero real number t can be thought of as the element “multiply by t” of GL1(). If ρ is the representation of D8 just discussed, then under det ρ we find that rotations act as the identity and reflections act as multiplication by -1.
The definition of “representation” is formally very similar to the definition of “action,” and indeed, since every linear automorphism of V is a permutation on the set of vectors in V, the representations of G on V form a subset of the actions of G on V. But the set of representations is in general a much more interesting object. We see here an instance of a general principle: if a set comes equipped with some extra structure (as a vector space comes with the ability to add elements together), then it is a mistake not to make use of that structure; and the more structure the better.
In order to emphasize this point, and to place representations in a very favorable light, let us start by considering the general story of actions of groups on sets. Suppose, then, that G is a group that acts on a set X. For each x, the set of all elements of the form gx, as g ranges over G, is called the orbit of x. It is not hard to show that the orbits form a partition of X.
Example. Let G be the dihedral group D8 acting on the set X of ordered pairs of vertices of the square, of which there are sixteen. Then there are three orbits of G on X, namely {AA, BB, CC, DD}, {AB, BA, BC, CB, CD, DC, DA, AD}, and {AC, CA, BD, DB}.
An action of G on X is called transitive if there is just one orbit. In other words, it is transitive if for every x and y in X you can find an element g such that gx = y. When an action is not transitive, we can consider the action of G on each orbit separately, which effectively breaks up the action into a collection of transitive actions on disjoint sets. So in order to study all actions of G on sets it suffices to study transitive actions; you can think of actions as “molecules” and transitive actions as the “atoms” into which they can be decomposed. We shall see that this idea of decomposing into objects that cannot be further decomposed is fundamental to representation theory.
What are the possible transitive actions? A rich source of such actions comes from subgroups H of G. Given a subgroup H of G, a left coset of H is a set of the form {gh : h ∈ H}, which is commonly denoted by gH. An elementary result in group theory is that the left cosets form a partition of G (as do the right cosets, if you prefer them). There is an obvious action of G on the set of left cosets of H, which we denote by G/H: if g′ is an element of G, then it sends the coset gH to the coset (g′g)H.
It turns out that every transitive action is of this form! Given a transitive action of G on a set X, choose some x ∈ X and let Hx be the subgroup of G consisting of all elements h such that hx = x. (This set is called the stcibiiizer of x.)Then one can check that the action of G on X is the same1 as that of G on the left cosets of Hx. For example, the action of D8 on the first orbit above is isomorphic to the action on the left cosets of the two- element subgroup H generated by a reflection of the square through its diagonal. If we had made a different choice of x, for example the point x′ = gx, then the subgroup of G fixing x′ would just be gHxg-1. This is a so-called conjugate subgroup, and it gives a different description of the same orbit, this time as left cosets of gHxg-1.
It follows that there is a one-to-one correspondence between transitive actions of G and conjugacy classes of subgroups (that is, collections of subgroups conjugate to some given subgroup). If G acts on our original set X in a nontransitive way, then we can break X up into a union of orbits, each of which, as a result of this correspondence, is associated with a conjugacy class of subgroups. This gives us a convenient “bookkeeping” mechanism for describing the action of G on X: just keep track of how many times each conjugacy class of subgroups arises.
Exercise. Check that in the example earlier the three orbits correspond (respectively) to a two-element subgroup R generated by reflection through a diagonal, the trivial subgroup, and another copy of the group R.
This completely solves the problem of how groups act on sets. The internal structure that controls the action is the subgroup structure of G.
In a moment we will see the corresponding solution to the problem of how groups act on vector spaces. First, let us just stare at sets for a while and see why, though we have answered our question, we should not feel too happy about it.2
The problem is that the subgroup structure of a group is just horrible.
For example, any finite group of order n is a subgroup of the SYMMETRIC GROUP [III.68] Sn (this is “Cayley’s theorem,” which follows by considering the action of G on itself), so in order to list the conjugacy classes of subgroups of the symmetric group Sn one must understand all finite groups of size less than n.3 Or consider the cyclic group 
/n. The subgroups correspond to the divisors of n, a subtle property of n that makes the cyclic groups behave quite differently as n varies. If n is prime, then there are very few subgroups, while if n is a power of 2 there are quite a few. So number theory is involved even if all we want to do is understand the subgroup structure of a group as simple as a cyclic group.
With some relief we now turn our attention back to linear representations. We will see that, just as with actions on sets, one can decompose representations into “atomic” ones. But, by contrast with the case of sets, these atomic representations (called “irreducible” representations, or sometimes simply “irreducibles”) turn out to exhibit quite beautiful regularities.
The nice properties of representation theory come largely from the following fact. While elements of the symmetric group Sn can be multiplied together, elements of GL(V), being matrices, can be added as well as multiplied. (But beware: the sum of two elements of GL(V) is not necessarily an element of GL(V), because it may not be invertible. It is, however, an element of the endomorphism algebra End(V). When V = n, End(V) is just the familiar algebra of all n × n matrices with complex entries, both invertible and not.)
To see the difference it makes to be able to add, consider the cyclic group G = /n. For each ω ∈ with ωn = 1, we get a representation χω of G on by associating the element r ∈ /n with multiplication by ωr, which we think of as a linear map from the one-dimensional space to itself. This gives us n different one-dimensional representations, one for each nth root of unity, and it turns out that there are no others. Moreover, if ρ : G → GL(V) is any representation of /n, then we can write it as a direct sum of these representations by imitating the formula for finding the Fourier mode of a function. Using the representation ρ, we associate with each r in /n a linear map ρ(r). Now let us define a linear map pω : V → V by the formula
Then pω is an element of End(V), and one can check that it is actually a PROJECTION [III.50 §3.5] onto a subspace Vω of V. In fact, this subspace is an EIGENSPACE [I.3 §4.3]: it consists of all vectors v such that ρ(l)v = ωv, which implies, since ρ is a representation, that ρ(r)v = ωrv. The projection pω should be thought of as the analogue of the nth FOURIER COEFFICIENT [III.27] an(f) of a function f(θ) on the circle; note the formal similarity of the above formula to the Fourier expansion formula an(f) = ∫ e-2πinθ f(θ) dθ.
Now the interesting thing about the Fourier series of f is that, under favorable circumstances, it adds up to f itself: that is, it decomposes f into TRIGONOMETRIC FUNCTIONS [III.92]. Similarly, what is interesting about the subspaces Vω is that we can use them to decompose the representation ρ. The composition of any two distinct projections pω is 0, from which it can be shown that
We can write each subspace Vω as a sum of one- dimensional spaces, which are copies of , and the restriction of ρ to any one of these is just the simple representation χω defined earlier. Thus, ρ has been decomposed as a combination of very simple “atoms” χω.4
This ability to add matrices has a very useful consequence. Let a finite group G act on a complex vector space V. A subspace W of V is called G-invariant if gW = W for every g ∈ G. Let W be a G-invariant subspace, and let U be a complementary subspace (that is, one such that every element v of V can be written in exactly one way as w + u with w ∈ W and u ∈ U). Let ϕ be an arbitrary projection onto U. Then it is a simple exercise to show that the linear map 1/|G|Σg∈G g ϕ is also a projection onto a complementary subspace, but with the added advantage that it is G-invariant. This latter fact follows because applying an element g′ to the sum just rearranges its terms.
The reason this is so useful is that it allows us to decompose an arbitrary representation into a direct sum of irreducible representations, which are representations without a G-invariant subspace. Indeed, if ρ is not irreducible, then there is a G-invariant subspace W. By the above remark, we can write G = W ⊕ W′ with W′ also G-invariant. If either W or W′ has a further G-invariant subspace, then we can decompose it further, and so on. We have just seen this done for the cyclic group: in that case the irreducible representations were the one-dimensional representations χω.
The irreducible representations are the basic building blocks of arbitrary complex representations, just as the basic building blocks for actions on sets are the transitive actions. It raises the question of what the irreducible representations are, a question that has been answered for many important examples, but which is not yet solvable by any general procedure.
To return to the difference between actions and representations, another important observation is that any action of a group G on a finite set X can be linearized in the following sense. If X has n elements, then we can look at the HILBERT SPACE [III.3 7] L2(X) Of all complex-valued functions defined on X. This has a natural basis given by the “delta functions” δx, which send x to 1 and all other elements of X to 0. Now we can turn the action of G on X into an action of G on the basis in an obvious way: we just define g δx, to be δgx. We can extend this definition by linearity, since an arbitrary function f is a linear combination of the basis functions δx. This gives us an action of G on L2(X), which can be defined by a simple formula: if f is a function in L2(X), then gf is the function defined by (g f)(x) = f (g-1 x). Equivalently, g f does to gx what f does to x. Thus, an action on sets can be thought of as an assignment of a very special matrix to every group element, namely a matrix with only Os and is and precisely one 1 in each row and each column. (Such matrices are called permutation matrices.) By contrast, a general representation assigns an arbitrary invertible matrix.
Now, even when X itself is a single orbit under the action of G, the above representation on L2(X) can break up into pieces. For an extreme example of this phenomenon, consider the action of /n on itself by multiplication. We have just seen that, by means of the “Fourier expansion” above, this breaks up into a sum of n one-dimensional representations.
Let us now consider the action of an arbitrary group G on itself by multiplication, or, to be more precise, left multiplication. That is, we shall associate with each element g the permutation of G that takes each h in G to gh. This action is obviously transitive. As an action on a set it cannot be decomposed any further. But when we linearize this action to a representation of G on the vector space L2(G), we have much greater flexibility to decompose the action. It turns out that, not only does it break up into a direct sum of many irreducible representations, but every irreducible representation ρ of G occurs as one of the summands in this direct sum, and the number of times that ρ appears is equal to the dimension of the subspace on which it acts.
The representation we have just discussed is called the left regular representation of G. The fact that every irreducible representation occurs in it so regularly makes it extremely useful. Notice that it is easier to decompose representations on complex vector spaces than on real vector spaces, since every automorphism of a complex vector space has an eigenvector. So it is simplest to begin by studying complex representations.
The time has now come to state the fundamental theorem about complex representations of finite groups. This theorem tells us how many irreducible representations there are for a finite group, and, more colorfully, that representation theory is a “non-Abelian analogue of Fourier decomposition.”
Let ρ : G → End(V) be a representation of G. The character χρ of ρ is defined to be its trace: that is, χρ is a function from G to and χρ(g) = tr(ρ(g)) for each g in G. Since tr(AB) = tr(BA) for any two matrices A and B, we have χρ(hgh-1) = χρ(g). Therefore, χV is very far from an arbitrary function on G: it is a function that is constant on each conjugacy class. Let KG denote the vector space of all complex-valued functions on G with this property; it is called the representation ring of G.
The characters of the irreducible representations of a group form a very important set of data about the group, which it is natural to organize into a matrix. The columns are indexed by the conjugacy classes, the rows by the irreducible representations, and each entry is the value of the character of the given representation at the given conjugacy class. This array is called the character table of the group, and it contains all the important information about representations of the group: it is our periodic table. The basic theorem of the subject is that this array is a square.
Theorem (the character table is square). Let G be a finite group. Then the characters of the irreducible representations form an Orthonorma1 basis of KG.
When we say that the basis of characters is orthonormal we mean that the Hermitian inner product defined by
is 1 when χ = ψ and 0 otherwise. The fact that it is a basis implies in particular that there are exactly as many irreducible representations as there are conjugacy classes in G, and the map from isomorphism classes of representations to KG that sends each ρ to its character is an injection. That is, an arbitrary representation is determined up to isomorphism by its character.
The internal structure of a group G that controls how it can act on vector spaces is the structure of conjugacy classes of elements of G. This is a much gentler structure than the set of all conjugacy classes of subgroups of G. For example, in the symmetric group Sn two permutations belong to the same conjugacy class if and only if they have the same cycle type. Therefore, in that group there is a bijection between conjugacy classes and partitions of n.5
Furthermore, whereas it is completely unclear how to count subgroups, conjugacy classes are much easier to handle. For instance, since they partition the group, we have the formula |G| = Σc a conjugacy class |C|. On the representation side, there is a similar formula, which arises from the decomposition of the regular representation L2(G) into irreducibles: |G| = ΣV irreducibile(dim V)2. It is inconceivable that there might be a similarly simple formula for sums over all subgroups of a group.
We have reduced the problem of understanding the general structure of the representations of a finite group G to the problem of determining the character table of G. When G = /n, our description of the n irreducible representations above implies that all the entries of this matrix are roots of unity. Here are the character tables for D8 (on the left), the group of symmetries of the square, and, just for contrast, for the group /3 (on the right):
where z = exp(2πi/3).
The obvious question—Where did the first table come from?—indicates the main problem with the theorem: though it tells us the shape of the character table, it leaves us no closer to understanding what the actual character values are. We know how many representations there are, but not what they are, or even what their dimensions are. We do not have a general method for constructing them, a kind of “non-Abelian Fourier transform.” This is the central problem of representation theory.
Let us see how this problem can be solved for the group D8. Over the course of this article, we have already encountered three irreducible representations of this group. The first is the “trivial” one-dimensional representation: the homomorphism ρ : D8 → GL1 that takes every element of D8 to the identity. The second is the two-dimensional representation we wrote down in the first section, where each element of D8 acts on 2 in the obvious way. The determinant of this representation is a one-dimensional representation that is not trivial: it sends the rotations to 1 and the reflections to -1. So we have constructed three rows of the character table above. There are five conjugacy classes in D8 (trivial, reflection through axis, reflection through diagonal, 90° rotation, 180° rotation), so we know that there are just two more rows.
The equality |G| = 8 = 22 + 1 + 1 + (dim V4)2 + (dim V5)2 implies that these missing representations are one dimensional. One way of getting the missing character values is to use orthogonality of characters.
A slightly (but only slightly) less ad hoc way is to decompose L2(X) for small X. For example when X is the pair of diagonals {AC, BD}, we have L2(X) = V4 ⊕ , where is the trivial representation.
We are now going to start pointing the way toward some more modern topics in representation theory. Of necessity, we will use language from fairly advanced mathematics: the reader who is familiar with only some of this language should consider browsing the remaining sections, since different discussions have different prerequisites.
In general, a good, but not systematic, way of finding representations is to find objects on which G acts, and “linearize” the action. We have seen one example of this: when G acts on a set X we can consider the linearized action on L2(X). Recall that the irreducible G-sets are all of the form G/H, for H some subgroup of G. As well as looking at L2(G/H), we can consider, for every representation W of H, the vector space L2(G/H, W) = {f : G → W | f(gh) = h-1 f(g), g ∈ G, h ∈ H}; in geometric language, for those who prefer it, this is the space of sections of the associated W-bundle on G/H. This representation of G is called the induced representation of W from H to G.
Other linearizations are also important. For example, if G acts continuously on a topological space X, we can consider how it acts on homology classes and hence on the HOMOLOGY GROUPS [IV.6 §4] of X.6 The simplest case of this is the map z → 
of the circle S1. Since this map squares to the identity map, it gives us an action of /2 on S1, which becomes a representation of /2 on H1(S1) = (which represents the identity as multiplication by 1 and the other element of /2 as multiplication by -1).
Methods like these have been used to determine the character tables of all finite SIMPLE GROUPS [I.3 §3.3],but they still fall short of a uniform description valid for all groups.
There are many arithmetic properties of the character table that hint at properties of the desired non- Abelian Fourier transform. For example, the size of a conjugacy class divides the order of the group, and in fact the dimension of a representation also divides the order of the group. Pursuing this thought leads to an examination of the values of the characters mod ρ, relating them to the so-called p-local subgroups. These are groups of the form N(Q)/Q, where Q is a subgroup of G, the number of elements of Q is a power of p, and N(Q) is the normalizer of Q (defined to be the largest subgroup of G that contains Q as a normal subgroup). When the so-called “p-Sylow subgroup” of G is Abelian, beautiful conjectures of Broué give us an essentially complete picture of the representations of G. But in general these questions are at the center of a great deal of contemporary research.
3 Fourier Analysis
We have justified the study of group actions on vector spaces by explaining that the theory of representations has a nice structure that is not present in the theory of group actions on sets. A more historically based account would start by saying that spaces of functions very often come with natural actions of some group G, and many problems of traditional interest can be related to the decomposition of these representations of G.
In this section we will concentrate on the case where G is a compact LIE GROUP [III.48 §1]. We will see that in this case many of the nice features of the representation theory of finite groups persist.
The prototypical example is the space L2(S1) of square-integrable functions on the circle S1. We can think of the circle as the unit circle in , and thereby identify it with the group of rotations of the circle (since multiplication by eiθ rotates the circle by θ). This action linearizes to an action on L2(S1): if f is a square-integrable function defined on S1 and w belongs to the circle, then (w · f)(z) is defined to be f(w-1 z). That is, w · f does to wz what f does to z.
Classical Fourier analysis expands functions in the space L2(S1) in terms of a basis of trigonometric functions: the functions zn for n ∈ . (These look more “trigonometric” if one writes eiθ for z and einθ for zn.) If we fix w and write ϕn(z) = zn, then (w · ϕn)(z) = ϕn(w-1 z) = w-n ϕn(z). In particular, w · ϕn is a multiple of ϕn for each w, so the one-dimensional subspace generated by ϕn is invariant under the action of S1. In fact, every irreducible representation of S1 is of this form, as long as we restrict attention to continuous representations.
Now let us consider an innocuous-looking generalization of the above situation: we shall replace 1 by n and try to understand L2(Sn), the space of complex-valued square-integrable functions on the n-sphere Sn. The n-sphere is acted on by the group of rotations SO(n + 1). As usual, this can be converted into a representation of SO(n + 1) on the space L2(Sn), which we would like to decompose into irreducible representations; equivalently, we would like to decompose L2(Sn) into a direct sum of minimal SO(n + 1)-invariant subspaces.
This turns out to be possible, and the proof is very similar to the proof for finite groups. In particular, a compact group such as SO(n + 1) has a natural PROBABILITY MEASURE [III.71 §2] on it (called Haar measure) in terms of which we can define averages. Roughly speaking, the only difference between the proof for SO(n + 1) and the proof in the finite case is that we have to replace a few sums by integrals.
The general result that one can prove by this method is the following. If G is a compact group that acts continuously on a compact space X (in the sense that each permutation ϕ(g) of X is continuous, and also that ϕ(g) varies continuously with g), then L2(X) splits up into an orthogonal direct sum of finite-dimensional minimal G-invariant subspaces; equivalently, the linearized action of G on L2(X) splits up into an orthogonal direct sum of irreducible representations, all of which are finite dimensional. The problem of finding a Hilbert space basis of L2(X) then splits into two subproblems: we must first determine the irreducible representations of G, a problem which is independent of X, and then determine how many times each of these irreducible representations occurs in L2(X).
When G = S1 (which we identified with SO(2)) and X = S1 as well, we saw that these irreducible representations were one dimensional. Now let us look at the action of the compact group SO(3) on S2. It can be shown that the action of G on L2 (S2) commutes with the Laplacian, the differential operator Δ on L2(S2) defined by
That is, g(Δf) = Δ(gf) for any g ∈ G and any (sufficiently smooth) function f. In particular, if f is an eigenfunction for the Laplacian (which means that Δf = λf for some λ ∈ ), then for each g ∈ SO(3) we have
Δgf = gΔf = gλf = λgf,
so gf is also an eigenfunction for Δ. Therefore, the space Vλ of all eigenvectors for the Laplacian with eigenvalue λ is G-invariant. In fact, it turns out that if Vλ is nonzero then the action of G on Vλ is an irreducible representation. Furthermore, each irreducible representation of SO(3) arises exactly once in this way. More precisely, we have a Hilbert space direct sum,
and each eigenspace V2n(2n+2) has dimension 2n + 1. Note that this is a case where the set of eigenvalues is discrete. (These eigenspaces are discussed further in SPHERICAL HARMONICS [III.87].)
The nice feature that each irreducible representation appears at most once is rather special to the example L2 (Sn). (For an example where this does not happen, recall that with the regular representation L2(G) of a finite group G each irreducible representation ρ occurs dim ρ times in L2 (G).) However, other features are more generic: for example, when a compact Lie group acts differentiably on a space X, then the sum of all the G-invariant subspaces of L2 (X) corresponding to a particular representation is always equal to the set of common eigenvectors of some family of commuting differential operators. (In the example above, there was just one operator, the Laplacian.)
Interesting SPECIAL FUNCTIONS [III.85], such as solutions of certain differential equations, often admit representation-theoretic meaning, for example as matrix coefficients. Their properties can then easily be deduced from general results in functional analysis and representation theory rather than from any calculation. Hypergeometric equations, Bessel equations, and many integrable systems arise in this way.
There is more to say about the similarities between the representation theory of compact groups and that of finite groups. Given a compact group G and an irreducible representation ρ of G, we can again take its trace (since it is finite dimensional) and thereby define its character. χρ. Just as before, χρ is constant on each conjugacy class. Finally, “the character table is square,” in the sense that the characters of the irreducible representations form an orthonorma1 basis of the Hilbert space of all square-integrable functions that are conjugation invariant in this sense. (Now, though, the “square matrix” is infinite) When G = S1 this is the Fourier theorem; when G is finite this is the theorem of section 2.
4 Noncompact Groups, Groups in Characteristic p, and Lie Algebras
The “character table is square” theorem focuses our attention on groups with nice conjugacy-class structure. What happens when we take such a group but relax the requirement that it be compact?
A paradigmatic noncompact group is the real numbers . Like S1, acts on itself in an obvious way (the real number t is associated with the translation s 
s + t), so let us linearize that action in the usual way and look for a decomposition of L2 () into -invariant subspaces.
In this situation we have a continuous family of irreducible one-dimensional representations: for each real number λ we can define the function χλ by χλ (x) = e2Πiλx These functions are not square integrable, but despite this difficulty classical Fourier analysis tells us that we can write an L2-function in terms of them. However, since the Fourier modes now vary in a continuous family, we can no longer decompose a function as a sum: rather we must use an integral. First, we define the Fourier transform 
of f by the formula (λ) = ∫ f (x)e2πiλx dx. The desired decomposition of f is then f (x) = ∫ (λ)e–2πiλx dλ. This, the Fourier inversion formula, tells us that f is a weighted integral of the functions χλ. We can also think of it as something like a decomposition of L2() as a “direct integral” (rather than direct sum) of the one-dimensional subspaces generated by the functions χλ. However, we must treat this picture with due caution since the functions χλ do not belong to L2 ().
This example indicates what we should expect in general. If X is a space with a measure and G acts continuously on it in a way that preserves the measures of subsets of X (as translations did with subsets of ), then the action of G on X gives rise to a measure μX defined on the set of all irreducible representations, and L2(X) can be decomposed as the integral over all irreducible representations with respect to this measure. A theorem that explicitly describes such a decomposition is called a Plancherel theorem for X.
For a more complicated but more typical example, let us look at the action of SL2() (the group of real 2 × 2 matrices with determinant 1) on 2 and see how to decompose L2(2). As we did when we looked at functions defined on S2, we shall make use of a differential operator. This involves the small technicality that we should look at smooth functions, and we do not ask for them to be defined at the origin. The appropriate differential operator this time turns out to be the Euler vector field x(∂/∂x + y(∂/∂y). It is not hard to check that if f satisfies the condition f (tx, ty) = ts f (x,y) for every x,y, and t > 0, then f is an eigenfunction of this operator with eigenvalue s, and indeed all functions in the eigenspace with this eigenvalue, which we shall denote by Ws, are of this form. We can also split Ws up as 
⊕ 
where and consist of the even and odd functions in Ws, respectively.
The easiest way of analyzing the structure of Ws is to compute the action of the LIE ALGEBRA [III.48 §2] 
2. For those readers unfamiliar with Lie algebras, we will say only that the Lie algebra of a Lie group G keeps track of the action of elements of G that are “infinitesimally close to the identity,” and that in this case the Lie algebra 2 can be identified with the space of 2 × 2 matrices of trace 0, with 
acting as the differential operator (–ax – by) (∂/∂x) + (–cx + ay) (∂/∂y).
Every element of Ws is a function on 2. If we restrict these functions to the unit circle, then we obtain a map from Ws to the space of smooth functions defined on S1, which turns out to be an isomorphism. We already know that this space has a basis of Fourier modes zm, which we can now think of as (x + iy)m, defined when x2 + y2 = 1. There is a unique extension of this from a function defined on S1 to a function in Ws, namely the function wm (x,y) = (x + iy)m (x2 + y2)(s–m)/2. One can then check the following actions of simple matrices on these functions (to do so, recall the association of the matrices with differential operators given in the previous paragraph,
It follows that if s is not an integer, then from any function wm in we can produce all the others using the action of SL2(). Therefore, SL2() acts irreducibly on Similarly, it acts irreducibly on We have therefore encountered a significant difference between this and the finite/compact case: when G is not compact, irreducible representations of G can be infinite dimensional.
Looking more closely at the formulas for Ws when s ∈ , we see more disturbing differences. In order to understand these, let us distinguish carefully between representations that are reducible and representations that are decomposable. The former are representations that have nontrivial G-invariant subspaces, whereas the latter are representations where one can decompose the space on which G acts into a direct sum of G-invariant subspaces. Decomposable representations are obviously reducible. In the finite/compact case, we used an averaging process to show that reducible representations are decomposable. Now we do not have a natural probability measure to use for the averaging, and it turns out that there can be reducible representations that are not decomposable.
Indeed, if s is a nonnegative integer, then the subspaces and and give us an example of this phenomenon. They are indecomposable (in fact, this is true even when s is a negative integer not equal to – 1) but they contain an invariant subspace of dimension s + 1. Thus, we cannot write the representation as a direct sum of irreducible representations. (One can do something a little bit weaker, however: if we quotient out by the (s + 1)-dimensional subspace, then the quotient representation can be decomposed.)
It is important to understand that in order to produce these indecomposable but reducible representations we worked not in the space L2(2) but in the space of smooth functions on 2 with the origin removed. For instance, the functions wm above are not square integrable. If we look just at representations of G that act on subspaces of L2 (X), then we can split them up into a direct sum of irreducibles: given a G-invariant subspace, its orthogonal complement is also G-invariant. It might therefore seem best to ignore the other, rather subtle representations and just look at these ones. But it turns out to be easier to study all representations and only later ask which ones occur inside L2(X). For SL2(), the representations we have just constructed (which were subquotients of 
) exhaust all the irreducible representations,7 and there is a Plancherel formula for L2(2) that tells us which ones appear in L2 (2) and with what multiplicity:
To summarize: if G is not compact, then we can no longer take averages over G. This has various consequences:
Representations occur in continuous families The decomposition of L2(X) takes the form of a direct integral, not a direct sum.
Representations do not split up into a direct sum of irreducibles. Even when a representation admits a finite composition series, as with the action of SL2 () on , it need not split up into a direct sum. So to describe all representations we need to do more than just describe the irreducibles—we also need to describe the glue that holds them together.
So far, the theory of representations of a noncompact group G seems to have none of the pleasant features of the compact case. But one thing does survive: there is still an analogue of the theorem that the character table is square. Indeed, we can still define characters in terms of the traces of group elements. But now we must be careful, since the irreducible representation may be on an infinite-dimensional vector space, so that its trace cannot be defined so easily. In fact, characters are not functions on G, but only DISTRIBUTIONS [III.18]. The character of a representation determines the semisimplification of a representation ρ: that is, it tells us which irreducible representations are part of ρ, but not how they are glued together.8
These phenomena were discovered by Harish-Chandra in the 1950s in an extraordinary series of works that completely described the representation theory of Lie groups such as the ones we have discussed (the precise condition is that they should be real and reductive—a concept that will be explained later in this article) and the generalizations of classical theorems of Fourier analysis to this setting.9
Independently and slightly earlier, Brauer had investigated the representation theory of finite groups on finite-dimensional vector spaces over fields of characteristic p. Here, too, reducible representations need not decompose as direct sums, though in this case the problem is not lack of compactness (obviously, since everything is finite) but an inability to average over the group: we would like to divide by |G|, but often this is zero. A simple example that illustrates this is the action of /p on the space 
that takes x to the 2 × 2 matrix 
. This is reducible, since the column vector 
is fixed by the action, and therefore generates an invariant subspace. However, if one could decompose the action, then the matrices would all be diagonalizable, which they are not.
It is possible for there to be infinitely many indecomposable representations, which again may vary in families. However, as before, there are only finitely many irreducible representations, so there is some chance of a “character table is square” theorem in which the rows of the square are parametrized by characters of irreducible representations. Brauer proved just such a theorem, pairing the characters with p-semisimp1e conjugacy classes in G: that is, conjugacy classes of elements whose order is not divisible by p.
We will draw two crude morals from the work of Harish-Chandra and of Brauer. The first is that the category of representations of a group is always a reasonable object, but when the representations are infinite dimensional it requires serious technical work to set it up. Objects in this category do not necessarily decompose as a direct sum of irreducibles (one says that the category is not semisimp1e), and can occur in infinite families, but irreducible objects pair off in some precise way with certain “diagonalizable” conjugacy classes in the group—there is always some kind of analogue of “the character table is square” theorem.
It turns out that when we consider representations in more general contexts—Lie algebras acting on vector spaces, quantum groups, p-adic groups on infinite-dimensional complex or p-adic vector spaces, etc.– these qualitative features stay the same.
The second moral is that we should always hope for some “non-Abelian Fourier transform”: that is, a set that parametrizes irreducible representations and a description of the character values in terms of this set.
In the case of real reductive groups Harish-Chandra’s work provides such an answer, generalizing the Weyl character formula for compact groups; for arbitrary groups no such answer is known. For special classes of groups, there are partially successful general principles (the orbit method, Broué’s conjecture), of which the deepest are the extraordinary circle of conjectures known as the Langlands program, which we shall discuss later.
5 Interlude: The Philosophical Lessons of “The Character Table Is Square”
Our basic theorem (“the character table is square”) tells us to expect that the category of all irreducible representations of G is interesting when the conjugacyclass structure of G is in some way under control. We will finish this essay by explaining a remarkable family of examples of such groups—the rational points of reductive algebraic groups—and their conjectured representation theory, which is described by the Langlands program.
An affine algebraic group is a subgroup of some group GLn that is defined by polynomial equations in the matrix coefficients. For example, the determinant of a matrix is a polynomial in the matrix coefficients, so the group SLn, which consists of all matrices in GLn with determinant 1, is such a group. Another is SOn, which is the set of matrices with determinant 1 that satisfy the equation AAT = I.
The above notation did not specify what sort of coefficients we were allowing for the matrices. That vagueness was deliberate. Given an algebraic group G and a field k, let us write G(k) for the group where the coefficients are taken to have values in k. For example, SLn(
q) is the set of n × n matrices with coefficients in the finite field q and determinant 1. This group is finite, as is SOn(q), while SLn() and SOn() are Lie groups. Moreover, SOn() is compact, while SLn() is not. So among affine algebraic groups over fields one already finds all three types of groups we have discussed: finite groups, compact Lie groups, and noncompact Lie groups.
We can think of SLn() as the set of matrices in SLn() that are equal to their complex conjugates. There is another involution on SLn() that is a sort of “twisted” form of complex conjugation, where we send a matrix A to the complex conjugate of (A–1)T. The fixed points of this new involution (that is, the determinant-1 matrices A such that A equals the complex conjugate of (A–1)T) form a group called SUn(). This is also called a real form of SLn (),10 and it is compact.
The groups SLn(q) and SOn(q) are almost simple groups;11 the classification of finite simple groups tells us, mysteriously, that all but twenty-six of the finite simple groups are of this form. A much, much easier theorem tells us that the connected compact groups are also of this form.
Now, given an algebraic group G, we can also consider the instances G(
p), where p is the field of p-adic numbers, and also G(). For that matter, we may consider G(k) for any other field k, such as the FUNCTION FIELD OF AN ALGEBRAIC VARIETY [V.30]. The lesson of section 4 is that we may hope for all of these many groups to have a good representation theory, but that to obtain it there will be serious “analytic” or “arithmetic” difficulties to overcome, which will depend strongly on the properties of the field k.
Lest the reader adopt too optimistic a viewpoint, we point out that not every affine algebraic group has a nice conjugacy-class structure. For example, let Vn be the set of upper triangular matrices in GLn with 1s along the diagonal, and let k be q). For large n, the conjugacy classes in Vn(q) form large and complex families: to parametrize them sensibly one needs more than n parameters (in other words, they belong to families of dimension greater than n, in an appropriate sense), and it is not in fact known how to parametrize them even for a smallish value of n, such as 11. (It is not obvious that this is a “good” question though.)
More generally, solvable groups tend to have horrible conjugacy-class structure, even when the groups themselves are “sensible.” So we might expect their representation theory to be similarly horrible. The best we can hope for is a result that describes the entries of the character table in terms of this horrible structure—some kind of non-Abelian Fourier integral. For certain p-groups Kirillov found such a result in the 1960s, as an example of the “orbit method,” but the general result is not yet known.
On the other hand, groups that are similar to connected compact groups do have a nice conjugacy-class structure: in particular, finite simple groups do. An algebraic group is called reductive if G () has a compact real form. So, for instance, SLn is reductive by the existence of the real form SUn(). The groups GLn and SOn are also reductive, but Vn is not.12
Let us examine the conjugacy classes in the group SUn. Every matrix in SUn() can be diagonalized, and two conjugate matrices have the same eigenvalues, up to reordering. Conversely, any two matrices in SUn() with the same eigenvalues are conjugate. Therefore, the conjugacy classes are parametrized by the quotient of the subgroup of all diagonal matrices by the action of Sn that permutes the entries.
This example can be generalized. Any compact connected group has a maximal torus T, that is, a maximal subgroup isomorphic to a product of circles. (In the previous example it was the subgroup of diagonal matrices.) Any two maximal tori are conjugate in G, and any conjugacy class in G intersects T in a unique W-orbit on T, where W is the Weyl group, the finite group N(T)/T (where N(T) is the normalizer of T).
The description of conjugacy classes in G(
), for an algebraically closed field , is only a little more complicated. Any element g ∈ G() admits a JORDAN DECOMPOSITION [III.43]: it can be written as g = su = us, where s is conjugate to an element of T() and u is unipotent when considered as an element of GLn (). (A matrix A is unipotent if some power of A – I is zero.) Unipotent elements never intersect compact subgroups. When G = GLn this is the usual Jordan decomposition; conjugacy classes of unipotent elements are parametrized by partitions of n, which, as we mentioned in section 2, are precisely the conjugacy classes of W = Sn. For general reductive groups, unipotent conjugacy classes are again almost the same thing as conjugacy classes in W.13 In particular, there are finitely many, independent of .
Finally, when k is not algebraically closed, one describes conjugacy classes by a kind of Galois descent; for example, in GLn (k), semisimgle classes are still determined by their characteristic polynomial, but the fact that this polynomial has coefficients in k constrains the possible conjugacy classes.
The point of describing the conjugacy-class structure in such detail is to describe the representation theory in analogous terms. A crude feature of the conjugacyclass structure is the way it decouples the field k from finite combinatorial data that is attached to G but independent of k—things like W, the lattice defining T, roots, and weights.
The “philosophy” suggested by the theorem that the character table is square suggests that the representation theory should also admit such a decoupling: it should be built out of the representation theory of k*, which is the analogue of the circle, and out of the combinatorial structure of G() (such as the finite groups W). Moreover, representations should have a “Jordan decomposition”:14 the “unipotent” representations should have some kind of combinatorial complexity but little dependence on k, and compact groups should have no unipotent representations.
The Langlands program provides a description along the lines laid out above, but it goes beyond any of the results we have suggested in that it also describes the entries of the character table. Thus, for this class of examples, it gives us (conjecturally) the hoped-for “non-Abelian Fourier transform.”
6 Coda: The Langlands Program
And so we conclude by just hinting at statements. If G(k) is a reductive group, we want to describe an appropriate category of representations for G(k), or at least the character table, which we may think of as a “semisimplification” of that category.
Even when k is finite, it is too much to hope that conjugacy classes in G(k) parametrize irreducible representations. But something not so far off is conjectured, as follows.
To a reductive group G over an algebraically closed field, Langlands attaches another reductive group LG, the Langlands dual, and conjectures that representations of G (k) will be parametrized by conjugacy classes in LG().15 However, these are not conjugacy classes of elements of LG(), as before, but of homomorphisms from the Galois group of k to LG. The Langlands dual was originally defined in a combinatorial manner, but there is now a conceptual definition. A few examples of pairs (G,LG) are (GLn, GLn), (SO2n+1, Sp2n), and (SLn, PGLn).
In this way the Langlands program describes the representation theory as built out of the structure of G and the arithmetic of k.
Although this description indicates the flavors of the conjectures, it is not quite correct as stated. For instance, one has to modify the Galois group 16 in such a way that the correspondence is true for the group GL1 (k) = k*. When k = , we get the representation theory of * (or its compact form S1), which is Fourier analysis; on the other hand, when k is a p-adic local field, the representation theory of k* is described by local class field theory. We already see an extraordinary aspect of the Langlands program: it precisely unifies and generalizes harmonic analysis and number theory.
The most compelling versions of the Langlands program are “equivalences of derived categories” between the category of representations and certain geometric objects on the spaces of Langlands parameters. These conjectural statements are the hoped-for Fourier transforms.
Though much progress has been made, a large part of the Langlands program remains to be proved. For finite reductive groups, slightly weaker statements have been proved, mostly by Lusztig. As all but twenty-six of the finite simple groups arise from reductive groups, and as the sporadic groups have had their character tables computed individually, this work already determines the character tables of all the finite simple groups.
For groups over , the work of Harish-Chandra and later authors again confirms the conjectures. But for other fields, only fragmentary theorems have been proved. There is much still to be done.
Further Reading
A nice introductory text on representation theory is Alperin’s Local Representation Theory (Cambridge University Press, Cambridge, 1993). As for the Langlands program, the 1979 American Mathematical Society volume titled Automorphic Forms, Representations, and L-functions (but universally known as “The Corvallis Proceedings”) is more advanced, and as good a place to start as any.
1. By “the same” we mean “isomorphic as sets with G-action.” The casual reader may read this as “the same,” while the more careful reader should stop here and work out, or look up, precisely what is meant.
2. Exercise: go back to the example of D8 and list all the possible transitive actions.
3. THE CLASSIFICATION OF FINITE SIMPLE GROUPS [V.7] does at least allow us to estimate the number γn of subgroups of Sn up to conjugacy: it is a result of Pyber that 2((1/16)+o(1)n2 ≤ γn ≤ 24((1/6)+o(1))n2 Equality is expected for the lower bound.
4. To summarize the rest of this article: the similarity to the Fourier transform is not just analogy—decomposing a representation into its irreducible summands is a notion that includes both this example and the Fourier transform.
5. Not only is the set of all partitions a sensible combinatorial object, it is far smaller than the set of all subgroups of Sn: HARDY [VI.73] and RAMANUJAN [VI.82] showed that the number of partitions of n is about 
.
6. The homology groups discussed in the article just referred to consist of formal sums of homology classes with integer coefficients. Here, where a vector space is required, we are taking real coefficients.
7. To make this precise requires some care about what we mean by “isomorphic.” Because many different topological vector spaces can have the same underlying 2-module, the correct notion is of infinitesimal equivalence. Pursuing this notion leads to the category of Harish-Chandra modules, a category with good finiteness properties.
8. It is a major theorem of Harish-Chandra that the distribution that defines a character is given by analytic functions on a dense subset of the semisimple elements of the group.
9. The problem of determining the irreducible unitary representations for real reductive groups has still not been solved; the most complete results are due to Vogan.
10. When we say that SLn () and SUn () are both “real forms” of SLn(), what is meant more precisely is that in both cases the group can be described as a subgroup of some group of real matrices that consists of all solutions to a set of polynomial equations, and that when the same set of equations is applied instead to the group of complex matrices the result is isomorphic to SLn ().
11. Which is to say that the quotient of these groups by their center is simple.
12. The miracle, not relevant for this discussion, is that compact connected groups can be easily classified. Each one is essentially a product of circles and non-Abelian simple compact groups. The latter are parametrized by DYNKIN DIAGRAMS [III.48 § 3]. They are SUn, Sp2n, SOn, and five others, denoted E6, E7, E8, F4, and G2. That is it!
13. They are different, but related. Precisely, they are given by combinatorial data, Lusztig’s two-sided cells for the corresponding affine Weyl group.
14. The first such theorems were proved for GLn (q) by Green and Steinberg. However, the notion of Jordan decomposition for characters originates with Brauer, in his work on modular representation theory. It is part of his modular analogue of the “character table is square” theorem, which we mentioned in section 3.
15. The here is because we are looking at representations on complex vector spaces; if we were looking at representations on vector spaces over some field , we would take LG().
16. The appropriately modified Galois group is called the Weil-Deligne group.