---

IV.1 Algebraic Numbers

---

Barry Mazur

---

The roots of our subject go back to ancient Greece while its branches touch almost all aspects of contemporary mathematics. In 1801 the Disquisitiones Arithmeticae Of CARL FRIEDRICH GAUSS [VI.26] was first published, a “founding treatise,” if ever there was one, for the modern attitude toward number theory. Many of the still unachieved aims of current research can be seen, at least in embryonic form, as arising from Gauss’s work.

This article is meant to serve as a companion to the reader who might be interested in learning, and thinking about, some of the classical theory of algebraic numbers. Much can be understood, and much of the beauty of algebraic numbers can be appreciated, with a minimum of theoretical background. I recommend that readers who wish to begin this journey carry in their backpacks Gauss’s Disquisitiones Arithmeticae as well as Davenport’s The Higher Arithmetic (1992), which is one of the gems of exposition of the subject, and which explains the founding ideas clearly and in depth using hardly anything more than high school mathematics.

1 The Square Root of 2

The study of algebraic numbers and algebraic integers begins with, and constantly reverts back to, the study of ordinary rational numbers and ordinary integers. The first algebraic irrationalities occurred not so much as numbers but rather as obstructions to simple answers to questions in geometry.

That the ratio of the diagonal of a square to the length of its side cannot be expressed as a ratio of whole numbers is purported to be one of the vexing discoveries of the early Pythagoreans. But this very ratio, when squared, is 2:1. So we might—and later mathematicians certainly did—deal with it algebraically. We can think of this ratio as a cipher, about which we know nothing beyond the fact that its square is 2 (a viewpoint taken toward algebraic numbers by KRONECKER [VI.48], as we shall see below). We can write in various forms, e.g.,

and we can think of 1-i = 1-e^2πi/4 as the world’s simplest trigonometric sum; we shall see generalizations of this for all quadratic surds below. We can also view as a limit of various infinite sequences, one of which is given by the elegant CONTINUED FRACTION [III.22]

Directly connected to this continued fraction (2) is the Diophantine equation

known as the Pell equation. There are infinitely many pairs of integers (x,y) satisfying this equation, and the corresponding fractions y / x are precisely what you get by truncating the expression in (2). For example, the first few solutions are (1, 1), (2, 3), (5, 7), and (12, 17), and

Replace the ±1 on the right-hand side of (3) by zero and you get 2X² - Y² = 0, an equation all of whose positive real-number solutions (X, Y) have the ratio Y/X = , so it is easy to see that the sequence of fractions (4) (these being alternately larger and smaller than = 1.414 . . .) converges to in the limit. Even more striking is that (4) is a list of fractions that best approximate . (A rational number a/d is said to be a best approximant to a real number α if a/d is closer to α than any rational number of denominator smaller than or equal to d.) To deepen the picture, consider another important infinite expression, the conditionally convergent series

Here the n range over positive odd numbers, and the sign of the term ±1/n is plus if n has a remainder of 1 or 7 when divided by 8, and it is minus if n has a remainder of 3 or 5. This elegant formula (5), which you are invited to “check out” at least to one digit accuracy with a calculator, is an instance of the powerful and general theory of analytic formulas for special values of L-FUNCTIONS[III.4 7], which plays the role of a bridge between the more algebraic and the more analytic sides of the story. When we allude to this, below, we will call it “the analytic formula,” for short.

2 The Golden Mean

If you are looking for quadratic irrationalities that have been the subject of geometric fascination through the ages, then has a strong competitor in the number (1 + ), known as the golden mean. The ratio (1 + ):1 gives the proportions of a rectangle with the property that when you remove a square from it, as in figure 1, you are left with a smaller rectangle whose sides are in the same proportion. Its corresponding trigonometric sum description is

Its continued-fraction expansion is

where the sequence of fractions obtained by successive truncations of this continued fraction,

is a sequence of best rational-number approximants to

(1 + ) = 1.618033988749894848 . . . ,

where “best” has the sense already mentioned. For example, the fraction

equals 1.619047619047619047 . . . and is closer to the golden mean than any fraction with denominator less than 21.

Figure 1 The outer rectangle has its height-to-width ratio equal to the golden mean. If you remove a square from it as indicated in the figure, you are left with a rectangle that has the golden mean as its width-to-height ratio. This procedure is of course repeatable.

Nevertheless, the exclusive appearance of 1s in this continued fractions¹ can be used to show that, among all irrational real numbers, the golden mean is the number that is, in a specific technical sense, least well approximated by rational numbers.

Readers familiar with the sequence of Fibonacci numbers will recognize them in the successive denominators of (8), and in the numerators as well. The analogue to equation (3) is

This time, if you replace the ±1 on the right-hand side of the equation by 0, you get the equation X² + XY - Y² = 0, whose positive real-number solutions (X, Y) have the ratio Y/X = (1 + ), that is, the golden mean. And now the numerators and denominators y, x that appear in (8) run through the positive integral solutions of (9). The analogue of formula (5) (the “analytic formula”) for the golden mean is the conditionally convergent infinite sum

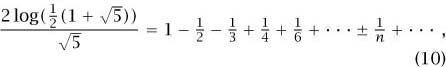
where the n range over positive integers not divisible by 5, and the sign of ±1/n is plus if n has a remainder of ^±1 when divided by 5, and minus otherwise.

What governs the choice of the plus terms and minus terms is whether or not n is a quadratic residue modulo 5. Here is a brief explanation of this terminology. If m is an integer, two integers a, b are said to be congruent modulo m (in symbols we write a ≡ b mod m) if the difference a - b is an integral multiple of m; if a, b, and m are positive numbers, it is equivalent to ask that a and b have the same “remainder” (sometimes also called “residue”) when each is divided by m (see MODULAR ARITHMETIC [III.58]). An integer a relatively prime to m is called a quadratic residue module m if a is congruent to the square of some integer, modulo m; otherwise it is called a quadratic nonresidue modulo m. So, 1, 4, 6, 9, . . . are quadratic residues modulo 5, while 2, 3, 7, 8, . . . are quadratic nonresidues modulo 5.

A generalization of equations (5) and (10) (the “analytic formula for the L-function attached to quadratic Dirichlet characters”) gives a very surprising formula for the conditionally convergent sum of terms ±1/n, where n runs through positive integers relatively prime to a fixed integer and the sign of ±1/n corresponds to whether n is a quadratic residue, or nonresidue modulo that integer.

3 Quadratic Irrationalities

The quadratic formula

gives the solutions (usually two) to the general quadratic polynomial equation aX² + bX + c = 0 as a rational expression of the number , where D = b² - 4ac is known as the discriminant of the polynomial aX² + bX + c, or, equivalently, of the corresponding homogeneous QUADRATIC FORM [III.73] aX² + bXY + cY². This formula introduces many irrational numbers: Plato’s dialogue “Theaetetus” has the young Theaetetus credited with the discovery that is irrational whenever D is a natural number that is not a perfect square. The curious switch, from initially perceiving an obstruction to a problem to eventually embodying this obstruction as a number or an algebraic object of some sort that we can effectively study, is repeated over and over again, in different contexts, throughout mathematics. Much later, complex quadratic irrationalities also made their appearance. Again these were not at first regarded as “numbers as such,” but rather as obstructions to the solution of problems. Nicholas Chuquet, for example, in his 1484 manuscript, Le Triparty, raised the question of whether or not there is a number whose triple is four plus its square and he comes to the conclusion that there is no such number because the quadratic formula applied to this problem yields “impossible” numbers, i.e., complex quadratic irrationalities in our terminology.²

For any real quadratic (“integral”) irrationality there is a discussion along similar lines to the ones we have just given (expressions (1)-(5) for and expressions (6)-(10) for (1 + )). For complex irrationalities, there is also such a theory, but with interesting twists. For one thing, we do not have anything directly comparable to continued-fraction expansions for a complex quadratic irrationality. In fact, the simple, but true, answer to the problem of how to find an infinite number of rational numbers that converge to such an irrationality is that you cannot! Correspondingly, the analogue of the Pell equation has only finitely many solutions. As a consolation, however, the appropriate “analytic formula” has a simpler sum, as we will see below.

Let d be any square-free integer, positive or negative. Associated with d is a particularly important number τ_d,defined as follows. If d is congruent to 1 mod 4 (that is, if d - 1 is a multiple of 4), then τ_d = (1 + ; otherwise, τ_d = . We will refer to these quadratic irrationalities τ_d as fundamental algebraic integers of degree 2. The general notion of an “algebraic integer” is defined in section 11. An algebraic integer of degree two is simply a root of a quadratic polynomial of the form X² + aX + b with a, b ordinary integers. In the first case (when d ≡ 1 modulo 4), τ_dis a root of the polynomial X² - X + (1 - d) and in the second it is a root of X² - d. The reason special names are given to these quadratic irrationalities is that any quadratic algebraic integer is a linear combination (with ordinary integers as coefficients) of 1 and one of these fundamental quadratic algebraic integers.

4 Rings and Fields

I think that one of the big early advances in mathematics is the now-current, universal recognition of the importance of studying the properties of collections of mathematical objects, and not just the objects in isolation. A ring R of complex numbers is a collection of them that contains 1 and is closed under the operations of addition, subtraction, and multiplication. That is, if a, b are any two numbers in R, a ± b and ab must also be in R. If such a ring R has the further property that it is closed under division by nonzero elements (i.e., if a/b is again in R whenever a and b are, and b ≠ 0), then we say that R is a field. (These concepts are discussed further in FIELDS [I.3 §2.2] and RINGS, IDEALS, AND MODULES [III.81].) The ring of ordinary integers, {0, ±1, ±2,. . . } is our “founding example” of a ring; visibly, it is the smallest ring of complex numbers.

The collection of all real or complex numbers that are integral linear combinations of 1 and τ_d is closed under addition, subtraction, and multiplication, and is therefore a ring, which we denote by R_d. That is, R_d is the set of all numbers of the form a + bτ_d where a and b are ordinary integers. These rings R_d are our first, basic, examples of rings of algebraic integers beyond that prototype, , and they are the most important rings that are receptacles for quadratic irrationalities. Every quadratic irrational algebraic integer is contained in exactly one R_d.

For example, when d = -1 the corresponding ring R_-1, usually referred to as the ring of Gaussian integers, consists of the set of complex numbers whose real and imaginary parts are ordinary integers. These complex numbers may be visualized as the vertices of the infinite tiling of the complex plane by squares whose sides have length 1 (see figure 2).

When d = -3 the complex numbers in the corresponding ring R_-3 may be visualized as the vertices of a tiling of the complex plane by equilateral triangles (see figure 3).

With the rings R_d in hand, we may ask ring-theoretic questions about them, and here is some of the standard vocabulary useful for this. A unit u in a given ring R of complex numbers is a number in R whose reciprocal 1/u is also in R; an irreducible element in R is a nonunit that cannot be written as the product of two nonunits in R. A ring of complex numbers R has the unique factorization property if every nonzero, nonunit, algebraic number in R can be expressed as a product of irreducible elements in exactly one way (where two factorizations are counted as the same if one can be obtained from the other by rearranging the order in which the irreducible elements appear and multiplying them by units).

Figure 2 The Gaussian integers are the vertices of this lattice of squares tiling the complex plane.

Figure 3 The elements of the ring R_-3 are the vertices of this lattice of equilateral triangles tiling the complex plane.

In the prototype ring of ordinary integers, the only units are ±1 and the irreducible elements are all numbers of the form ±p with p prime. The fundamental fact that any ordinary integer greater than 1 can be uniquely expressed as a product of (positive) prime numbers (that is, that enjoys the unique factorization property) is crucial for much of the number theory done with ordinary integers. That this unique factorization property for integers actually required proof was itself a hard-won realization of Gauss, who also provided its proof (see THE FUNDAMENTAL THEOREM OF ARITHMETIC [V.14]).

It is easy to see that there are only four units in the ring R_-1 of Gaussian integers, namely ±1 and ±i; multiplication by any of these units effects a symmetry of the infinite square tiling (figure 2 above). There are only six units in the ring R_-3, namely ±1, ± (1 + ) and ± (1 - ,); multiplication by any of these units results in a symmetry of the infinite triangular tiling illustrated in figure 3.

Fundamental to understanding the arithmetic of R_d is the following question: which ordinary prime numbers p are irreducible elements of R_d and which ones factorize as products of irreducible elements in R_d? We will see shortly that if a prime number does factorize in Rd, it must be expressible as the product of precisely two irreducible factors. For example, in the ring of Gaussian integers, R_-1, we have the factorizations

2 = (1 + i)(1 - i),
5 = (1 + 2i)(1 - 2i),
13 = (2 + 3i)(2 - 3i),
17 = (1 + 4i)(1 - 4i),
29 = (2 + 5i)(2 - 5i),

where all the Gaussian integer factors in brackets above are irreducible elements of the ring of Gaussian integers.

Let us say that an odd prime p splits in R_-1 if it factorizes into a product of at least two primes and remains prime if it does not do so. As we shall soon see, the officially agreed-upon definitions of splitting and remaining prime for more general rings of algebraic integers (even ones of the form R_d) are worded slightly, but very significantly, differently from the way we have just defined these concepts in the ring R_-1 of Gaussian integers. (Note that we have excluded the prime p = 2 from the above dichotomy. This is because 2 ramifies in R_-1; for a discussion of this concept see section 7 below.) In any event, there is an elementary computable rule that tells us, for any R_d, which primes p split and which remain prime in this agreed sense. The rule depends upon the residue of p modulo 4d: the reader is invited to guess it for the ring of Gaussian integers given the data just displayed above. In general, an elementary computable rule that says which primes split and which do not in a ring of algebraic integers such as R_d is referred to as a splitting law for the ring of algebraic integers in question.

5 The Rings Rd of Quadratic Integers

There is a very important “symmetry,” or ALRROMORPHISM [I.3 §4.1], defined on the ring R_d. It sends to - , keeps all ordinary integers fixed, and more generally, for rational numbers u and υ, it sends α = u + υ to what we may call its algebraic conjugate α′ = u - υ . (The word “algebraic” is to remind you that this is not necessarily the same as the complex-conjugate symmetry of the complex numbers!)

You can immediately work out the formulas for this algebraic conjugation operation on the fundamental quadratic irrationalities τ_d: if d is not congruent to 1 modulo 4, then τ_d = so obviously = -τ_d, while if d is congruent to 1 modulo 4, then τ_d = (1 + ) and = (1- = 1 - τ_d This symmetry α α′ respects all algebraic formulas. For example, to work out the algebraic conjugate of a polynomial expression like αß + 2γ², where α, ß and γ are numbers in R_d, you just replace each individual number by its algebraic conjugate, obtaining the expression α′ß′ + 2γ^′2.

The most telling integer quantity attached to a number α = x + yτ_d in R_d is its norm N (α), which is defined to be the product αα′. This equals x² - dy² when τ^d = and x² + xy- (d-1)y² when τ_d = (1 + ). The norm turns out to be multiplicative, meaning that N(αß) = N(α)N(ß), as you can directly check by multiplying out the formula for the norm of each factor and comparing with the norm of the product. This gives us a useful tactic for trying to factorize algebraic numbers in R^d, and offers criteria for determining whether a number α in R^d is a unit, and whether it is prime in R^d. In fact, an element α ∈ R_d is a unit if and only if N(α) = αα′ = ±1; in other words, the units are given by the integral solutions to the equations

or

following the two cases. Here is the proof of this. If α = x = x + yτ_d is a unit in R_d, then its reciprocal, ß = 1 / α, must also be in R_d, and, of course, we have αß = 1. Applying the norm to both sides of this equation and using the multiplicative property discussed above, we see that N(α) and N(ß) are reciprocal ordinary integers. Therefore, they are either both equal to + 1 or both equal to -1. This shows that (x,y) is a solution to whichever of equation (11) or (12) is appropriate. In the other direction, if N(α) = αα′ = ±1,then the reciprocal of α is simply ±α′. This is in R_d so α is indeed a unit in R_d.

These homogeneous quadratic forms, the left-hand sides of equations (11) and (12) (which generalize formulas (3) and (9)), play an important role; let us refer to whichever of them is relevant to R_d as the fundamental quadratic form for R_d, and to its discriminant D as the fundamental discriminant. (D is equal to d if d is congruent to 1 modulo 4 and to 4d otherwise.) When d is negative there are only finitely many units (if d < -3 the only ones are ±1) but when d is positive, so that R_d consists entirely of real numbers, there are infinitely many. The ones that are greater than 1 are powers of a smallest such unit, ε_d, and this is called the fundamental unit.

For example, when d = 2 the fundamental unit, ε₂, is 1 + , and when d = 5 it is the golden mean, ε₅ = (1 + ). Since any power of a unit is again a unit, we immediately have a machine for producing infinitely many units from any single one. For example, taking powers of the golden mean, we get

all of which are units in R₅. The study of these fundamental units was already under way in the twelfth century in India, but in general their detailed behavior as d varies still holds mysteries for us today. For example, there is a deep theorem of Hua (1942) that tells us that ε_d < (4e²d) (for a proof of it along with a historical discussion of such estimates, see chapters 3 and 8 in Narkiewicz (1973)). There are examples of d that come close to attaining that bound, but we still do not know whether or not there is a positive number η and an infinity of square-free d for which ε_d > d^dn. (The answer to this question would be yes if, for example, there were an infinity of R_d satisfying the unique factorization property! This follows from a famous theorem of Brauer (1947) and Siegel (1935); for a proof of the Brauer-Siegel theorem, see theorem 8.2 of chapter 8 in Narkiewicz (1973) or Lang (1970).)

6 Binary Quadratic Forms and the Unique Factorization Property

The principle of unique factorization is an all-important fact for the ring of ordinary integers . The question of whether this principle does or does not hold for a given ring R_d is central to the algebraic number theory. There are helpful, analyzable, obstructions to the validity of unique factorization in R_d. These obstructions, in turn, connect with profound arithmetic issues, and have become the focus of important study in their own right. One such mode of expressing the obstruction to unique factorization is already prominent in Gauss’s Disquisitiones Arithmeticae (1801), in which much of the basic theory of R_d was already laid down.

This “obstruction” has to do with how many “essentially different” binary quadratic forms aX² + bXY + cY² there are with discriminant equal to the fundamental discriminant D of R_d. (Recall that the discriminant of aX² + bXY + cY² is b² - 4ac, and that D equals 4d unless d ≡ 1 mod 4, in which case it equals d.)

In order to define a binary quadratic form aX² + bXY + cY² of discriminant D, what you need to provide is simply a triplet of coefficients (a, b, c) such that b² -4ac = D. Given such a form, one can use it to define other ones. For example, if we make a small linear change of the variables, replacing X by X - Y and keeping Y fixed, then we get a(X - Y)² + b (X - Y)Y + cY², which simplifies to aX² + (b -2a)XY + (c - b + a)Y². That is, we get a new binary quadratic form whose triplet of coefficients is (a, b — 2a, c — b + a), and which (as can easily be checked) has the same discriminant D. We can “reverse” this change by replacing X by X + Y and keeping Y fixed. If we do this reversal and perform the corresponding simplification then we get back our original binary quadratic form. Because of this reversibility, these two quadratic forms take exactly the same set of integer values as X and Y vary: it is therefore reasonable to think of them as equivalent.

More generally, then, one says that two binary quadratic forms are equivalent if one can be turned into the other (or minus the other) by any “reversible” linear change of variables with integer coefficients. That is, one chooses integers r, s, u, v such that rυ - su = ±1, replaces X and Y by the linear combinations X′ = rX + sY, Y′ = uX + υY, and simplifies the resulting expression to get a new triplet of coefficients. The condition rυ - su = ±1 guarantees that by a similar operation we can get back to our original binary quadratic form, and also that the new binary quadratic form has the same discriminant D as the old one. So when we talk of “essentially different” binary quadratic forms of discriminant D we mean that we cannot turn one into the other by this kind of change of variables.

Here is the surprising obstruction to unique factorization that Gauss discovered.

The unique factorization principle is valid in R_d if and only if every homogeneous quadratic form aX² + bXY + cY² with discriminant equal to the fundamental discriminant of R_d is equivalent to the fundamental quadratic form of R_d.

Furthermore, the collection of inequivalent quadratic forms whose discriminant is the fundamental discriminant of R_d expresses in concrete terms the degree to which R_d “enjoys unique factorization.”

If you have never seen this theory of binary quadratic forms before, try your hand at working with quadratic forms in the case where D = -23. The idea is to start with some particular quadratic form aX² + bXY + cY² of your choice with discriminant D = b² - 4ac = -23. Then, using a sequence of carefully chosen linear changes of variables you reduce the size of the coefficients a, b, and c until you can go no further. Eventually you should end up with one of the two (inequivalent) quadratic forms that there are with discriminant -23: the fundamental form X² + XY + 6Y², or the form 2X² + XY + 3Y². For example, can you see that the binary quadratic form X² + 3XY + 8Y² is equivalent to X² + XY + 6Y²?

This type of exercise offers a small hint of the role that the geometry of numbers will play in the eventual theory. As you might expect from the venerability of these ideas, elegant streamlined methods have been discovered for making such calculations. Nevertheless, it is an open secret that any working mathematician, contemporary or ancient, engaged in this subject or nearby subjects, has done a myriad of straightforward simple hand computations along the lines of the above exercise.

If you try a few examples of this exercise, as I hope you do, here is one way of organizing your calculations. First, find a simple reversible linear change of variables to turn your form into an equivalent one with a, b, c ≥ 0. (You may also have to multiply the whole form by-1.)

The cleanest way of writing down all binary quadratic forms given by triplets (a, b, c) of discriminant -23 is to list the triplets in increasing order of b, which will now be an odd positive integer. For each value of b you can then choose a and c in such a way that their product is (b² + 23). At this point the aim is to build up a repertoire of moves that tend to decrease b (which will keep a and c within bounds as well). A big clue, and aid, here is that for any pair of relatively prime integers x,y if you evaluate your quadratic form aX² + bXY+ cY² at (X, Y) = (x,y) to get the integer a′ = ax²+bxy+cy², you can find, for appropriate b′ and c′, a quadratic form a′X² + b′XY + c′Y² equivalent to yours, with first coefficient a′. So, one tactic is to look for small integers represented by your quadratic form. Also the “example” linear change of variables X X – Y, Y Y will lead you to be able to reduce the coefficient b to an integer smaller than 2 a. Can you check that X² + XY + 6Y² and 2X² +XY + 3Y² are inequivalent?

Now, as we have just discussed, it follows from the general theory that R_-23 does not have the unique factorization property. We can also see this directly. For example,

τ_-23 · τ′_-23 = 2 . 3,

and all four of the factors in this equation are irreducible in R_-23. To be a faithful companion, I should at this point give at least a hint at what connection there might be between this specific “failure of unique factorization” and the previous discussion. It may become a bit clearer in the next paragraph, but the underlying tension in the equation τ_-23· τ′_-23 = 2 · 3 is that all the factors in our ring are prime: we are missing any elements in our ring R_-23 that could factorize it further. We lack, for example, elements that play the role of the greatest common divisor of factors of this equation. The general theory regarding these matters (which we are not entering into here, but see EUCLID’S ALGORITHM [III.22]) tells us that what is missing is some element y in R_-23 that is both a linear combination of the numbers τ_-23 and 2 (with coefficients in the ring R_-23) and also a common divisor of τ_-23 and 2 in the ring R·_-23, i.e., such that τ_-23/γ and 2/γ are both in R_-23. There is no such element, for its norm must divide N(τ₂₃) = 6 and N(2) = 4, and therefore be equal to 2, which can easily be shown to be impossible. But we are interested, rather, in the phenomenon that inequivalence of certain binary quadratic forms will indeed show this, so let us go on.

First, check that any linear combination

α · τ_-23 + ß·2

with α, ß elements of R_-23 can also be written as u · τ_-23 + υ·2, where u and υ are ordinary integers. Now compute the binary quadratic form given by systematically taking the norms of these linear combinations, and viewing these norms as functions of the integer coefficients u, υ:

Viewing the u and the υ as variables, and dubbing them U and V to emphasize their status as variables, we can say that the norm quadratic form obtained from the collection of linear combinations of τ_-23 and 2 is

6U² + 2UV + 4V² = 2 · (3U² + UV + 2V²).

Now suppose that, contrary to fact, there were a common divisor, γ, as above; in particular, the multiples of γ in the ring R_-23 would then be precisely the linear combinations of the numbers τ_-23 and 2. We would then have another way of describing those linear combinations; namely, for any pair of ordinary integers (u, υ) there would be a pair of ordinary integers (r, s) such that

u · τ_-23 + υ · 2 = γ · (rτ_-23 + s) = rγτ_-23 + sγ.

Taking norms, as above, we would get

Again, thinking of r and s as variables and renaming them R and S we would have the corresponding norm quadratic form:

N(γ) · (6R² + RS + S²) = 2 · (6R² + RS + S²).

Given the above facts—dependent, of course, on the contrary-to-fact hypothesis that there is a γ as above— the key idea is that there would be linear changes of variables from (U,V) to (R, S) and back that would establish an equivalence between the two quadratic forms 2 · (3U² + UV + 2V²) and 2 · (6R² + RS + S²). But these quadratic forms are not equivalent! Their inequivalence therefore shows that the putative γ does not exist and factorization in the ring R_-23 is not unique.

7 Class Numbers and the Unique Factorization Property

In the previous section we saw that the collection of inequivalent quadratic forms of discriminant equal to the fundamental discriminant provides us with an obstruction to unique factorization. Somewhat later, a more articulated version of this obstruction arose, known as the ideal class group H_d of R_d. As its name implies, to describe this we must use the vocabulary of IDEALS [III.81 §2] and GROUPS [I.3 §2.1]. A subset I of Rd is an ideal if it has the following closure properties: if α belongs to I, so do –α and τ_dα, and if α and ß belong to I, so does α + ß. (The first and third properties imply together that any integer combination of a and ß belongs to I.) The basic example of such an ideal is the set of all multiples of some fixed, nonzero element γ of R_d, where by a multiple of γ we mean the product of γ and an element of R_d. We denote this set tersely as (γ), or, slightly more expressively, as γ · R_d. An ideal of this sort, i.e., one that can be expressed as the set of all multiples of a single nonzero element γ, is called a principal ideal. For example, the ring R_d itself is an ideal (it consists, after all, of all linear combinations of 1 and τ_d) and is even a principal ideal: in our laconic terminology, it can be denoted (1) = 1 · R_d = R_d. Strictly speaking, the singleton {0} is also an ideal, but the ones that will interest us are the nonzero ideals.

As a direct counterpart to the obstruction principle involving binary quadratic forms that was described in the previous section, we have the following obstruction principle involving ideals.

The unique factorization principle is valid in R_d if and only if every ideal in R_d is principal.

Reflecting on this, you can get a sense of why the word “ideal” might have been chosen. Every principal ideal in R_d is of the form γ · R_d for some number γ in R_d (which is uniquely determined apart from multiplication by units), but sometimes there are more general ideals. These arise if you ever have two elements of R_d (think of τ_-23 and 2, as in the previous section) such that the set of all their integer combinations cannot be expressed as the set of multiples of some fixed number γ in R_d. This phenomenon is a sign that we may be missing numbers in R_d that provide fine enough factorizations to make the arithmetic in R_d as smooth going as one might hope for. Just as a principal ideal γ · R_d corresponds to the number γ, ideals of this more general kind (think of the set of all integer combinations of τ_-23 and 2) can be thought of as corresponding to “ideal numbers” that should, by rights,” be present in our ring, but happen not to be.

Once we think of ideals as standing for ideal numbers it makes some sense to try to multiply them: if I, J are two ideals in R_d, we let I · J denote the set of all finite sums of products α · ß in which a is in I and ß is in J. The product of two principal ideals (γ_l) · (γ₂) is the principal ideal (γ₁ · γ₂) so, just as one would hope, multiplication of principal ideals corresponds to multiplication of the corresponding numbers. Multiplication of any ideal ? by the ideal (1) leaves I unchanged: (1) .1 = I; we therefore refer to the ideal (1) as the unit ideal. With this new notion of multiplication of ideals we can now give the general definition of what it means for a prime number p to split or to remain prime in a ring R_d, the definition we promised in section 4.

The idea behind the definition is to use multiplication of ideals rather than of numbers. So if we are thinking about a prime p, the first thing we do is turn our attention to the principal ideal (p) in R_d. If this can be factorized as a product of two different ideals (not necessarily principal ideals, this is the whole point) in R_d, and if neither of these is the unit ideal (1) = R_d, then we say that p splits in R_d. If, on the other hand, no factorization of the ideal (p) can be made without one of the factors being the ideal (1) = R_d, then we say that p remains prime in R_d. There is also a third important definition: if the principal ideal (p) can be expressed as the square of another ideal I, then we say that p ramifies in Rd. Continuing with the momentum of this definition, we may say that an ideal P is a prime ideal if P cannot be “factorized” as the product of two ideals neither of which is the unit ideal. This definition makes sense whether or not P is principal, so we are subtly shifting our attention from the multiplicative arithmetic of the numbers in R_d to the ideals.

By definition, two ideals are in the same ideal class if when you multiply each by an appropriate principal ideal you get the same ideal as a result. This is a natural EQUIVALENCE RELATION [I.2 §2.3] on ideals. It is also one that respects products, meaning that if I and J are two ideals, then the ideal class of their product I · J depends only on the ideal classes of I and J. (In other words, if I′ is in the same ideal class as I and J´ is in the same ideal class as J´, then I´ · J´ is in the same ideal class as I · J.) We can therefore say what we mean by multiplication of ideal classes: to multiply two classes, pick an ideal from each, multiply those, and take the ideal class of the resulting product. The set H_d of ideal classes of R_d, given this operation of multiplication, forms an Abelian group, in the sense that the multiplication law we have just defined is associative and commutative, and there are inverses. The identity element is the principal ideal R_d itself. This group H_d, the ideal class group, directly measures the extent to which the ideals of the ring R_d are principal: roughly speaking it is what you get if you take the multiplicative structure of all ideals and “divide out” by the principal ones.

As was mentioned in section 6, there is a close connection between ideal classes and binary quadratic forms. To begin to see this, take an ideal I of R_d and write it as the set of all integer combinations of two elements α, ß of R_d. Then consider the norm function on the elements of I, that is,

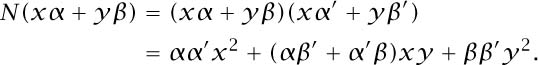
This is a binary quadratic form in the variable coefficients x and y. If you start with a different choice of ο,that generate I you get a different form, but the two forms are scalar multiples of two forms with discriminant D that are equivalent to one another. Even better, the equivalence class of these forms depends only on the ideal class of I.

It can be shown that there are only a finite number of distinct ideal classes of R_d; that is, the ideal class group H_d is finite. The number of its elements is denoted h_d and called the class number of R_d. So, the obstruction to unique factorization of Rd is given by the nontriviality of the group H_d; equivalently, unique factorization holds for R_d if and only if its class number is 1. But whether or not H_d is trivial, its detailed group-theoretic structure is profoundly related to the arithmetic of Rd.

The class number enters into the generalizations of formulas (5) and (10) of section 1; that is, the analytic formulas we alluded to in that section. These formulas represent just the beginning of one of the ongoing chapters of our subject, and form a bridge between the world of discrete arithmetical issues and that of calculus, infinite series, and volumes of spaces, all of which can be attacked by the methods of COMPLEX ANALYSIS [I.3 §5.6]. Here is a sample of them.

(i) If d > 0 is a square-free integer and D is either d or 4d according to whether d is congruent to 1 modulo 4 or not, then

  where the integers n run through those that are relatively prime to D and the signs ± are chosen in a way that depends only on the residue class of n modulo D.

(ii) If d < 0 we have a somewhat simpler formula: there is no fundamental unit εd in R_d to contend with, but when d = -1 or -3, there are more roots of unity than merely ±1. If w_d denotes the number of roots of unity in R_d, then w_-1 = 4, w_-3 = 6 and otherwise w_d = 2, and then one has a formula of the following type:

  As d tends to ^-∞ the class number h_d tends to infinity

We have effective lower bounds for the growth of h_d but these lower bounds are probably still far from the actual growth (cf. Goldfeld 1985). The effective lower bounds that are known are exceedingly weak. They follow, however, from beautiful work of Goldfeld, and of Gross and Zagier: for every real number r < 1 there is a computable constant C(r) such that h_d > C(r) log |D|^r. Here is a sample:

if (D,5077) = 1.

It is a striking lacuna in our theory that, even today, nobody knows how to prove that there are infinitely many values of d > 0 for which R_d enjoys the unique factorization property—particularly since we expect that more than three quarters of them do! Our expectations are even more precise than that, thanks to Henri Cohen and Hendrik Lenstra, who make use of certain probabilistic expectations (now known as the Cohen-Lenstra heuristics) to conjecture that the density of positive fundamental discriminants of class number 1 among all positive fundamental discriminants is 0.75446 . . . .

8 The Elliptic Modular Function and the Unique Factorization Property

A different obstruction to unique factorization in R_d is available when d is negative. Now R_d may be thought of as a lattice in the complex plane (see figure 3), which makes a wonderful tool available for us: the classical elliptic modular function of KLEIN [VI.57],

This function, also colloquially referred to as the “j-function,” converges for complex numbers z = x + iy with y > 0. If z = x + iy and z′ = x′ + iy′ are two such complex numbers, then j(z) = j(z′) if and only if the lattice generated by z and 1 in the complex plane is the same as the lattice generated by z′ and 1 (or, equivalently, z′ = (az + b)/(cz + d), where a, b, c, and d are ordinary integers such that ad - bc = 1). We can paraphrase this by saying that the value j(z) depends only on, and characterizes, the lattice generated by z and 1.

It turns out (by a theorem of Schneider) that if an algebraic number α = x + iy with y > 0 has the property that j(α) is also algebraic, then α is a (complex) quadratic irrationality; and the converse is also true. In particular, since α = τ_d is such a complex quadratic irrationality when d is negative, the value, j(τ_d), of the j-function on τd is an algebraic number—in fact, an algebraic integer. This will be of some importance for our story. First, since the ring R_d as situated in the complex plane is simply the lattice generated by τ_d and 1, it follows from the previous paragraph that this value j(τ_d) will be the same if we replace τ_d by any element α of R_d, as long as the lattice generated by a and 1 is the entire ring R_d. More importantly, j(τ_d) is an algebraic integer of degree roughly comparable with the class number of R_d. In particular, it is an ordinary integer if and only if the ring R_d has the unique factorization property. (This result is one of the great applications of a classical theory known as complex multiplication.) In brief, here is yet another answer to the question of when the unique factorization principle holds for R_d when d is negative: if j(τ_d) is an ordinary integer, the answer is yes; otherwise it is no.

The search for the full list of negative values of d for which R_d has the unique factorization property makes a marvelous tale: there are precisely nine values of d for which it occurs (see below), but for over two decades number theorists, while knowing these nine, could prove only that there were no more than ten. The history of how the nonexistence of a possible tenth value of d was established, and reestablished, is one of the thrilling chapters in our subject. K. Heegner, in an article published in 1952, provided what he claimed was a proof of the nonexistence of the possible tenth value of d. However, Heegner’s proof was framed in somewhat unfamiliar language and was not understood by the mathematicians of the time. His paper and his purported proof were largely forgotten until the late 1960s, when the nonexistence of the tenth field was established (to the mathematical community’s satisfaction) by Stark (1967) and independently, via a different method, by Baker (1971). It was only then that mathematicians took a second and closer look at Heegner’s original article and discovered that he had indeed proven exactly what he claimed. Moreover, his proof offered an elegant direct conceptual road to an understanding of the underlying issue.

Here are the nine values of d:

d = -1, -2, -3, -7, -11, -19, -43, -67, -163.

And here are the corresponding nine values of j(τ_d):

As Stark once pointed out, if, for some of these values of d, you simply “plug” τ_d into the power-series expansion for j, you get rather surprising formulas. For example, when d = -163, then

e^-πiτd = -e^π

is the first term of the power series for j(τ_-163) (see formula (13)). Since j(τ_-163) = -2^l83³5³23³29³ and since all the terms e^2πnτd (n > 0) that appear in the power series for the j-function are relatively small, we find that e^π is incredibly close to an integer. Indeed, it is 2¹⁸3³5³23³29³ + 744 + · · ·, which works out as 262 537412 640 768 744 - ∈, where the error term ∈ is less than 7.5 × 10^-13.

9 Representations of Prime Numbers by Binary Quadratic Forms

More often than you might expect, it turns out to be possible to translate difficult and/or somewhat artificial problems about ordinary integers into natural and tractable problems about larger rings of algebraic integers. My favorite elementary example of this type is the theorem due to FERMAT [VI.12] that if a prime number p may be expressed as a sum of two squares, p = a² + b² with 0 < a ≤ b, then it has only one such expression. (For example, 1² + 10² is the only way of expressing the prime number 101 as the sum of two squares.) Moreover, a prime number p can be expressed as a sum of two squares if and only if p = 2 or p is of the form 4k + 1. (The “only if” part of this is easy to see: since any square is congruent either to 0 or to 1 mod 4, an odd integer that is a sum of two squares is necessarily congruent to 1 mod 4.) These statements about ordinary integers can be translated into basic statements about the ring of Gaussicn integers. For if we write a² + b² = (a + ib) (a - ib), with i = , then we can view a² + b₂ as the norm of the (conjugate) elements a ± ib in the ring of Gaussicn integers. So, if p is a prime number that admits an expression as a sum of squares, p = a² + b², it follows that each of the elements a ± ib has norm a prime integer. It is easy to deduce that a±ib is itself a prime in the ring of Gaussian integers. Indeed, any factorization of a ± ib into a product of two Gaussicn integers would have the property that the norms of the factors are ordinary integers which multiply out to be the prime p, and this severely limits their possibilities: one of them has to be a unit.

In other words, whenever p = a² + b², then

p = (a + ib) (a - ib)

is a factorization of the ordinary integer prime p into a product of two Gaussicn integer primes. The uniqueness part of Fermat’s theorem then follows from (in fact, it is readily seen to be equivalent to) the unique factorization property of the ring R_-1 of Gaussian integers. That any prime number p of the form 4k + 1 admits such an expression as a sum of two squares follows from the splitting law for primes p in the ring of Gaussicn integers: an odd prime number p is a norm, and hence splits into the product of two distinct primes, in the ring of Gaussicn integers if and only if p is congruent to 1 mod 4. This result is just the beginning of an immense chapter of arithmetic.

10 Splitting Laws and the Race between Residues and Nonresidues

The simple splitting law for ordinary prime integers p in the ring of Gaussicn integers, which states that p splits if p ≡ 1 mod 4 and not if p ≡ -1 mod 4, invites us to ask how often each of these cases occurs (see figure 4). DIRICHLET [VI.36] proved a famous theorem that says that there are infinitely many primes in the arithmetic progression c, m + c, 2m + c, . . . if the integers m and c are relatively prime. A more precise version of his result gives a clear asymptotic answer to the question we have just asked: as x goes to infinity, the ratio of the number of primes less than x that split to the number that do not tends to 1. (See ANALYTIC NUMBER THEORY [IV.2 §4] for a further discussion of Dirichlet’s theorem.)

For fun, one might ask a fussier question: which type of prime less than x is actually in greater abundance, the nonsplit primes or the split ones (see figure 4)? To put some perspective on this, let us widen our query: for q equal either to 4 or to an odd prime, let A(x) be the number of primes < x that are quadratic residues modulo q and let B(x) be the number of primes < x that are quadratic nonresidues modulo q. Let D(x) = A(x) - B(x) be the difference; what does D(x) look like?

For an absorbing account of the history and status of this problem, see Granville and Martin (2006).

11 Algebraic Numbers and Algebraic Integers

Now that we have seen the algebraic integers j(τ_d) for negative values of d, and have touched on trigonometric sums, we have a few hints that, as with ordinary integers, the deep structure of these rings of quadratic integers may be better understood within a larger context of algebraic numbers. So now let us deal with algebraic numbers in full generality.

Figure 4 The higher of the two graphs in the figure represents the number of primes less than X that remain prime in the ring of Gaussian integers, and the lower represents the number of primes less than X that split in the ring of Gaussian integers. The third graph hovering around the x-axis represents the difference between the two numbers. We thank William Stein for this data.

By a monic polynomial, we mean a polynomial of the form

P(X) = Xⁿ + a¹X^n-1 + · · · + _a-1X +a_n,

i.e., a polynomial of degree n such that the coefficient of Xⁿ is 1. In general, the other coefficients are just assumed to be complex numbers. If P(X) = Xⁿ + a₁X^n-1 + · · · + a_n-1X + a_n is such a polynomial, and if Θ is a complex number such that P(Θ) = 0, or, equivalently, if Θ satisfies the polynomial equation

Θⁿ + a₁Θ^{n -1} + · · · + a_n-1Θ + a_n = 0,

we say that Θ is a root of the polynomial P(X). THE FUNDAMENTAL THEOREM OF ALGEBRA [V.13], initially proved by Gauss, guarantees that any such polynomial of degree n factors into a product of n linear polynomials. That is,

P(X) = (X - Θ₁)(X - Θ ₂) ··· (X - Θ_n)

for some complex numbers Θ₁, Θ₂, . . . , Θ_n that are in fact precisely the roots of the polynomial P(X).

If Θ is a root of such a polynomial P(X) = Xⁿ + a₁X^n-1 + ··· + a_n-1X + a_n and if in addition the coefficients a_i are rational numbers, then Θ is called an algebraic number. If the coefficients are not just rational but are in fact integers, then Θ is called an algebraic integer. So, for example, the square root of any rational number is an algebraic number and the square root of any “ordinary” integer is an algebraic integer. The same holds true for nth roots of ordinary integers, or of algebraic integers, for any natural number n. For an example of a different sort, we have already mentioned the theorem that the values of the j-function on complex quadratic irrational integers are algebraic integers. For a (random) particular case of that theorem, the complex number j(τ_-23) is a root of the monic polynomial

X³ + 3 491 750X² - 5 151 296 875X + 12 771 880 859 375.

An exercise: show that any algebraic number can be expressed as an algebraic integer divided by an ordinary integer.

12 Presentation of Algebraic Numbers

In dealing with any mathematical concept, we confront, in one way or another, the dual problem of the various forms in which it comes to us when it arises in our work, and the various ways we can present it so as to deal with it effectively. We have already seen a bit of this at the outset of this article, in our discussion of quadratic surds, and we will continue to see it in our treatment of them below, where the various modes in which quadratic surds can be presented—as radicals, as eventually recurrent continued fractions, or as trigonometric sums—come together, all contributing to their unified theory.

This issue of presentation is all the more of a problem with algebraic numbers in general, which may come to us in a multitude of ways. For example, they can arise as the coordinates of points on specific algebraic varieties whose defining equations may not be easily available, or as special values of functions like the j-function. It is natural, then, to look for some uniform way of presenting algebraic numbers, and the history of the subject shows how much effort has been devoted to such a search. For example, consider the focus on iterated radical expressions, as in the famous formula for the solution to the general cubic equation X³ = bX + c given by

or the corresponding general solution to the fourth- degree equation. These were major achievements of sixteenth-century Italian algebra, and they culminated in the proof that the general fifth-degree algebraic number could not be so expressed, which was a major achievement of the early nineteenth century (see THE INSOLUBILITY OF THE QUINTIC [V.21]). The challenge to give some analytic expression for such fifth-degree algebraic numbers was the source of a classic book by Klein, The Icosahedron, written in the late nineteenth century. Kronecker wrote that it was the “dream of his youth” (his Jugendtraum) to establish a uniform mode of presentation for a class of algebraic numbers that interested him, by expressing them as values of certain analytic functions.

13 Roots of Unity

A central role in the theory of algebraic numbers is played by the roots of unity, that is, the n complex solutions of the equation Xⁿ = 1, or equivalently the n roots of the polynomial Xⁿ – 1. If we let ζ_n = e^2πi/n, then these roots are precisely ζ_n and its powers, so in particular they are algebraic integers. They give us the factorization

Now the powers of ζ_n form the vertices of a regular n- gon in the complex plane, centered at the origin. This has the following consequence, noticed by Gauss in his youth. It can be shown that compass and straightedge constructions allow us, in effect, to extract square roots, so whenever ζ_n can be given as an expression built out of just square roots and the usual arithmetical operations, we have, implicitly, a ruler-and-compass construction of the regular n-gon, and conversely.

To get some idea of why square roots are so closely connected with these constructions, consider this. If we have given ourselves a unit measure, which we can view as the distance between the numbers 0 and 1 in the (complex) plane, and if we have already constructed, by whatever device, a specific point, x say, between 0 and 1 on the horizontal axis of the plane, we can first “construct” x/4 by straightedge and compass, and then go on to form a right-angled triangle with hypotenuse of length 1 + x/4 and one of its other sides of length 1 — x/4 (again using a straightedge and compass). The Pythagorean theorem gives us that the third side of that triangle is of length . If one follows this line of thought (but adapts it to deal with complex quantities as well as the real number x as in the example we have just discussed), then one can see that the equations

provide (implicit) constructions of the equilateral triangle, the square, the regular pentagon, and the regular hexagon, respectively. By contrast, ζ₇ cannot be expressed solely in terms of the arithmetical operations and square roots (it is the root of a quadratic equation with coefficients that are rational expressions in the roots of the irreducible cubic polynomial X³ - X + ), which already suggests that the regular heptagon might fail to be constructible by the standard classical means—and indeed it does fail without some act of “angle trisection.” (In principle, though, the reader can work out an expression for ζ7 in terms of square roots and cube roots by means of the information provided in the parenthetical phrase above, together with equation (14).)

Gauss showed that if n > 2 is a prime number then the regular n-gon is classically constructible if and only if n is a Fermat prime, that is, a prime number of the form 2^2a + 1. So, for example, the 11-gon and 13-gon are not constructible by classical means, but since ζ_l7 is expressible as nested rational expressions of square roots, the 17-gon is, famously, constructible.

So, not all roots of unity can be expressed as iterated rational expressions of square roots. However, this inhospitability is not mutual, since all square roots of integers can be expressed as integer combinations of roots of unity. More mysteriously, the elusive fundamental units ε_d (for d positive), for which there is no known formula, are intimately related to a unit C_d in R_d which is an explicit rational expression of roots of unity. (See below: it is called a circular unit.) This satisfies the elegant formula

which establishes yet another explicit test of unique factorization: the equality c_d = ε_d is a “litmus” requirement for the unique factorization principle to hold in R_d.

To give the flavor of the formulas involved, let p be an odd prime number and let a be an integer not divisible by p. Then define σ_p (a) to be +1 if a is a quadratic residue modulo p, that is, if a is congruent to the square of an integer modulo p, and -1 if not. The simple trigonometric sums of (1) and (6) generalize to quadratic Gauss sums:

This formula is not too hard to prove, apart from determining which sign is correct in the initial ±, but after considerable efforts Gauss managed to work this out too. To see the connection between, say, formula (6) and (16) note that when p = 5, the left-hand side of (16) is and the right-hand side is

As for the circular unit c_p, it is defined to be

and this leads to further formulas. For example, when p = 5, we have ε_p = τ₅ = (1 + ), and since h₅ = 1, formula (6) for p = 5 tells us that

14 The Degree of an Algebraic Number

If Θ is an algebraic integer that is also a rational number, then Θ is an “ordinary” integer. Here is the proof of this fact. If Θ is a rational number, then we may write Θ = C/D as a fraction in lowest terms. If Θ is also an algebraic integer, then it is the root of a monic polynomial with rational integer coefficients, Θⁿ + a₁Θ^n-1 + ···+ a_n, so we have an equation

(C/D)ⁿ + a₁(C/D)^n-1 + ··· + a_n-1 (C/D) + a_n = 0.

Multiplying through by Dⁿ we get

Cⁿ + a₁C^n-1D + ··· + a_n-1CD^n-1 + a_nDⁿ = 0,

where all terms are (ordinary) integers, and all but the first one is divisible by D. If D > 1 then it has some prime factor p, so all terms apart from the first are also divisible by p. Since the terms add up to zero, it follows that p divides Cⁿ, which implies that p divides C, which contradicts the assertion that the fraction C/D is in its lowest terms. This in turn contradicts the hypothesis that O can be expressed as a ratio of whole numbers in the first place. As the reader may like to verify, this fact implies the result attributed to Theaetetus above, that is irrational if and only if A is not a perfect square.

The degree of an algebraic number Θ is defined to be the smallest degree, n, of any polynomial relation Θⁿ + a₁Θ^n-1 + ··· + a_n-1Θ + a_n = 0 that Θ satisfies, where the coefficients a_i are rational numbers. The corresponding polynomial, P(X) = Xⁿ + a₁Xⁿ-1 + ··· + a_n-1X + a_n is unique, since if there were two of them then their difference would be of smaller degree and would also have Θ as a root. (One could make it monic by dividing it through by the leading coefficient.) Let us call P(X) the minimal polynomial of Θ. The minimal polynomial is irreducible over the field of rational numbers: that is, it cannot be factored as a product of two polynomials, each of smaller degree and having rational numbers as coefficients. (If it could, then it would not be of minimal degree, since one of its factors would have Θ as a root.) The minimal polynomial P(X) of Θ is a factor of any monic polynomial G(X) with rational coefficients that has Θ as root. (The greatest common divisor of P and G is another monic polynomial with rational coefficients that has Θ as a root, so it cannot be of degree smaller than that of P and it must therefore be P.) The minimal polynomial P(X) of Θ has distinct roots. (If P(X) had multiple roots, then a little elementary calculus shows that it would share a nontrivial factor with its derivative, P´(X). Since the derivative is of lower degree than P(X) and again has rational coefficients, the greatest common divisor of P and P′ would provide a nontrivial factorization of P(X), contradicting its irreducibility.)

A fundamental result due to Gauss is that the nth root of unity ζ_n = e^2πi/n is an algebraic integer of degree precisely (n), where is Euler’s -function. For example, if p is prime, the minimal polynomial of ζ_p is

which is of degree (p) = p - 1.

15 Algebraic Numbers as Ciphers Determined by Their Minimal Polynomials

We have expressly insisted that our algebraic numbers are complex numbers (of a certain sort). But another possible attitude toward an algebraic number, Θ, an attitude at times promoted by Kronecker, among others, is to deal with Θ as an unknown satisfying only the algebraic relations implied by the fact that it is a root of its (unique monic) minimal polynomial with rational coefficients. For example, if the minimal polynomial of Θ is P(X) = X³ - X - 1, then, according to this view, Θ is just an algebraic symbol that comes with the rule that any occurrence of Θ³ may be replaced by Θ + 1 (rather as the complex number i can be regarded as a symbol with the property that i² may be replaced by -1). Any root of the minimal polynomial of O satisfies all the same polynomial relations with rational coefficients that Θ satisfies; these roots are called conjugates of Θ. If Θ is an algebraic number of degree n, then Θ has n distinct conjugates, all of them again, of course, algebraic numbers.

16 A Few Remarks about the Theory of Polynomials

Central to the theory of polynomials in one variable—and, therefore, particularly to the theory of algebraic numbers—is the general relationship that roots have to coefficients:

The polynomial A_j (T₁, T₂, . . . , T_n) is homogeneous of degree j (this means that every monomial in it has total degree j), has integer coefficients, and is symmetric in (i.e., unchanged by any permutation of) the variables T₁ T₂, ···, T_n

The constant term is given by the product of the roots:

A_n(T₁, T₂, . . . , T_n) = T₁ · T₂ ···· T_n,

which is known as the norm form. The coefficient of X^n-1 is given by the sum of the roots:

A₁(T₁, T₂, . . . , T_n) = T₁ · T₂ ···· T_n,

and this is the trace form.

When n = 2 the norm and trace are all the symmetric polynomials in the list. For n = 3, beyond the norm and trace we also have the symmetric polynomial of degree two:

It is of major importance to this theory, and more specifically to GALOIS THEORY [V.21], that the symmetry properties of the conjugate roots are nicely reflected in these symmetric polynomials. In particular, we have the fundamental result that any symmetric polynomial in T₁, T₂, . . . , T_n with rational coefficients can be expressed as a polynomial with rational coefficients in the symmetric polynomials A_j (T₁, T₂, . . . , T_n) and similarly with integral coefficients. For example, the equation above shows that can be expressed as

A₁(T₁, T_A2, T₃)² - 2A₂(T₁, T₂, T₃).

17 Fields of Algebraic Numbers and Rings of Algebraic Integers

The inverse of a nonzero algebraic number is again an algebraic number; the sum, difference, and product of two algebraic numbers are algebraic numbers; the sum, difference, and product of two algebraic integers are algebraic integers. The neat proofs of these (latter) facts are a good demonstration of the power of linear algebra, and in particular of Cramer’s rule. This states that any matrix with integer coefficients (and therefore also any linear transformation of a finite-dimensional vector space that preserves an integer lattice) satisfies a monic polynomial identity with integer coefficients.

To see just how useful this remark is for finding polynomial relations, and more specifically for showing that the collections of algebraic numbers and algebraic integers are closed under sums and products, try your hand at showing that + is an algebraic integer. One way to do it is to search for the monic fourth-degree polynomial equation that it satisfies. But this is hardly a beautiful calculation! If, however, you are familiar with linear algebra, then a less painful route is to form the four-dimensional vector space over the rational numbers, generated by 1, , , and (which are linearly independent when the scalars are rational). Multiplication by + defines a linear transformation T of this vector space, and one can compute its characteristic polynomial P. The Cayley-Hamilton theorem says that P(T) = 0, and this translates into the statement that + is a root of P.

These “closure properties” we have just discussed lead us to study, in complete generality, fields of algebraic numbers and rings of algebraic integers. A number field is a field that is generated (as a field) by finitely many algebraic numbers. A standard result tells us that any number field K can in fact be generated by a single carefully chosen algebraic number. The degree of this algebraic number equals the degree of K, which is defined to be the dimension of K when K is viewed as a vector space over the field of rational numbers. One of the main introductory observations of Galois theory is that if K is a number field of degree n, then there are exactly n distinct ring homomorphisms (“embed- dings”) t: K → from K into the field of complex numbers. (This means that t sends 1 to 1 and respects the addition and multiplication laws within K. That is, ι(x+ y) ι(x) + ι(y) and ι(x·y) = ι(x) · ι(y)·) From these embeddings, we can construct some very useful rational-valued functions on K. For any element x in K, we form the n complex numbers x₁, x₂, . . . , x_n that are the images of x under the n different embeddings of K into . We then let

a_j(x) = A_j(x₁,x₂, . . . , x_n),

where A_j(X₁,X₂, . . . , X_n) is the jth symmetric polynomial of section 14 above. (Because the polynomials A_j are symmetric, we do not have to worry about the order of the images x_l, x₂ , . . . , x_n in the above expression.) It is not immediately obvious that the values of a_j are rational numbers, but there is a theorem that tells us this.

If an algebraic number Θ in K generates K (as a field), then the rational numbers a_j(Θ) are the coefficients of its minimal polynomial; in general they are the coefficients of a power of its minimal polynomial. The most prominent of these functions are the multiplicative function a_n (x) = x_l · x₂ ···· x_n, called the norm function, usually denoted x N_K/(X), and the additive function a_l (x) = x₁+x₂ + ··· + x_n, called the trace function, usually denoted x trace_K/(x).

The trace function can be used to define a fundamental symmetric bilinear form on the -vector space K,

〈x,y〉 = trace_K/(x · y),

which turns out to be nondegenerate. This nondegeneracy, together with the fact that if x,y are both algebraic integers, then 〈x, y〉 is an ordinary integer, can be used to show that the ring (K) of a1l algebraic integers in K is finitely generated as an additive group. More specifically, there is a basis of algebraic integers in K, that is, a finite set {Θ1, Θ2 , . . . , Θ_n}, such that any other algebraic integer in K can be expressed as an “ordinary” integer combination of the numbers Θ_i.

Let us summarize this structure. The number field K is a finite-dimensional vector space over and comes equipped with a nondegenerate bilinear symmetric form (x,y) 〈x,y〉, and also with a lattice (K) ⊂ K. Moreover, the restriction of the bilinear form to (k) takes on integral values.

The discriminant of K, denoted D(k), is defined to be the DETERMINANT [III.15] of the matrix whose ij-entry is 〈Θ_i,Θ_j〉, for {Θ₁,Θ₂, . . . , Θ_n} a basis of the lattice (k); this determinant does not depend on the basis chosen.

The discriminant represents important information about the number field K. For one thing, there is a natural generalization to any number field of the notions of splitting and ramification that we discussed for quadratic fields, and the prime divisors p of D(K) are precisely those prime numbers that ramify in the field extension K. By a theorem of MI NKOWSKI [V1.64], the absolute value of the discriminant D(K) of a number field K of degree n is always greater than

This is greater than 1 unless K is the field of rational numbers. It follows that any nontrivial extension of the field of rational numbers has some prime that ramifies in it, a result that would be very hard to prove without the help of the algebraic structures we have just defined. This integer D(K) really is quite a discriminating “tag” for our number field K, for, by a theorem of HERMITS [VI.47], given any integer D there are only finitely many different number fields with discriminant equal to D. (Not all integers can be discriminants: as is true for quadratic number fields, the integers D that are discriminants are either divisible by 4 or else congruent to 1 modulo 4.)

18 On the Size(s) of the Absolute Values of All Conjugates of an Algebraic Integer

As we have just seen, the coefficients of the minimal polynomial for an algebraic integer Θ are given by the ordinary integers a_j (Θ₁, Θ₂, . . . , Θ_n), where the numbers Θ_i are all the conjugates of Θ. The sizes of all these coefficients must therefore all be less than some universal number M that depends only on the degree of and the largest absolute value of any of its conjugates. As a consequence, given any n and any positive number B, there are only finitely many algebraic integers Θ of degree less than n such that the absolute values of Θ and its conjugates are all less than B. (This is because for any n and M there are only finitely many polynomials of degree less than or equal ton with the absolute values of all their integer coefficients at most M.) This finiteness result is the key to the following observation, due to Kronecker: if Θ is an algebraic number and if the absolute values of Θ and of all of its conjugates are equal to 1, then Θ is a root of unity. Indeed, all the powers of Θ have degree at most that of Θ, and they enjoy the same property: their absolute value, and that of all their conjugates, is equal to 1. Consequently, there are only finitely many such algebraic numbers, from which it follows that there must be at least one coincidence of the form Θ^a = Θ^b for different a and b. But this can happen only if Θ is a root of unity.

19 Weil Numbers

To follow this thread for just a bit, let us generalize the hypothesis of Kronecker’s observation, and define a Weil number³ of absolute value r to be a nonzero algebraic integer such that it and all of its conjugates have the same absolute value r. By the discussion in the previous section there are only finitely many distinct Weil numbers of given degree and absolute value. By Kronecker’s theorem, which we have just described, the Weil numbers of absolute value 1 are precisely the roots of unity. Here are further basic facts that you might try to prove. First, the quadratic Weil numbers ω are precisely those quadratic algebraic integers such that |trace(ω)| , where ω’ is the (algebraic) conjugate of ω. Second, if p is prime then a quadratic Weil number ω of absolute value is a prime element of the (unique) ring of quadratic integers R_d that contains ω, and therefore gives a prime factorization ωω’ = ±p of the integer p in that ring.

Weil numbers of absolute value p^v/2, where p is again a prime number and v is a natural number, are extremely important in arithmetic: they hold the key to counting numbers of rational solutions of systems of polynomial equations over finite fields. For just one concrete example, the Gaussicn integer ω = -1 + i and its algebraic conjugate (which, in this instance, is also its complex conjugate) ϖ = -1 - i are Weil numbers (of absolute value 2) that control the number of solutions of the equation y² - y = x³ - x over all finite fields of size a power of 2. Specifically, the number of solutions of that equation over a field of order 2^v is given by the formula

2^v - (-1-i)^v - (-1+i)^v

(which is an ordinary integer). This leads to another immense chapter of mathematics.

20 Epilogue

The single symmetry α α’, the algebraic conjugation in the rings R_d that we have discussed, gave birth, thanks to ABEL [VI.33] and GALOIS [VI.41] in the beginning of the nineteenth century, to the rich study of (Galois) groups of symmetries of general number fields (see THE INSOLUBILITY OF THE QUINTIC [V.21]). This study continues with great intensity, since these Galois groups and their linear representations hold the key to a very detailed understanding of number fields. In its modern dress, algebraic number theory is closely connected with what is often called ARITHMETIC GEOMETRY [IV.5]. Kronecker’s dream of getting explicit control of a wealth of algebraic number theoretic material by expressing algebraic numbers in terms of natural analytic functions has not yet been fully realized. Nevertheless, the scope of this dream (and, one might also add, the supply of natural analytic and algebraic functions) has expanded substantially: the full range of algebraic geometry and group representation theory is now being brought to bear on it. This is done, for example, by the Langlands program, which among other things works with objects known as Shimurci varieties. On the one hand, these varieties have close connections with the theory of group representations and classical algebraic geometry, which greatly helps us to understand them. On the other hand, they are a rich source of concrete linear representations of Galois groups of number fields. This program, one of the glories of current mathematics, will, I expect, make a terrific chapter for a Companion to Mathematics to be written at the beginning of the next century.

Further Reading

Basic Texts

First, I list three classics that require a minimum of background.

Davenport, H. 1992. The Higher Arithmetic: An Introduction to the Theory of Numbers. Cambridge: Cambridge University Press.

Gauss, C. F. 1986. Disquisitiones Arithmeticae, English edn. New York: Springer.

Hardy, G. H., and E. M. Wright. 1980. An Introduction to the Theory of Numbers, 5th edn. Oxford: Oxford University Press.

At a more advanced level, the following are extraordinary expository books.

Borevich, Z. I., and I. R. Shafarevich. 1966. Number Theory. New York: Academic Press.

Cassels, J., and A. Fröhlich. 1967. Algebraic Number Theory. New York: Academic Press.

Cohen, H. 1993. A Course in Computational Algebraic Number Theory. New York: Springer.

Ireland, K., and M. Rosen. 1982. A Classical Introduction to Modern Number Theory, 2nd edn. New York: Springer.

Serre, J.-P. 1973. A Course in Arithmetic. New York: Springer.

Technical Articles and Books

Baker, A. 1971. Imaginary quadratic fields with class number 2. Annals of Mathematics (2) 94:139–52.

Brauer, R. 1950. On the Zeta-function of algebraic number fields. I. American Journal of Mathematics 69:243–50.

Brauer, R. 1950. On the Zeta-function of algebraic number fields. II. American Journal of Mathematics 72:739–46.

Goldfeld, D. 1985. Gauss’s class number problem for imaginary quadratic fields. Bulletin of the American Mathematical Society 13:23–37.

Granville, A., and G. Martin. 2006. Prime number races. American Mathematical Monthly 113:1–33.

Gross, B., and D. Zagier. 1986. Heegner points and derivatives of L-series. Inventiones Mathematicae 84:225–320.

Heegner, K. 1952. Diophantische Analysis and Modulfunktionen. Mathematische Zeitschrift 56:227–53.

Hua, L.-K. 1942. On the least solution of Pell’s equation. Bulletin of the American Mathematical Society 48:731–35.

Lang, S. 1970. Algebraic Number Theory. Reading, MA: Addison-Wesley.

Narkiewicz, W. 1973. Algebraic Numbers. Warsaw: Polish Scientific Publishers.

Siegel, C. L. 1935. Über die Classenzahl quadratischer Zahlörper. Acta Arithmetica 1:83–86.

Stark, H. 1967. A complete determination of the complex quadratic fields of class-number one. Michigan Mathematical Journal 14:1–27.

1. The continued-fraction expansion of any real quadratic algebraic number has an eventually recurring pattern in its entries, as is vividly exhibited by the two examples (2) and (7) given above.

2.BOMBELLI [V1.8], in the sixteenth century, would refer to irrational square roots, of positive or of negative numbers, as “deaf” (reminiscent of the word surd that is still in use) and as “numbers impossible to name.”

3. This is a weaker condition than is usually required for Weil numbers but our deviation from standard usage should not be the cause of too much confusion.