3.4 Graph-based Visual Saliency
An alternative approach is based on a parallel graph calculation model called graph-based visual saliency (GBVS) [6]. The first two steps of the GBVS model are similar to the original BS model that extracts low-level features from input image by various filters, but there are differences such as: (1) the centre–surround process in the alternation is omitted for orientation feature channels, as mentioned in Step 2 of Section 3.3.1; (2) for the contrast feature map of intensity channel, the luminance variance (centre–surround) is computed in a local neighbourhood of the same scale; (3) the number of scale is changed (for simplicity, only a few scales are considered); (4) Multiscale feature maps are rescaled to the same size with different resolutions. Notably, in the GBVS model, creating the feature maps does not need subtraction between the finer and coarser scales as in the BS (Equation 3.9a). The next steps of the GBVS model are to form the activation map from each feature map based on graph theory (i.e., by using the adjacency matrix of the graph and iterations of the Markov matrix), and normalizing of the activation map is also based on the Markov matrix, and the two steps are totally different from the original BS model.
3.4.1 Computation of the Activation Map
Suppose a feature map p (in the form of greyscale image) is given, 
, an activation map 
is driven from the adjacency matrix related to p, such that the activation map Ap has more saliency at the unusual regions in p. The adjacency matrix is built based on graph theory. Consider each pixel in the feature map p as a node of a graph. The weight between node (i, j) and node (k, l) is defined by
where 
is the dissimilarity of the values for the pair of nodes, which can be calculated from two possible approaches: one is Kullback-Leibler (KL) divergence mentioned in Section 2.6.2, and the other simply uses the absolute difference between 
and 
. The two approaches are shown in Equations 3.30a and (3.30b), respectively.
The function Ga (i − k), (j − l)) is a Gaussian function related to the distance between locations of node (
) and node (
):
where σ is a parameter that adapts the attenuation degree of function Ga with distance. From Equations 3.29, 3.30a, 3.31, the weight between a pair of nodes is proportional to their values' difference and inversely proportional to their distance. If m × n pixels in feature map p are set as nodes of a graph and the number of nodes 
, and the weight of each pair of nodes as the edge's weight of the graph, then an adjacency matrix of the graph with N × N elements is created. It is a symmetrical matrix with zero diagonal elements due to the zero value of the first term in Equation 3.29. If the weights at each column of the adjacency matrix are normalized (each outbound edge's weight is deemed to be the transition probability), then the adjacency matrix becomes a Markov matrix denoted as M. Now the Markov matrix is not a symmetrical matrix, and it represents a transition chain from a state at time (t − 1) to another state at t. Suppose that the initial 2D activation map is rewritten as a normalized vector (random or arbitrary normalized vector), 
, referred to as the state vector (or node vector), 
. The state vector will be transferred to the next state by the Markov matrix and the final equilibrium vector is the iterated results of the state vector:
It is known that the iterations of Equation 3.32 must be convergent according to the power method for computing the eigenvector of a matrix which corresponds to the maximum eigenvalue, if there is no other eigenvalue of the matrix that equals to the eigenvalue under consideration [32]. The convergent state vector, 
, is just the eigenvector of the Markov matrix M related to the maximal eigenvalue. Finally, the equilibrium state vector 
is recovered to the 2D map that is the activation map Ap for corresponding feature map 
.
Why can the activation map Ap enhance the salient objects or attentive regions in the feature map 
? Considering the initial state vector 
as a source vector and each element as a source (i.e., each node is a pool of source initially) and since these elements with higher values in M correspond to the paired nodes with higher dissimilarity and closer distance, with the iterations of Equation 3.32 the sources 
will flow into these nodes' pool with larger weights; in the other words, the sources have higher probabilities to flow into these nodes with larger weights. As a result, the concentrated places of higher dissimilar nodes have larger accumulation, which are often the location of objects or the focus of attention. The isolated noise in feature maps and similar regions cannot form a pool of massive nodes in state vector transitions, and it is therefore suppressed.
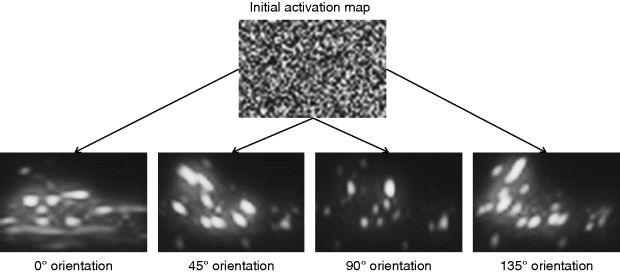
Figure 3.7 shows an image and its saliency map by using the GBVS method that is to simply combine five activation maps (four orientation maps and a luminance map) at only one scale, without normalization. It can be seen that the places with salient objects in the original image are prominent in the saliency map. Figure 3.8 is the initial random state vector (it is rewritten as a 2D form) and the convergent results of Equation 3.32 of Figure 3.7 by 30 iterations for four orientation activation maps. The Markov matrixes for the four different orientation features are different, so the resulting activation maps represent different orientation features, though the initial random state vector (2D form, source pool in each node) is the same because the Markov matrix can drive the sources into these close pool nodes with larger discrepancy. This is just coincident with the attention focus of humans.
Figure 3.7 An image and its saliency map. Reproduced from http://worldislandparadise.com/ (accessed November 25, 2012)
Figure 3.8 Convergent results of Equation 3.32 for four orientation activation maps
3.4.2 Normalization of the Activation Map
The initial state vector (source vector) is normalized, so the total sources' quantity is fixed (e.g., the summation of all the elements' value is one). In addition, each column of the Markov matrix is normalized too, and the element of each column of the Markov matrix represents the probability of a source flowing into another source pool in transition. Thereby the Markov transition does not change the total sources' quantity and only changes the distribution of the sources. The resultant activation map has been normalized: summation of all the pixels' values is one. However, for the purpose of further concentrating these nodes with enough sources and wiping away unimportant nodes, another Markov matrix is adopted to normalize each activation map. Suppose that an activation map Ap with m × n pixels is given, set each pixel of Ap as a node in the graph, and the weight of the edge between node (
) and node (
) for the adjacency matrix of Ap is defined as
where function Ga is the same as Equation 3.31, and Ap(k, l) is the grey-value at node (k, l) of the activation map. Notably, now the diagonal elements of the adjacency matrix are not equal to zero. With the same procedure as the computation of an activation map, each column of the adjacency matrix is normalized and the Markov matrix MN for normalization is created. After computing the equilibrium distribution over all nodes, the massive sources will flow into those nodes with high value in the activation map due to high wN[6]. The nodes with similar value in the activation map, after normalization, will not contribute to the final saliency map. Figure 3.9 shows the comparison of the BS model and the GBVS model. For the sake of fairness, in Figure 3.9, the BS model uses six feature maps for each of four orientation pyramids and one intensity pyramid in centre q = {2, 3, 4} and surround s = {3, 4} (30 feature maps in total), the GBVS model uses three resolutions (2, 3, 4) for the same orientation and intensity maps (15 feature maps in total), and normalization of Equation 3.33 is not adopted. Although the centre–surround operation in the BS model can pop out the edges of objects in the image, it may be unable to yield the objects' regions (extents) clearly – Figure 3.9(b). The GBVS model, by using Markov matrix iterations will group the dispersive edges into integral objects that stand out from their circumambience – Figure 3.9(c). The quantitative comparison of some experiments for matching the human eye movement data described in [6] also demonstrates that the GBVS model is better than the original BS model.
Figure 3.9 The comparison of the BS model and the GBVS model (a) original image (from http://www-sop.inria.fr/members/Neil.Bruce/eyetrackingdata.zip); (b) saliency map of the BS model; (c) saliency map of the GBVS model
As demonstrated, the GBVS model of combining computation of activation and normalization, both based on graph theory, improves the performance of the saliency map if the salient object regions/extents are meaningful in applications. Also, since its processing of feature maps does not need the centre–surround operation (as in the original BS model), the computational speed is fast, especially in hardware implementation, since the computation of all nodes in the GBVS model can be performed in parallel as in a neuron network. Although the GBVS model has a number of merits, its shortcoming is obvious because it needs to calculate two Markov matrices with the larger size (i.e., 
) and this requires big memory space when the size of input image is large. Similarly with the BS model, the GBVS model is easily programmable and its MATLAB® code is available at [33].