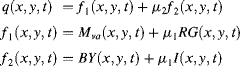4.4 Phase Spectrum of the Quaternion Fourier Transform Approach

In the case of multiple channels, PFT can be easily extended to a phase quaternion Fourier transform (PQFT) approach if multidimensional data at each pixel can be represented as a quaternion [5, 6]. The quaternion is a mathematical tool in multidimensional signal processing [28]. In later discussion, we will see that the use of the quaternion in the visual attention model has somewhat biological reason.

4.4.1 Biological Plausibility for Multichannel Representation

Most of the spatial domain models consider several low-level features as different feature maps or channels, which are coincident with physiological results. Let us recall the cells in the low-level visual cortex. Several simple cells that are close together share a receptive field in the input scene. These simple cells extract different features in the receptive field such as intensity, colour, orientations and so on, which can be simulated by a neural network [29]. Figure 4.7 gives a sketch of receptive fields and their related simple cells, where visual input is regarded as the input image or retina of the eye, and the ellipses on the visual input are these overlapped receptive fields that cover the whole visual input. Each receptive field is related to a cell set in a row-dashed block or to same location (one pixel) of many feature images. In Figure 4.7 we only draw the receptive fields on one side of the visual input. In each row-dashed block of this figure there are five cells that represent five different kinds of low-level features that share the same receptive field. It should be noted that the number of features is not fixed to five here. Figure 4.7 leads to two ways of representing multichannel signal processing in the brain. One is the same as spatial domain models that are based on separate features, and the other is based on the cells sharing the same receptive field. In the frequency domain, the two representations conduct two kinds of method.

Figure 4.7 Receptive fields and their related simple cells

In the former representation, we consider that the cells at the same location of all row line boxes extract the same feature from the visual input as shown in the right of Figure 4.7. For example, if the first cell in row line boxes is in charge of extracting the intensity feature, then all the first cells of the row line boxes will form a plane parallel to the visual input and construct an intensity feature image p_I. In this manner, several parallel feature maps can be regarded as several feature channels similar to the spatial domain model. For an input RGB (red-green-blue) colour image, the intensity feature at location (x, y) can be written as

(4.17)

where , and are three colours at pixel (x, y). Equation 4.17 is the same as Equation 3.1 in the BS model. In the same way, the second and third cells in all the row line boxes construct colour opponent feature images (channels) p_RG and p_BY and so on. The p_RG and p_BY can make use of broadly tuned colour as Equations 3.2, 3.3 or 3.4 in Chapter 3. The multichannel SR or PFT use this way to calculate a conspicuity map for each channel (p_I, p_RG and p_BY, etc.) by Fourier and inverse Fourier transform respectively, and then to sum the conspicuity maps of all the feature channels together, obtaining the final saliency map. Figures 4.4 and 4.6 are the results of using this representation to calculate the final saliency map.

However, the simple summation of these separate conspicuity maps is probably not reasonable. There is no evidence in physiological experiments to support the idea: the contribution of conspicuity map for each channel is equal. Especially, the normalization of the conspicuity map of each channel is actualized independently. An alternative representation considers the cells that share the same receptive field (the cells in the row-dashed block of Figure 4.7) as a unit, and all the computation is carried out for these units. The reason why it can do this is based on the premise that the simple operation of the PFT approach is very easy to extend the computation from scalar to multiple dimensions. In addition, there is a mathematical tool for multidimensional signal processing, called quaternion or hypercomplex number to represent these units. The algorithm based on units is the phase spectrum of quaternion Fourier transform (PQFT) already mentioned. In order to understand the PQFT algorithm, a brief introduction to quaternion follows.

4.4.2 Quaternion and Its Properties

Complex numbers have been widely applied to mathematics, physics and engineering because multiplication of complex numbers is achieved as a whole unit with a rule for the product of two numbers together. In 1843, Hamilton proposed a way for triple-number multiplication and created the quaternion [28]. Later, various works on mathematics introduced the algebra of the quaternion [30].

Definition A quaternion includes one real number and three imaginary numbers that can be represented as

(4.18)

where μ_i, i = 1, 2, 3 is the imaginary axis, a is the real part, Re(q) = a, b, c and d are the imaginary parts,

The quaternion has many properties and rules for calculation of itself that are discussed separately in other books. Here we only list some useful rules for the PQFT approach.

Properties

1. The index of imaginary axis μi, i = 1, 2, 3 satisfies

and

(4.19)

This means that the multiplication of the quaternion does not satisfy the commutative law.

2. The conjugate complex number of a quaternion can be written as . The norm or modulus of a quaternion is defined as

(4.20)

If the norm of a quaternion , then the quaternion is referred to as a unit quaternion. When the real part of a quaternion is equal to zero, we call it as pure quaternion,

3. Representation of the quaternion in polar coordinates: any quaternion can be written in polar coordinates as:

(4.21)

where and

In Equation 4.21, μ is a unit pure quaternion (its norm is equal to one), referred to as the eigenaxis of a quaternion, and ϕ denotes the eigenangle, which satisfies:

(4.22)

4. Given two quaternions and their addition and subtraction rules can be defined as

(4.23)

5. Given two quaternions, q₁ and q_2, according to Equation 4.19, the product of quaternions q₁ and q₂ is

(4.24)

Note that here , since the quaternion product fails to obey the commutative law.

6. Quaternions and hypercomplex numbers

A quaternion can be rewritten in Cayley–Dickson form [31] or symplectic decomposition:

(4.25)

where A and B are two complex numbers and . Therefore, the quaternion can be regarded as a complex number of two complex numbers called hypercomplex numbers. It can simultaneously process four data in a unit. This idea is easy to extend to eight data in a unit (biquaternion), if A and B are quaternions, and , and in Equation 4.25 changes to . It is clear that the biquaternion [32] includes one real number and seven imaginary numbers projected on axes, and all μ_i, i = 1, 2, 3, . . . 7 are orthogonal to each other. The quaternion has been successfully applied to colour image processing when the triple colour values (red-green-blue) of a pixel are represented by a pure quaternion [33–37]. It does not have to process each colour channel independently, but instead it treats all colour components as a triple data in a whole unit, and it can achieve high accuracy.

From above properties of quaternions and the structure of visual signal processing in the low-level cortex of the brain (Figure 4.7), it is easy to set the cells in the row-dashed block (the local features) as a quaternion if the number of cells is equal or less than four. For the case of more than four features, we make use of biquaternion or high- dimensional hypercomplex number as an entire unit to calculate the saliency map in the frequency domain.

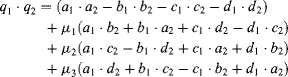
4.4.3 Phase Spectrum of Quaternion Fourier Transform (PQFT)

We will now extend the PFT approach in a single channel to multiple channels by using quaternions. As with the PFT, the PQFT model has four steps: (1) quaternion representation of the input image, that constructs a quaternion image: the data on each pixel of the input image are represented as a quaternion that consists of colour, intensity and motion features. When the motion feature is included in the quaternion, the PQFT can obtain a spatiotemporal saliency map; (2) perform a quaternion Fourier transform for the quaternion image and compute its modulus and eigenangle of each quaternion spectral component; (3) set the modulus for all frequency components to unity and maintain their eigenangles, and then recover the image from the frequency domain to the spatial domain by inverse quaternion Fourier transform; (4) post-process the recovered image by using a low-pass Gaussian filter and get the spatiotemporal saliency map. The detailed analysis and equations are shown as follows.

1. Quaternion representation of input image

If the input frame in a colour video at time t is defined as I_F(x, y, t), t = 1, 2, . . . N_I, where N_I is the total number of frames, then and will be the red, green and blue feature at pixel (x, y) of time t in frame I_F. Four broadly tuned colour channels are created by Equation 4.26 that is similar with Equation 3.2 for the BS model in Chapter 3 adopted from [2].

(4.26)

Note that all broadly turned colours in Equation 4.46 are positive (negative value is set to zero). The two-colour opponent components of red/green and blue/yellow for the given location (x, y) at time t are

(4.27)

(4.28)

The intensity and motion features at location (x, y) of time t are calculated by Equations 4.29 and 4.30:

(4.29)

(4.30)

where τ is the latency coefficient and M_va is the absolute motion feature in [5, 6]. It may be better to use the relative motion feature (mentioned in Section 3.2 of Chapter 3) instead of absolute motion if global motion exists between two frames. Now there are four features like the four cells in the row-dashed block, so the unit feature at location (x, y) at time t is described as a quaternion.

(4.31)

According to property (6) of the quaternion in Section 4.4.2, can be represented in Cayley–Dickson form or in symplectic decomposition as

(4.32)

where each part, and can be represented as a complex image. We call the simplex part and the perplex part. Equation 4.32 is easy to transfer to Equation 4.31, using .

2. Quaternion Fourier transform (QFT) for the quaternion frame

The quaternion Fourier transform was proposed in 1992 by Ell [38] and has since had a lot of applications to colour image processing [37, 39–41]. By using the Cayley–Dickson form (Equation 4.32), the QFT of a frame at time t can be implemented in two complex Fourier transforms – the simplex part and perplex parts. If the transform results for the two parts are and respectively, the quaternion frequency located at (u, v) will be expressed as

(4.33)

To avoid confusion in two complex Fourier transforms, the Cayley–Dickson form is constructed as an equivalent complex form:

(4.34)

The difference of equivalent complex number in Equation 4.34 from the f_i, i = 1, 2 in Equation 4.32 is that the imaginary axis μ₁ is replaced by j, and real components of each complex number are rewritten as . The following Fourier transform is for the equivalent complex number , in which j is regarded as a constant.

(4.35)

Equation 4.35 is isomorphic to the standard complex 2D Fourier transform with imaginary index μ₁, and they can be implemented by existing FFT code, where (x, y) is the location of each pixel in the 2D spatial domain and (u, v) is the frequency component in the frequency domain. M and N are the numbers of pixel in width and height, respectively. It is worth noting that the computational results of the exponential term to the left and to the right of the equivalent complex number are different in the quaternion Fourier transform due to the property of quaternion multiplication. Here, in 4.35, we only use the left mode. Thus, the inverse quaternion Fourier transform should also be left mode, which is obtained from Equation 4.35 by changing the sign of the exponential and summing over u and v instead of x and y. The inverse transform can be expressed as follows:

(4.36)

Now let us show how to process the spectrum in the frequency domain after FFT (Equation 4.35). Since the imaginary axis j in the Fourier transform is constant, the results of Equation 4.35 can be described as

(4.37)

It is noticed that the spectrum and are complex numbers on imaginary axis μ₁. Now we substitute μ₁ for j in Equation 4.37 and obtain the spectral component located at (u, v) for simplex and perplex parts.

(4.38)

When substituting Equation 4.38 into Equation 4.33, the spectral component located at (u, v) is still a quaternion.

(4.39)

According the property (3) of quaternion, the quaternion spectral component located at (u, v) can be written in polar form

(4.40)

There are three quantities: modulus, phase and the eigenaxis μ (a unit pure quaternion), that is defined in property (3) of Section 4.4.2.

3. Inverse quaternion Fourier transform

Let modulus or neglect the modulus while keeping the phase spectrum for Equation 4.40, and then reconstruct the quaternion spectral components in rectangular coordinates according to property (3) of Section 4.3.2. The inverse Fourier transform is similar to the Fourier transform in the spatial domain (step 2). First, the quaternion spectral components in rectangular coordinates have to be rewritten in Cayley–Dickson form in simplex and perplex parts ( and ), and then the Cayley–Dickson form is constructed in the equivalent complex form (employing j as the imagery axis of each part). We carry out an inverse complex Fourier transform to the equivalent complex form by using Equation 4.36 and substitute μ₁ for j. Finally the recovered quaternion located at (x, y) in the spatial domain is shown as follows.

(4.41)

The recovered quaternion image in the spatial domain is

4. Calculate the saliency map at each location (x, y) and time t

(4.42)

where is the value of a 2D low-pass Gaussian filter (σ = 8) at location (x, y), and are weights for each channel. Setting w_i = 1, Equation 4.42 can be expressed as

(4.43)

where G is 2D Gaussian filter. It is obvious that the PQFT has the same steps as the PFT, in which the steps for both approaches can be stated as applying fast Fourier transforms (FFT), setting the modulus to one (keeping the phase spectrum), taking the inverse FFT, and post-processing for enhancement on the saliency map. However, for PQFT, we need to construct the quaternion, and all the processes are based on the quaternion; contrarily, PFT is utilized in separate channels for multivariate data.

Since the PQFT does not need to fix the resolution of the input frame, it can generate the spatiotemporal saliency map under different resolutions just like the human visual system. While observers see a frame or image in a very short interval or an observer views the image or frame from a distance, the resolution of the saliency map will be low, because the detailed local features will be suppressed. Contrarily, the long-term view or the close view produces detailed saliency. PQFT can adopt different resolutions to suit different cases [6].

Apparently, saliency maps at different resolutions are not alike. In spatial domain models (the BS model and its variations), the pyramid includes all possible resolutions. However, the PQFT considers hierarchical selectivity, that is to shift attention from the parent object to its child group or a single object [6]. For example, a white boat is drifting in blue lake, and some people with different colour clothes are sitting on the boat. If an observer glances at the lake (in the case of low resolution), he will first look the boat as the salient object (parent object), since the white boat pops out from blue lake. If the observer takes more time to look at the scene (mid resolution), the group of persons in the boat may be regarded as the salient object (child object). In long-time observation (high resolution), each person in the boat can be perceived as a salient object to pop out. The resolution selection is achieved by filtering and down-sampling the input frame and the variable sizes of processed image or video frame representing different resolutions. Since the size of the saliency map is less than the input frame, a smaller size of saliency map denotes a coarser resolution. The hierarchical selection of resolution of the PQFT has been used in multiresolution image coding [6].

Although PQFT requires quaternion image as its input data, its calculation is still very fast. Also, it is easy to implement because the code of the quaternion Fourier transform is available in [42]. This book has a Companion Website (www.wiley.com/go/zhang/visual) that includes PFT, PQFT and other frequency domain models in MATLAB® codes.

4.4.4 Results Comparison

The computational cost of PQFT is mainly due to the quaternion Fourier transform. As stated in [43], PQFT's computational complexity is based on the real multiplication process and can be expressed as 4MN·log₂MN if the input image has M × N pixels. Considering the other aspects causing computational cost such as building the quaternion, changing the quaternion to Cayley–Dickson form and the equivalent complex numbers, transferring the frequency components into polar form and so on, the cost of PQFT is slightly higher than PFT and SR. However, it can still meet the requirements for real-time applications. To compare the PQFT model with other computational models fairly, five computational models (two spatial domain models and three frequency models), and two different types of test dataset, used in [6] and [2, 3], are selected. One of them is a video of 15 frames per second which consists of 988 frames with a resolution of 640 × 480 pixels. And the other one is a dataset of 100 natural images with the resolution around 800 × 600 pixels. For the still images from the dataset of natural scenes, the real part of the quaternion is set to zero in the PQFT model since there is no information for motion in still images. The testing results based on the average computation time showed that PQFT is third among the five models. Table 4.2 demonstrates the average time cost (seconds) per frame or image for the two testing sets. It is worth noting that the original BS model (NVT) is implemented in C++ and other four models are coded by MATLAB® [6].

Table 4.2 Average time cost per frame in test video and per image in natural image set [6]. © 2010 IEEE. Reprinted, with permission, from C. Guo, L. Zhang, ‘A Novel Multiresolution Spatiotemporal Saliency Detection Model and its Applications in Image and Video Compression’, IEEE Transactions on Image Processing, Jan. 2010.

The computational attention models in the frequency domain are faster than those in the spatial domain (see Table 4.2). The PFT model is the fastest and the SR model takes the second. PQFT in the MATLAB® version still meets real-world (16–17 f/s) notwithstanding its third rank. Although the BS model with C++ code is the fastest among the spatial domain models, its processing time is only around 2–3 f/s which is slower than the frequency-based approaches in average regarding the overall datasets.

The results of performance comparison among the five computational models in [6] showed that the PQFT model is better than the other four models for the two testing sets. Since a quantitative index is not involved now, which will be discussed in Chapter 6, we only give the following three intuitive examples (psychological pattern, the pattern with repeating texture and a man-made object image of a city) in order to compare PQFT and the other frequency models (SR and PFT).

Example 4.1 Psychological pattern

In the top left of Figure 4.8 (the original pattern) a horizontal red bar (the target) is located among the many heterogeneous vertical red bars (distractors). All three frequency models (PQFT, PFT and SR) can pop out the target (the top row of Figure 4.8) in their saliency maps. Although in the PQFT model the target does not stand out from the distractors, the detection result for the region of interest is still satisfactory. However, the original psychological pattern in the bottom left of Figure 4.8 is a red inclined bar (target) among many heterogeneous inclined green bars (distractors), and also some distractors may have the same or similar orientation as the target. Even in these conditions, PQFT can highlight the target. On the other hand, PFT and SR fail in their saliency map, as shown in the bottom row of Figure 4.8. This is because PQFT considers all features as a whole, while PFT and SR process their features separately, which may lose some information.

Example 4.2 Pattern with repeating texture

As mentioned above, the SR model cannot suppress the repeating texture that expresses the peaks in the amplitude spectrum, but these peaks are just redundancy in the scene. Figure 4.9(a) illustrates an array of vertical bars with an absent location. The human can rapidly find the absent location as the salient object. Both PQFT and PFT can detect the location in their saliency map as the human does (Figures 4.9(b) and (c)), but SR fails in this case since the locations with vertical bars and the location without a bar are all enhanced in their saliency. The absent location cannot be detected by the SR model.

Figure 4.8 Saliency maps of three frequency models for two psychological patterns (where the psychological patterns are from http://ilab.usc.edu/imbibes). Reproduced with permission from Laurent Itti, ‘iLab Image Databases,’ University of Southern California, http://ilab.usc.edu/imgdbs (accessed October 1, 2012)

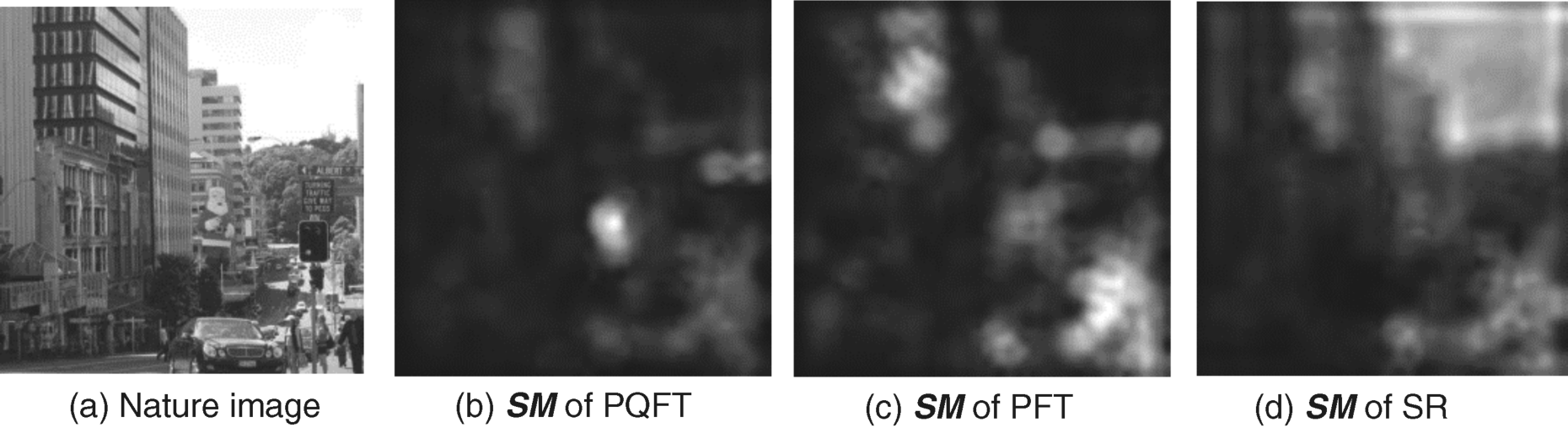
Example 4.3 Image of a city scene

Figure 4.10(a) displays the black and white version of a colour city image in which a striking statue of Father Christmas dressed in red stands up near several high buildings. In general, people first shift their focus to the statue of Father Christmas. The saliency map of the PQFT model gives the same focus (Figure 4.10(b)). However, PFT and SR lose the important object since the reflected light of the glass curtain wall on the high building or the bright sky are enhanced in the separately processed intensity channel and the colour channels, and their saliency maps give prominence to these unimportant areas (Figure 4.10(c) and (d)).

Figure 4.9 Saliency maps of three frequency models for pattern (64 × 64 pixels) with repeating texture

Figure 4.10 Saliency maps of three frequency models for a natural image within a city scene

4.4.5 Dynamic Saliency Detection of PQFT

In PQFT the motion feature represented by the real part of the quaternion only considers the difference between two successive frames. That is, only absolute motion is considered as introduced in Section 3.2. However, since motion features often include background motion such as camera motion, absolute motion in Equation 4.30 is not helpful in some cases. In the frequency domain, background motion can be separated by utilizing phase correlation [44], which provides the motion vector for translational motion. Let I_c and I_p be the current and previous intensity frames, and F_c and F_p be their Fourier transform, respectively. The equation to calculate the phase correlation of successive frames is

(4.44)

where is the inverse Fourier transform, () denotes global motion (background motion) between the successive frames and is the conjugate complex of F_p. The phase difference of two spectra denotes the global displacement. Given () by computing Equation 4.44, the two successive frames are shifted by the global motion to compensate for the camera motion. The new motion feature in the quaternion is the difference between the shifted frames. A qualitative comparison of the simple difference frame and the difference frame with motion compensated is shown in Figure 4.11.

Figure 4.11 Comparison of PQFT without and with motion compensation. (a) motion frame with moving pedestrians; (b) difference frame with camera shake; (c) compensated difference frame; (d) saliency map of motion channel of (b); (e) saliency map of motion channel of (c) [45]. With kind permission from Springer Science + Business Media: Lecture Notes in Computer Science, ‘Biological Plausibility of Spectral Domain Approach for Spatiotemporal Visual Saliency’, 5506, © 2009, 251–258, Peng Bian and Liming Zhang

It is obvious that the saliency map of the compensated difference frame is better at popping out moving pedestrians. The phase correlation method (Equation 4.44) can also be used in other frequency domain models such as PFT, SR and the models introduced in the following sections of this chapter.

In summary, PQFT, as with PFT, sets the amplitude spectrum to a constant (one) while keeping the phase spectrum in the frequency domain, implements the inverse Fourier transform and post-processes the recovered image in the spatial domain to finally obtain its saliency map. The difference is that PQFT is based on a quaternion image; that is all the features in each pixel of the image are combined in a quaternion. This kind of whole processing method is similar to the structure of the primary visual cortex in the brain. The mathematical tool and properties of quaternion give PQFT better performance than PFT or SR. However, the quaternion may suffer from its computational complexity. Its computational speed is five times slower than PFT. Even so, PQFT is still a good choice in many engineering applications because it can meet the real-time processing requirement for image coding or robot vision.