Arbitrage Pricing: Continuous-State, Continuous-Time Models

SERGIO M. FOCARDI, PhD

Partner, The Intertek Group

FRANK J. FABOZZI, PhD, CFA, CPA

Professor of Finance, EDHEC Business School

In this entry, we describe arbitrage pricing in the continuous-state, continuous-time setting. There are a number of important conceptual changes in going from a discrete-state, discrete-time setting (as described in the entry “Arbitrage Pricing: Finite-State Models”) to a continuous-state, continuous-time setting. First, each state of the world has probability zero. This precludes the use of standard conditional probabilities for the definition of conditional expectation and requires the use of filtrations (rather than of information structures) to describe the propagation of information. Second, the tools of matrix algebra are inadequate; the more complex tools of calculus and stochastic calculus are required. Third, simple generalizations are rarely possible as many pathological cases appear in connection with infinite sets.

THE ARBITRAGE PRINCIPLE IN CONTINUOUS TIME

Let's start with the definition of basic concepts. The economy is represented by a probability space where is the set of possible states, is the σ-algebra of events, and P is a probability measure. Time is a continuous variable in the interval . The propagation of information is represented by a filtration . The latter is a family of -algebras such that .

Each security i is characterized by a payoff-rate process and by a price process . In this continuous-state setting, and are real variables with a continuous range such that and are, respectively, the payoff-rate and the priceof the i-th asset at time and in state . Note that represents a rate of payoff and not a payoff as was the case in the discrete-time setting. The payoff-rate process must be interpreted in the sense that the cumulative payoff of each individual asset is

We assume that the number of assets is finite. We can therefore use the vector notation to indicate a set of processes. For example, we write and to indicate the vector process of payoff rates and prices respectively. All payoff-rates and prices are stochastic processes adapted to the filtration . One can make assumptions about the price and the payoff-rate processes. For example, it can be assumed that price and payoff-rate processes satisfy a set of stochastic differential equations or that they exhibit finite jumps. Later in this entry we will explore a number of these processes.

Conditional expectations are defined as partial averaging. In fact, given a variable , its conditional expectation is defined as a variable that is -measurable and whose average on each set is the same as that of X:

for and is -measurable.

The law of iterated expectations applies as in the finite-state case:

In a continuous-state setting, conditional expectations are variables that assume constant values on the sets of infinite partitions. Imagine the evolution of a variable X. At the initial date, identifies the entire space . At each subsequent date t, the space is partitioned into an infinite number of sets, each determined by one of the infinite values of .1 However, these sets have measure zero. In fact, they are sets of the type: determined by specific values of the variable Xt. These sets have probability zero as there is an infinite number of values Xt. As a consequence, we cannot define conditional expectation as expectation under the usual definition of conditional probabilities the same way we did in the case of finite-state setting.

Trading Strategies and Trading Gains

We have to define the meaning of trading strategies in the continuous-state, continuous-time setting; this requires the notion of continuous trading. Mathematically, continuous trading means that the composition of portfolios changes continuously at every instant and that these changes are associated with trading gains or losses. A trading strategy is a (vector-valued) process such that is the portfolio held at time t. To ensure that there is no anticipation of information, each trading strategy θ must be an adapted process.

Given a trading strategy, we have to define the gains or losses associated with it. In discrete time, the trading gains equal the sum of payoffs plus the change of a portfolio's value

over a finite interval .

We must define trading gains when time is a continuous variable. It is not possible to replace finite sums of stochastic increments with pathwise Riemann-Stieltjes integrals after letting the time interval go to zero. The reason is that, though we can assume that paths are continuous, we cannot assume that they have bounded variation. As a consequence, pathwise Riemann-Stieltjes integrals generally do not exist. However, we can assume that paths are of bounded quadratic variation. Under this latter assumption, using Itô isometry, we can define pathwise Itô integrals and stochastic integrals.

Let's first assume that the payoff-rate process is zero, so that there are only price processes. Under this assumption, the trading gain Tt of a trading strategy can be represented by a stochastic integral:

In the rest of this section, we will not strictly adhere to the vector notation when there is no risk of confusion. For example, we will write to represent the scalar product S. If a payoff-rate process is associated with each asset, we have to add the gains consequent to the payoff-rate process. We therefore define the gain process

as the sum of the price processes plus the cumulative payoff-rate processes, and we define the trading gains as the stochastic integral

How can we match the abstract notion of a stochastic integral with the buying and selling of assets? In discrete time, trading gains have a meaning that is in agreement with the practical notion of buying a portfolio of assets, holding it for a period, and then selling it at market prices, thus realizing either a gain or a loss. One might object that in continuous time this meaning is lost. How can a process where prices change so that their total variation is unbounded be a reasonable representation of financial reality? This is a question of methodology that is relevant to every field of science. In classical physics, the use of continuous models was assumed to reflect reality; time and space, for example, were considered continuous. Quantum physics upset the conceptual cart of classical physics, and the reality of continuous processes has since been questioned at every level. In quantum physics, a theory is considered to be nothing but a model useful as a mathematical device to predict measurements. This is, in essence, the theory set forth in the by Niels Bohr and the school of Copenhagen; it has now become mainstream methodology in physics. It is also, ultimately, the point of view of positive economics. In a famous and widely quoted essay, Milton Friedman (1953) wrote:

The relevant question to ask about the “assumptions” of a theory is not whether they are descriptively “realistic,” for they never are, but whether they are sufficiently good approximations for the purpose in hand. And this question can be answered only by seeing whether the theory works, which means if it yields sufficiently accurate predictions.

In the spirit of positive economics, continuous-time financial models are mathematical devices used to predict, albeit in a probabilistic sense, financial observations made at discrete intervals of time. Stochastic gains predict trading gains only at discrete intervals of time–the only intervals that can be observed. Continuous-time finance should be seen as a logical construction that meets observations only at a finite number of dates, not as a realistic description of financial trading.

Let's consider processes without any intermediate payoff. A self-financing trading strategy is a trading strategy such that the following relationships hold:

We first define arbitrage in the absence of a payoff-rate process. An arbitrage is a self-financing trading strategy such that: and , or and . If there is a payoff-rate process, a self-financing trading strategy is a trading strategy such that the following relationships hold:

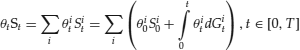
where is the gain process as previously defined. An arbitrage is a self-financing trading strategy such that: and , or and .

ARBITRAGE PRICING IN CONTINUOUS-STATE, CONTINUOUS-TIME

The abstract principles of arbitrage pricing are the same in a discrete-state, discrete-time setting as in a continuous-state, continuous-time setting. Arbitrage pricing is relative pricing. In the absence of arbitrage, the price and payoff-rate processes of a set of basic assets fix the prices of other assets given the payoff-rate process of the latter. If markets are complete, every price process can be computed in this way. In a discrete-state, discrete-time setting, the computation of arbitrage pricing is done with matrix algebra. In fact, in the absence of arbitrage, every price process can be expressed in two alternative ways:

1. Prices are equal to the normalized conditional expectation of payoffs deflated with state prices under the real probabilities:

2. Prices are equal to the conditional expectation of discounted payoffs under the risk-neutral probabilities

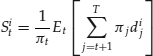
State-price deflators and risk-neutral probabilities can be computed solving systems of linear equations for a kernel of basic assets. The above relationships are algebraic linear equations that fix all price processes.

In a continuous-state, continuous-time setting, the principle of arbitrage pricing is the same. In the absence of arbitrage, given a number of basic price and payoff stochastic processes, other processes are fixed. The latter are called redundant securities as they are not necessary to fix prices. If markets are complete, every price process can be fixed in this way. In order to make computations feasible, some additional assumptions are made, in particular, all payoff-rate and price processes are assumed to be Itô processes.

The theory of arbitrage pricing in a continuous-state, continuous-time setting uses the same tools as in a discrete-state, discrete-time setting. Under an equivalent martingale measure, all price processes become martingales. Therefore prices can be determined as discounted present value relationships. Equivalent martingale measures are the same concept as state-price deflators: After appropriate deflation, all processes become martingales. The key point of arbitrage pricing theory is that both equivalent martingale measures and state-price deflators can be determined from a subset of the market. All other processes are redundant.

In the following sections we will develop the theory of arbitrage pricing in steps. First, we will illustrate the principles of arbitrage pricing in the case of options, arriving at the Black-Scholes option pricing formula. We will then extend this theory to more general derivative securities. Subsequently, we will state arbitrage pricing theory in the context of equivalent martingale measures and of state-price deflators.

OPTION PRICING

We will now apply the concepts of arbitrage pricing to option pricing in a continuous-state, continuous-time setting. Suppose that a market consists of three assets: a risk-free asset (which allows risk-free borrowing and lending at the risk-free rate of interest), a stock, and a European option. We will show that the price processes of a stock and of a risk-free asset fix the price process of an option on that stock.

Suppose the risk-free rate is a constant r. The value Vt of a risk-free asset with constant rate r evolves according to the deterministic differential equation of continually compounding interest rates:

The above is a differential equation with separable variables. After separating the variables, the equation can be written as

which admits the solution where V0 is the initial value of the bank account. This formula can also be interpreted as the price process of a risk-free bond with deterministic rate .

Stock Price Processes

Let's now examine the price process of the stock. Consider the process where Bt is a standard Brownian motion. From the definition of Itô integrals, it can be seen that this process, which is called an arithmetic Brownian motion, is the solution of the following diffusion equation:

where is a constant called the drift of the diffusion and σ is a constant called the volatility of the diffusion.

Consider now the process . Applying Itô's lemma it is easy to see that this process, which is called a geometric Brownian motion, is an Itô process that satisfies the following stochastic differential equation:

where x is an initial value, and Bt is a standard Brownian motion. We assume that the stock price process follows a geometric Brownian motion and that there is no payoff-rate process.

Now consider a European call option, which gives the owner the right but not the obligation to buy the underlying stock at the exercise price K at the expiry date T. Call the price of the option at time t. The price of the option as a function of the stock price is known at the final expiry date. If the option is rationally exercised, the final value of the option is

In fact, the option can be rationally exercised only if the price of the stock exceeds K. In that case, the owner of the option can buy the underlying stock at the price K, sell it immediately at the current price St and make a profit equal to . If the stock price is below K, the option is clearly worthless. After T, the option ceases to exist.

How can we compute the option price at every other date? We can arrive at the solution in two different but equivalent ways: (1) through hedging arguments and (2) the equivalent martingale measures. In the following sections we will introduce hedging arguments and equivalent martingale measures.

Hedging

To hedge means to protect against an adverse movement. The seller of an option is subject to a liability as, from his point of view, the option has a negative payoff in some states. In our context, hedging this option means to form a self-financing trading strategy formed with the stock plus the risk-free asset in appropriate proportions such that the option plus this hedging portfolio is risk free. Hedging the option implies that the hedging portfolio perfectly replicates the option payoff in every possible state.

A European call option has only one payoff at the expiry date. It therefore suffices that the hedging portfolio replicates the option payoff at that date. Suppose that there is a self-financing trading strategy in the bond and the stock such that

To avoid arbitrage, the price of the option at any moment must be equal to the value of the hedging self-financing trading strategy. In fact, suppose that at any time the self-financing strategy has a value lower than the option:

An investor could then sell the option for , make an investment in the trading strategy, and at time T liquidate both the option and the trading strategy. As the final liquidation has value zero in every state of the world, so that the initial profit is a risk-free profit. A similar reasoning could be applied if, at any time , the strategy had a value higher than the option. Therefore, we can conclude that if there is a self-financing trading strategy that replicates the option's payoff, the value of the strategy must coincide with the option's price at every instant prior to the expiry date.

Observe that the above reasoning is an instance of the law of one price. If two portfolios have the same payoffs at every moment and in every state of the world, their price must be the same. In particular, if a trading strategy has the same payoffs of an asset, its value must coincide with the price of that asset.

The Black-Scholes Option Pricing Formula

Let's now see how the price of the option can be computed. Assume that the price of the option is a function of time and of the price of the underlying stock: . This assumption is reasonable but needs to be justified; for the moment it is only a hint as to how to proceed with the calculations. It will be justified later by verifying that the pricing formula produces the correct final payoff.

As St is assumed to be an Itô process, in particular a geometric Brownian motion, —which is a function of St—is an Itô process as well. Therefore, using Itô's formula, we can write down the stochastic equation that must satisfy. Itô's formula prescribes that:

Suppose now that there is a self-financing trading strategy . We can write this equation as

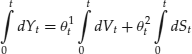
or, in differential form, as

If the trading strategy replicates the option price process, the two expressions for ---the one obtained through Itô's lemma and the other obtained through the assumption that there is a replicating self-financing trading strategy—must be equal:

The equality of these two expressions implies the equality of the coefficients in and respectively. Equating the coefficients in yields

As , substituting, we obtain

We have now obtained the self-financing trading strategy in function of the stock and option prices. Substituting and equating the coefficients of yields

Simplifying and eliminating common terms, we obtain

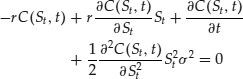
If the function satisfies this relationship, then the coefficients in match. The above relationship is a partial differential equation (PDE). This equation can be solved with suitable boundary conditions. Boundary conditions are provided by the payoff of the option at the expiry date:

The closed-form solution of the above PDE with the above boundary conditions was derived by Black and Scholes (1973) and referred to as the Black-Scholes option pricing formula:

with

and where is the cumulative normal distribution.

Let's stop for a moment and review the logical steps we have followed thus far. First, we defined a market made by a stock whose price process follows a geometric Brownian motion and a bond whose price process is a deterministic exponential. We introduced into this market a European call option. We then made two assumptions: (1) The option's price process is a deterministic function of the stock price process; and (2) the option's price process can be replicated by a self-financing trading strategy.

If the above assumptions are true, we can write a stochastic differential equation for the option's price process in two different ways: (1) Using Itô's lemma, we can write the option price stochastic process as a function of the stock stochastic process; and (2) using the assumption that there is a replicating trading strategy, we can write the option price stochastic process as the stochastic process of the trading strategy. As the two equations describe the same process, they must coincide. Equating the coefficients in the deterministic and stochastic terms, we can determine the trading strategy and write a deterministic PDE that the pricing function of the option must satisfy. The latter PDE together with the boundary conditions provided by the known value of the option at the expiry date uniquely determine the option pricing function.

Note that the above is neither a demonstration that there is an option pricing function, nor a demonstration that there is a replicating trading strategy. However, if both a pricing function and a replicating trading strategy exist, the above process allows one to determine both by solving a partial differential equation. After determining a solution to the PDE, one can verify if it provides a pricing function and if it allows the creation of a self-financing trading strategy. Ultimately, the justification of the existence of an option's pricing function and of a replicating self-financing trading strategy resides in the possibility of actually determining both. Absence of arbitrage ensures that this solution is unique.

Generalizing the Pricing of European Options

We can now generalize the above pricing methodology to a generic European option and to more general price processes for the bond and for the underlying stock. In the most general case, the process underlying a derivative need not be a stock price process. However, we suppose that the underlying is a stock price process so that replicating portfolios can be formed. We generalize in three ways:

• The option's payoff is an arbitrary finite-variance random variable.
• The stock price process is an Itô process.
• The short-rate process is stochastic.

Following the definition given in the finite-state setting, we define a European option on some underlying process St as an asset whose payoff at time T is given by the random variable where is a continuous real-valued function. In other words, a European option is defined as a security whose payoff is determined at a given expiry date T as a function of some underlying random variable. The option has a zero payoff at every other date . This definition clearly distinguishes European options from American options, which yield payoffs at random stopping times.

Let's now generalize the price process of the underlying stock. We represent the underlying stock price process as a generic Itô process. A generic univariate Itô process can be represented through the differential stochastic equation:

where x is the initial condition, B is a standard Brownian motion, and and are given functions ) . The geometric Brownian motion is a particular example of an Itô process.

Let's now define the bond price process. We retain the risk-free nature of the bond but let the interest rate be stochastic. Recall that in a discrete-state, discrete-time setting, a bond was defined as a process that, at each time step, exhibits the same return for each state though the return can be different in different time steps. Consequently, in continuous-time we define a bond price process as the following integral:

where r is a given function that represents the stochastic rate. In fact, the rate r depends on the time t and on the stock price process St. Application of Itô's lemma shows that the bond price process satisfies the following equation:

We can now use the same reasoning that led to the Black-Scholes formula. Suppose that there are both an option pricing function and a replicating self-financing trading strategy

We can now write a stochastic differential equation for the process in two ways:

• Applying Itô's lemma to
• Directly to

The first approach yields

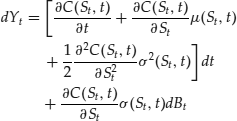
The second approach yields

Equating coefficients in we obtain the trading strategy

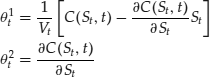
and the PDE

with the boundary conditions . Solving this equation we obtain a candidate option pricing function. In each specific case, one can then verify that the option pricing function effectively solves the option pricing problem.

STATE-PRICE DEFLATORS

We now extend the concepts of state prices and equivalent martingale measures to a continuous-state, continuous-time setting. As in the previous sections, the economy is represented by a probability space where is the set of possible states, is the σ-algebra of events, and P is a probability measure. Time is a continuous variable in the interval . The propagation of information is represented by a filtration . A multivariate standard Brownian motion in RD adapted to the filtration is defined over this probability space. We know that there are mathematical subtleties that we will not take into consideration, as regards whether (1) the filtration is given and the Brownian motion is adapted to the filtration or (2) the filtration is generated by the Brownian motion.

Suppose that there are N price processes that form a multivariate Itô process in . Trading strategies are adapted processes that represent the quantity of each asset held at each instant. In order to ensure the existence of stochastic integrals, we require the processes and any trading strategy to be of bounded variation. Let's first suppose that there is no payoff-rate process. This assumption will be relaxed in a later section. Suppose also that one of these processes, say , is defined by a short-rate process r, so that

or

where rt is a deterministic function of t called the short-rate process. Note that could be replaced by a trading strategy. We can think of rt as the risk-free short-term continuously compounding interest rate and of as a risk-free continuously compounding bank account.

The concept of arbitrage and of trading strategy was defined in the previous section. We now introduce the concept of deflators in a continuous-time continuous-state setting. Any strictly positive Itô process is called a deflator. Given a deflator we can deflate any process X, obtaining a new deflated process

For example, any stock price process of a nondefaulting firm or the risk-free bank account is a deflator. For technical reasons it is necessary to introduce the concept of regular deflators. A regular deflator is a deflator that, after deflation, leaves unchanged the set of admissible bounded-variation trading strategies.

We can make the first step towards defining a theory of pricing based on equivalent martingale measures. It can be demonstrated that if is a regular deflator, a trading strategy is self-financing with respect to the price process if and only if it is self-financing with respect to the deflated price process

In addition, it can be demonstrated that the price process admits no arbitrage if and only if the deflated price process

admits no arbitrage.

A state-price deflator is a deflator with the property that the deflated price process is a martingale. A martingale is a stochastic process Mt such that its current value equals the conditional expectation of the process at any future time: . For each price process , the following relationship therefore holds:

This definition is the equivalent in continuous time of the definition of a state-price deflator in discrete time. In fact, a state-price deflator is defined as a process such that

If there is no intermediate payoff, as in our present case, the previous relationship can be written as

The next proposition states that if there is a regular state-price deflator, then there is no arbitrage. The demonstration of this proposition hinges on the fact that, as the deflated price process is a martingale, the following relationship holds:

and therefore any self-financing trading strategy is a martingale. We can thus write

If

which shows that there cannot be any arbitrage.

We have now stated that the existence of state-price deflators ensures the absence of arbitrage. The converse of this statement in a continuous-state, continuous-time setting is more delicate and will be dealt with later. We will now move on to equivalent martingale measures.

EQUIVALENT MARTINGALE MEASURES

In the previous section we saw that if there is a regular state-price deflator then there is no arbitrage. A state-price deflator transforms every price process and every self-financing trading strategy into a martingale. We will now see that, after discounting by an appropriate process, price processes become martingales through a transformation of the real probability measure into an equivalent martingale measure.2 This theory parallels the theory of equivalent martingale measures developed in the discrete-state, discrete-time setting in the entry “Arbitrage Pricing: Finite-State Models.” First some definitions must be discussed.

Given a probability measure P, the probability measure Q is said to be equivalent to P if both assign probability zero to the same events, that is, if if and only if for every event A. The equivalent probability measure Q is said to be an equivalent martingale measure for the process X if X is a martingale with respect to Q and if the Radon-Nikodym derivative

has finite variance. The definition of the Radon-Nikodym derivative is the same here as it is in the finite-state context. The Radon-Nikodym derivative is a random variable such that for every event A where IA is the indicator function of the event A.

To develop an intuition for this definition, consider that any stochastic process X is a time-dependent random variable Xt. The latter is a family of functions from the set of states to the real numbers indexed with time such that the sets are events for any real x. Given the probability measure P, the finite-dimension distributions of the process X are determined. The equivalent measure Q determines another set of finite-dimension distributions. However, the correspondence between the process paths and the states remains unchanged.

The requirement that P and Q are equivalent is necessary to ensure that the process is effectively the same under the two measures. There is no assurance that given an arbitrary process an equivalent martingale measure exists. Let's assume that an equivalent martingale measure does exist for the N-dimensional price process . It can be demonstrated that if the price process admits an equivalent martingale measure, then there is no arbitrage.

The proof is similar to that for state-price deflators as discussed above. Under the equivalent martingale measure Q, which we assume exists, every price process and every self-financing trading strategy becomes a martingale. Using the same reasoning as above it is easy to see that there is no arbitrage.

This result can be generalized; here is how. If there is a regular deflator such that the deflated price process admits an equivalent martingale measure, then there is no arbitrage. The proof hinges on the result established in the previous section that, if there is a regular deflator , the price process X admits no arbitrage if and only if the deflated price process admits no arbitrage.

Note that none of these results is constructive. They only state that the existence of an equivalent martingale measure with respect to a price process ensures the absence of arbitrage. Conditions to ensure the existence of an equivalent martingale measure with respect to a price process are given in the next section.

EQUIVALENT MARTINGALE MEASURES AND GIRSANOV'S THEOREM

We first need to establish an important mathematical result known as Girsanov's theorem. This theorem applies to Itô processes. Let's first state Girsanov's theorem in simple cases. Let X be a single-valued Itô process where B is a single-valued standard Brownian motion:

Suppose that a process and a process θ such that are given. Suppose, in addition, that the process θ satisfies the Novikov condition which requires

Then, there is a probability measure Q equivalent to P such that the following integral

defines a standard Brownian motion in R on with the same standard filtration of the original Brownian motion Bt. In addition, under Q the process X becomes

Girsanov's theorem states that we can add drift to a standard Brownian motion and still obtain a standard Brownian motion under another probability measure. In addition, by changing the probability measure we can arbitrarily change the drift of an Itô process.

The same theorem can be stated in multiple dimensions. Let X be an N-valued Itô process:

In this process, is an N-vector process and is an matrix. Suppose that there are both a vector process and a vector process such that where the product is not a scalar product but is performed component by component. Suppose, in addition, that the process θ satisfies the Novikov condition:

Then there is a probability measure Q equivalent to P such that the following integral

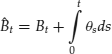
defines a standard Brownian motion in RD on with the same standard filtration of the original Brownian motion Bt. In addition, under Q the process X becomes

Girsanov's theorem essentially states that under technical conditions (the Novikov condition) by changing the probability measure, it is possible to transform an Itô process into another Itô process with arbitrary drift. Prima facie, this result might seem unreasonable. In the end the drift of a process seems to be a fundamental feature of the process as it defines, for example, the average of the process. Consider, however, that a stochastic process can be thought as the set of all its possible paths. In the case of an Itô process, we can identify the process with the set of all continuous and square integrable functions. As observed above, the drift is an average, and it is determined by the probability measure on which the process is defined. Therefore, it should not be surprising that by changing the probability measure it is possible to change the drift.

The Diffusion Invariance Principle

Note that Girsanov's theorem requires neither that the process X be a martingale nor that Q be an equivalent martingale measure. If X is indeed a martingale under Q, an implication of Girsanov's theorem is the diffusion invariance principle, which can be stated as follows. Let X be an Itô process:

If X is a martingale with respect to an equivalent probability measure Q, then there is a standard Brownian motion in under Q such that

Let's now apply the previous results to a price process where

and

If the short-term rate r is bounded, is a regular deflator. Consider the deflated processes:

By Itô's lemma, this process satisfies the following stochastic equation:

Suppose there is an equivalent martingale measure Q. Under the equivalent martingale measure Q, the discounted price process

is a martingale. In addition, by the diffusion invariance principle there is a standard Brownian motion in RD under Q such that:

Applying Itô's lemma, given that , we obtain the fundamental result:

This result states that, under the equivalent martingale measure, all price processes become Itô processes with the same drift.

Application of Girsanov's Theorem to Black-Scholes Option Pricing Formula

To illustrate Girsanov's theorem, let's see how the Black-Scholes option pricing formula can be obtained from an equivalent martingale measure. In the previous setting, let's assume that is a constant and

with σ constant. Let S be the stock price process and C be the option price process. The option's price at time T is

In this setting, therefore, the following three equations hold:

Given that is a martingale, we can write

It can be demonstrated by direct computation that the above formula is equal to the Black-Scholes option pricing formula presented earlier in this entry.

EQUIVALENT MARTINGALE MEASURES AND COMPLETE MARKETS

In the continuous-state, continuous-time setting, a market is said to be complete if any finite-variance random variable can be obtained as the terminal value at time T of a self-financing trading strategy . A fundamental theorem of arbitrage pricing states that, in the absence of arbitrage, a market is complete if and only if there is a unique equivalent martingale measure. This condition can be made more specific given that the market is populated with assets that follow Itô processes. Suppose that the price process is where, as in the previous section:

and is a standard Brownian motion in RD.

It can be demonstrated that markets are complete if and only if rank(σ) almost everywhere. This condition should be compared with the conditions for completeness we established in the discrete-state setting. In that setting, we demonstrated that markets are complete if and only if the number of linearly independent price processes is equal to the maximum number of branches leaving a node. In fact, market completeness is equivalent to the possibility of solving a linear system with as many equations as branches leaving each node.

In the present continuous-state setting, there are infinite states and so we need different types of considerations. Roughly speaking, each price process (which is an Itô process) depends on D independent sources of uncertainty as we assume that the standard Brownian motion is D-dimensional. In a finite-state setting this means that, if processes are Markovian, at each time step any process can jump to D different values. The market is complete if there are D independent price processes. Note that the number D is arbitrary.

EQUIVALENT MARTINGALE MEASURES AND STATE PRICES

We will now show that equivalent martingale measures and state prices are the same concept. We use the same setting as in the previous sections. Suppose that Q is an equivalent martingale measure after deflation by the process

where r is a bounded short-rate process. The density process for Q is defined as

where

is the Radon-Nikodym derivative of Q with respect to P. As in the discrete-state setting, the Radon-Nikodym derivative of Q with respect to P is a random variable

with average value on the entire space equal to 1 and such that, for every event A, the probability of A under Q is the average of :

It can be demonstrated that, given any -measurable random variable , the density process for Q has the following property:

To gain an intuition for the Radon-Nikodym derivative in a continuous-state setting, let's assume that the probability space is the real line equipped with the Borel σ-algebra and with a probability measure P. In this case, and we can write

or, . Given any random variable X with density f under P and density q under Q, we can then write

In other words, the random variable is a function that multiplies the density f to yield the density q.

We can now show the following key result. Given an equivalent martingale measure with density process a state-price deflator is given by the process

Conversely, given a state-price deflator , the density process

defines an equivalent martingale measure. In fact, suppose that Q is an equivalent martingale measure for with where

Then, using the above relationship we can write:

which shows that is a state-price deflator. The same reasoning in reverse order demonstrates that if is astate-price deflator then:

is a density process for Q.

ARBITRAGE PRICING WITH A PAYOFF RATE

In the analysis thus far, we assumed that there is no intermediate payoff. The owner of an asset makes a profit or aloss due only to the changes in value of the asset. Let's now introduce a payoff-rate process for each asset i. The payoff-rate process must be interpreted in the sense that the cumulative payoff of each individual asset is

We define a gain process

By the linearity of the Itô integrals, we can write any trading strategy as

If there is a payoff-rate process, a self-financing trading strategy is a trading strategy such that the following relationship holds:

An arbitrage is, as before, a self-financing trading strategy such that

The previous arguments extend to this case. An equivalent martingale measure for the pair is defined as an equivalent probability measure Q such that the Radon-Nikodym derivative

has finite variance and the process is a martingale. Under these conditions, the following relationship holds:

IMPLICATIONS OF THE ABSENCE OF ARBITRAGE

We saw that the existence of an equivalent martingale measure or of state-price deflators implies absence of arbitrage. We have also seen that, in the absence of arbitrage, markets are complete if and only if there is a unique equivalent martingale measure.

In a discrete-state, discrete-time context we could establish the complete equivalence between the existence of state-price deflators, equivalent martingale measures and absence of arbitrage, in the sense that any of these conditions implies the other two. In addition, the existence of a unique equivalent martingale measure implies absence of arbitrage and market completeness.

In the present continuous-state context, however, absence of arbitrage implies the existence of an equivalent martingale measure and of state price deflators only under rather restrictive and complex technical conditions. If we want to relax these conditions, the condition of absence of arbitrage has to be slightly modified. These discussions are quite technical and will not be presented in this entry.3

WORKING WITH EQUIVALENT MARTINGALE MEASURES

The concepts established in the preceding sections of this entry might seem very complex, abstract, and scarcely useful. On the contrary, they entail important simplifications in the computation of derivative prices. Applications of these computations can be found in the pricing of bonds and credit derivatives. Here we want to make a few general comments on how these tools are used.

The key result of the arbitrage pricing theory is that, under the equivalent martingale measure, all discounted price processes become martingales and all price processes have the same drift. Therefore, all calculations can be performed under the assumption that the change to an equivalent martingale measure has been made. This environment allows important simplifications. For example, as we have seen, the option pricing problem becomes a problem of computing the present value of simpler processes.

Obviously one has to go back to a real environment at the end of the pricing exercise. This is essentially a calibration problem, as risk-neutral probabilities have to be estimated from real probabilities. Despite this complication, the equivalent martingale methodology has proved to be an important tool in derivative pricing.

KEY POINTS

• A trading strategy is a vector-valued process that represents portfolio weights at each moment.
• Trading gains are defined as stochastic integrals.
• A self-financing trading strategy is one whose value at every moment is the initial value plus the trading gains at that moment.
• An arbitrage is a self-financing trading strategy whose initial value is either negative and the final value nonnegative or the initial value non-negative and the final value positive.
• The Black-Scholes option pricing formula can be established by replicating self-financing trading strategies.
• The Black-Scholes pricing argument is based on constructing a self-financing trading strategy that replicates the option price in each state and for each time.
• Absence of arbitrage implies that a replicating self-financing trading strategy must have the same price as the option.
• The Black-Scholes option pricing formula is obtained by solving the partial differential equation implied by the equality of the replicating self-financing trading strategy and the option price process.
• A deflator is any strictly positive Itô process; a state-price deflator is a deflator with the property that the deflated price process is a martingale.
• If there is a (regular) state-price deflator, then there is no arbitrage; the converse is true only under a number of technical conditions.
• Two probability measures are said to be equivalent if they assign probability zero to the same event.
• Given a process X on a probability space with probability measure P, the probability measure Q is said to be an equivalent martingale measure if it is equivalent to P and X is a martingale with respect to Q (plus other conditions).
• If there is a regular deflator such that the deflated price process admits an equivalent martingale measure, then there is no arbitrage.
• Under the equivalent martingale measure, all Itô price processes have the same drift.
• In the absence of arbitrage, a market is complete if and only if there is a unique equivalent martingale measure.

NOTES

1. One can visualize this process as a tree structure with an infinite number of branches and an infinite number of branching points. However, as the number of branches and of branching points is a continuum, intuition might be misleading.

2. The theory of equivalent martingale measures was developed in Harrison and Pliska (1981, 1985) and Harrison and Kreps (1979).

3. See Delbaen and Schachermayer (1994, 1999).

REFERENCES

Black, B., and Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–654.

Friedman, M. (1953). Essays in the Theory of Positive Economics. Chicago: University of Chicago Press.

Delbaen, F., and Schachermayer, W. (1994). A general version of the fundamental theorem of asset pricing. Mathematische Annalen 300 (3): 463–520.

Delbaen, F., and Schachermayer, W. (1999). The fundamental theorem of asset pricing for unbounded stochastic processes. Mathematische Annalen 312 (2): 215–250.

Harrison, J. M., and Kreps, D. M. (1979). Martingales and arbitrage in multiperiod securities markets. Journal of Economic Theory 20: 381–408.

Harrison, J. M., and Pliska, S. R. (1981). Martingales and stochastic integrals in the theory of continuous trading. Stochastic Process Application 11: 215–260.

Harrison, J. M., and Pliska, S. R. (1985). A stochastic calculus model of continuous trading: Complete markets. Stochastic Process Application 15: 313–316.