Risk Measures and Portfolio Selection
Most of the concepts in theoretical and empirical finance that have been developed over the last 50 years rest upon the assumption that the return or price distribution for financial assets follow a normal distribution. Yet, with rare exception, studies that have investigated the validity of this assumption since the 1960s fail to find support for the normal distribution. Moreover, there is mple empirical evidence that many—if not most—financial return series are heavy-tailed and, possibly, skewed. The “tails” of the distribution are where the extreme values occur. Empirical distributions for stock prices and returns have found that the extreme values are more likely than would be predicted by the normal distribution. This means that between periods where the market exhibits relatively modest changes in prices and returns, there will be periods where there are changes that are much higher (that is, crashes and booms) than predicted by the normal distribution. This is not only of concern to financial theorists, but also to practitioners seeking, for example, to produce probability estimates for financial risk assessment. To more effectively implement portfolio selection, alternative risk measures are needed.
In this entry, we review alternative risk measures that can be employed in portfolio selection, which can accommodate non-normal return distributions. These risk measures are classified as dispersion measures and safety-first measures. We begin with a discussion of the desirable features of investment risk measures.
DESIRABLE FEATURES OF INVESTMENT RISK MEASURES
In portfolio theory, the variance of a portfolio's return has been historically the most commonly used measure of investment risk. However, different investors adopt different investment strategies in seeking to realize their investment objectives. Consequently, intuitively, it is difficult to believe that investors have come to accept only one definition of risk. Regulators of financial institutions and commentators to risk measures proposed by regulators have proffered alternative definitions of risk. As noted by Dowd (2002, p. 1):
The theory and practice of risk management—and, included with that, risk measurement—have developed enormously since the pioneering work of Harry Markowitz in the 1950s. The theory has developed to the point where risk management/measurement is now regarded as a distinct sub-field of the theory of finance. …
Szegö (2004, p. 1) categorizes risk measures as one of the three major revolutions in finance and places the start of that revolution in 1997. The other two major revolutions are mean-variance analysis (1952–1956) and continuous-time models (1969–1973). He notes that alternative risk measures have been accepted by practitioners but “rejected by the academic establishment and, so far discarded by regulators!” (Szegö, 2004, p. 4).
Basic Features of Investment Risk Measures
Balzer (2001) argues that a risk measure is investor specific and, therefore, there is “no single universally acceptable risk measure.” He suggests several features that an investment risk measure should capture. Here we describe the following three features:
- Relativity of risk
- Multidimensionality of risk
- Asymmetry of risk
The relativity of risk means that risk should be related to performing worse than some alternative investment or benchmark. Balzer (1994, 2001) and Sortino and Satchell (2001), among others, have proposed that investment risk might be measured by the probability of the investment return falling below a specified risk benchmark. The risk benchmark might itself be a random variable, such as a liability benchmark (e.g., an insurance product), the inflation rate or possibly inflation plus some safety margin, the risk-free rate of return, the bottom percentile of return, a sector index return, a budgeted return, or other alternative investments. Each benchmark can be justified in relation to the goal of the portfolio manager. Should performance fall below the benchmark, there could be major adverse consequences for the portfolio manager.
In addition, the same investor could have multiple objectives and, hence, multiple risk benchmarks. Thus, risk is also a multidimensional phenomenon. However, an appropriate choice of the benchmarks is necessary in order to avoid an incorrect evaluation of opportunities available to investors. For example, too often, little recognition is given to liability targets. This is the major factor contributing to the underfunding of U.S. corporate pension sponsors of defined benefit plans.1
Intuition suggests that risk is an asymmetric concept related to the downside outcomes, and any realistic risk measure has to value and consider upside and downside differently. The standard deviation considers the positive and the negative deviations from the mean as a potential risk. In this case overperformance relative to the mean is penalized just as much as underperformance.
Intertemporal Dependence and Correlation with Other Sources of Risk
The standard deviation is a measure of dispersion and it cannot always be used as a measure of risk. The preferred investment does not always present better returns than the other. It could happen that the worst investment presents the greatest return in some periods. Hence, time could influence the investor's choices.
Clearly, if the degree of uncertainty changes over time, the risk has to change during the time as well. In this case, the investment return process is not stationary; that is, we cannot assume that returns maintain their distribution unvaried in the course of time. In much of the research published, stationary and independent realizations are assumed. The latter assumption implies that history has no impact on the future. More concrete, the distribution of tomorrow's return is the same independent of whether the biggest stock market crash ever recorded took place yesterday or yesterday's return equaled 10%.
As a result, the oldest observations have the same weight in our decisions as the most recent ones. Is this assumption realistic? Recent studies on investment return processes have shown that historical realizations are not independent and present a clustering of the volatility effect (time-varying volatility). Those phenomena lead to the fundamental time-series model autoregressive conditional heteroscedascity (ARCH) formulated by Engle (1981). In particular, the last observations have a greater impact in investment decisions than the oldest ones. Thus, any realistic measure of risk changes and evolves over time taking into consideration the heteroscedastic (time-varying volatility) behavior of historical series. An examination of the returns of say the equity return indexes such as the S&P 500 over some time period would show a propagation effect on another equity market, say the DAX 30. When we observe the highest peaks in one return index series, for example, there is an analogous peak in the other return index series. This propagation effect is known as cointegration of the return series, introduced by the fundamental work of Granger (1981) and elaborated upon further by Engle and Granger (1987). The propagation effect in this case is a consequence of the globalization of financial markets—the risk of a country/sector is linked to the risk of the other countries/sectors. Therefore, it could be important to limit the propagation effect by diverstfying the risk. As a matter of fact, it is largely proven that the diversification, opportunely modeled, diminishes the probability of big losses. Hence, an adequate risk measure values and models correctly the correlation among different investments, sectors, and markets.
ALTERNATIVE RISK MEASURES FOR PORTFOLIO SELECTION
The goal of portfolio selection is the construction of portfolios that maximize expected returns consistent with individually acceptable levels of risk. Using both historical data and investor expectations of future returns, portfolio selection uses modeling techniques to quantify “expected portfolio returns” and “acceptable levels of portfolio risk,” and provides methods to select an optimal portfolio.
It would not be an overstatement to say that modern portfolio theory as developed by Harry Markowitz (1952, 1959) has revolutionized the world of investment management. Allowing managers to appreciate that the investment risk and expected return of a portfolio can be quantified has provided the scientific and objective complement to the subjective art of investment management. More importantly, whereas previously the focus of portfolio management used to be the risk of individual assets, the theory of portfolio selection has shifted the focus to the risk of the entire portfolio. This theory shows that it is possible to combine risky assets and produce a portfolio whose expected return reflects its components, but with considerably lower risk. In other words, it is possible to construct a portfolio whose risk is smaller than the sum of all its individual parts.
Though practitioners realized that the risks of individual assets were related, prior to modern portfolio theory they were unable to formalize how combining them into a portfolio impacted the risk at the entire portfolio level or how the addition of a new asset would change the return/risk characteristics of the portfolio. This is because practitioners were unable to quantify the returns and risks of their investments. Furthermore, in the context of the entire portfolio, they were also unable to formalize the interaction of the returns and risks across asset classes and individual assets. The failure to quantify these important measures and formalize these important relationships made the goal of constructing an optimal portfolio highly subjective and provided no insight into the return investors could expect and the risk they were undertaking. The other drawback, before the advent of the theory of portfolio selection and asset pricing theory, was that there was no measurement tool available to investors for judging the performance of their investment managers.
The theory of portfolio selection set forth by Markowitz was based on the assumption that asset returns are normally distributed. As a result, Markowitz suggested that the appropriate risk measure is the variance of the portfolio's return and portfolio selection involved only two parameters of the asset return distribution: mean and variance. Hence, the approach to portfolio selection he proposed is popularly referred to as mean-variance analysis.
Markowitz recognized that an alternative to the variance is the semivariance.2 The semivariance is similar to the variance except that, in the calculation, no consideration is given to returns above the expected return. Portfolio selection could be recast in terms of mean-semivariance. However, if the return distribution is symmetric, Markowitz (1959, p. 190) notes that “an analysis based on (expected return) and (standard deviation) would consider these … (assets) as equally desirable.” He rejected the semivariance noting that the variance “is superior with respect to cost, convenience, and familiarity” and when the asset return distribution is symmetric, either measure “will produce the same set of efficient portfolios.” (Markowitz 1959, pp. 193–194).
There is a heated debate on risk measures used for valuing and optimizing the investor's risk portfolio. In this section and the one to follow, we describe the various portfolio risk measures proposed in the literature and more carefully look at the properties of portfolio risk measures.
According to the literature on portfolio theory, two disjointed categories of risk measures can be defined: dispersion measures and safety-first risk measures. In the remainder of this entry, we review some of the most well-known dispersion measures and safety-first measures along with their properties.3
In the following, we consider a portfolio of N assets whose individual returns are given by r1, … , rN. The relative weights of the portfolio are denoted as x1, … xn and, therefore, the portfolio return rp can be expressed as
![]()
We also provide a sample version of the discussed risk measures. The sample version will be based on a sample of length T of independent and identically distributed observations ![]()
![]() , k − 1, … , T of the portfolio return rp. These observations can be obtained from a corresponding sample of the individual assets.
, k − 1, … , T of the portfolio return rp. These observations can be obtained from a corresponding sample of the individual assets.
DISPERSION MEASURES
Several portfolio mean dispersion approaches have been proposed in the last few decades. The most significant ones are discussed below, and we provide for each measure an example to illustrate the calculation.
Mean Standard Deviation
In the mean standard deviation approach the dispersion measure is the standard deviation of the portfolio return rp (see Markowitz, 1959, and Tobin, 1958):
(1) ![]()
The standard deviation is a special case of the mean absolute moment discussed below. The sample version can be obtained from the general case by setting p = 2.
Mean Absolute Deviation
In the mean absolute deviation (MAD) approach, the dispersion measure is based on the absolution deviations from the mean rather than the squared deviations as in the case of the standard deviation.4 The MAD is more robust with respect to outliers. The MAD for the portfolio return rp is defined as
(2) ![]()
Mean Absolute Moment
The mean absolute moment (MAM(q)) approach is the logical generalization of the MQ approach. Under this approach the dispersion measure is defined as
Note that the mean absolute moment for q = 2 coincides with the standard deviation and for q = 1 the mean absolute moment reduces to the mean absolute deviation. One possible sample version of (3) is given by

where
![]()
denotes the sample mean of the portfolio return.
Gini Index of Dissimilarity
The index of dissimilarity is based on the measure introduced by Gini (1912, 1921).5 Gini objected to the use of the variance or the MAD because they measure deviations of individuals from the individual observations of the mean or location of a distribution. Consequently, these measures linked location with variability, two properties that Gini argued were distinct and do not depend on each other. He then proposed the pairwise deviations between all observations as a measure of dispersion, which is now referred to as the Gini measure.
While this measure has been used for the past 80 years as a measure of social and economic conditions, its interest as a measure of risk in the theory of portfolio selection is relatively recent. Interest in a Gini-type risk measure has been fostered by Rachev (1991) and Rachev and Gamrowski (1995). Mathematically, the Gini risk measure for the random portfolio return rp is defined as
where the minimum is taken over all joint distributions of (rp, rb) with fixed marginal distribution functions F and G:
![]()
Here rb is the benchmark return, say, the return of a market index, or just the risk-free rate (U.S. Treasury rate or LIBOR, for example). Expression (4) can be represented as the mean absolute deviation between the two distribution functions F and G:
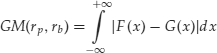
Given a sample or a distributional assumption for the benchmark return rb, the latter expression can be used for estimating the Gini index by calculating the area between the graphs of the empirical distribution function of rp and the (empirical) distribution function of rb.
Mean Entropy
In the mean entropy (M-entropy) approach, the dispersion measure is the exponential entropy. Exponential entropy is a dispersion measure only for portfolios with continuous return distribution because the definition of entropy for discrete random variables is formally different and does not satisfy the properties of the dispersion measures (positive and positively homogeneous). The concept of entropy was introduced in the last century in the classical theory of thermodynamics. Roughly speaking, it represents the average uncertainty in a random variable.
Probably its most important application in finance is to derive the probability density function of the asset underlying an option on the basis of the information that some option prices provide.6 Entropy was used also in portfolio theory by Philippatos and Wilson (1972) and Philippatos and Gressis (1975) and is defined as
![]()
where f is the density of the portfolio return. Thus, the exponential entropy is given by
(5) ![]()
The valuation of entropy can be done either by considering the empirical density of a portfolio or assuming that portfolio returns belong to a given family of continuous distributions and estimate their unknown parameters.
Mean Colog
In the mean colog (M-colog) approach, the dispersion measure is the covariance between the random variable and its logarithm.7 That is, the colog of a portfolio return is defined as
(6) ![]()
Colog can easily be estimated based on a sample of the portfolio return distribution by:

where
![]()
denotes the sample mean of the logarithm of one plus the portfolio return.
SAFETY-FIRST RISK MEASURES
Many researchers have suggested the safety-first rules as a criterion for decision making under uncertainty.8 In these models, a subsistence, a benchmark, or a disaster level of returns is identified. The objective is the maximization of the probability that the returns are above the benchmark. Thus, most of the safety-first risk measures proposed in the literature are linked to the benchmark-based approach.
Even if there are not apparent connections between the expected utility approach and a more appealing benchmark-based approach, Castagnoli and LiCalzi (1996) have proven that the expected utility can be reinterpreted in terms of the probability that the return is above a given benchmark. Hence, when it is assumed that investors maximize their expected utility, it is implicitly assumed that investors minimize the probability of the investment return falling below a specified risk benchmark.
Although it is not always simple to identify the underlying benchmark, expected utility theory partially justifies the using of the benchmark-based approach. Moreover, it is possible to prove that the two approaches are in many cases equivalent even if the economic reasons and justifications are different.9
Some of the most well-known safety-first risk measures proposed in the literature are described in the next section.
Classical Safety First
In the classical safety-first portfolio choice problem the risk measure is the probability of loss or, more generally, the probability ![]() of portfolio return less than λ. Generally, safety-first investors have to solve a complex, mixed integer linear programming problem to find the optimal portfolios. However, when short sales are allowed and return distributions are elliptical, depending on a dispersion matrix Q and a vector mean μ, then there exists a closed-form solution to the investor's portfolio selection problem:
of portfolio return less than λ. Generally, safety-first investors have to solve a complex, mixed integer linear programming problem to find the optimal portfolios. However, when short sales are allowed and return distributions are elliptical, depending on a dispersion matrix Q and a vector mean μ, then there exists a closed-form solution to the investor's portfolio selection problem:
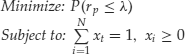
The interesting property of this optimization problem is that we are able to express the set of optimal portfolios explicitly as a function of the shortfall barrier λ, the mean vector μ, and the dispersion matrix Q. The mean m and the dispersion σ2 of these optimal portfolios can again be expressed as a function of the threshold λ, the mean vector μ, and the dispersion matrix Q. In the case where the elliptical family has finite variance (as, for example, the normal distribution), then the dispersion σ2 corresponds to the variance.
As the risk measure consists of the probability that the return falls below a given barrier λ, we can estimate the risk measure by the ratio between the number of observations being smaller than λ and the total number of observations in the sample.
Value at Risk
Value at risk (VaR1−α) is a closely related possible safety-first measure of risk defined by the following equality:
Here, 1 − α is denoted as the confidence level and α usually takes values like 1% or 5%. Theoretically, the VaR figure defined by equation (7) can admit negative values. In reality, however, it is likely and often implicitly assumed that the VaR is positive, and it can be interpreted as the level at which the losses will not exceed with a probability of 1 − α%. Sometimes VaR is, therefore, defined as the maximum of zero and the expression defined in equation (7) to guarantee a positive value for VaR.
VaR can be used as a risk measure to determine reward-risk optimal portfolios. Moreover, this simple risk measure can also be used by financial institutions to evaluate the market risk exposure of their trading portfolios. The main characteristic of VaR is that of synthesizing in a single value the possible losses that could occur with a given probability in a given temporal horizon. This feature, together with the (very intuitive) concept of maximum probable loss, allows the nonexpert investor to figure out how risky the position is and the correcting strategies to adopt. Based on a sample of return observations, VaR estimates coincide with the empirical alphaquantile. VaR and sophisticated methodologies for estimating VaR are explained in Chapter of Rachev, Menn, and Fabozzi (2005).
Conditional Value at Risk/Expected Tail Loss
The conditional value at risk (CVaR1−α) or expected tail loss (ETL) is defined as:
(8) ![]()
where VaR1−α(X) is defined in equation (7) and we assume that portfolio return distribution is continuous.10 From this definition we observe that the CVaR can be seen as the expected shortfall assuming the VaR1−α(X) as the benchmark.
A sophisticated estimation of CVaR depends strongly on the estimation of VaR. An explanation and illustration of the calculation of CVaR is provided in Rachev, Menn, and Fabozzi (2005). Based on a large sample of observations, a natural estimate for CVaR can be obtained by averaging all observations in the sample that are smaller than the corresponding VaR estimate.
MiniMax
An alternative way to derive some safety-first optimal portfolios is minimizing the MiniMax (MM) risk measure (see Young, 1998). The MiniMax of a portfolio return is given by:
(9) ![]()
This risk measure can be seen as an extreme case of CVaR.
Lower Partial Moment
A natural extension of semivariance is the lower partial moment risk measure (see Bawa, 1976, and Fishburn, 1977) also called downside risk or probability-weighted function of deviations below a specified target return. This risk measure depends on two parameters:
The lower partial moment of a portfolio rp bounded from below is given by
where q is the power index and t is the target rare of return.
Given a sample of return observations, we can approximate equation (10) as follows:

where as before
![]()
denotes the sample mean of the portfolio return.
Power Conditional Value at Risk
The power conditional value at risk measure, introduced in Rachev, Jasic, Biglova, and Fabozzi (2005), is the CVaR of the lower partial moment of the return. It depends on a power index that varies with respect to an investor's degree of risk aversion. Power CVaR generalizes the concept of CVaR and is defined as
(11) ![]()
A sample version of power CVaR can be obtained in the same way as sample version for the regular CVaR, that is, one calculates the q-th sample moment of all observations in the sample that are smaller than the corresponding VaR estimate.
KEY POINTS
- While the underpinning of financial theory is that the distribution of the return on financial assets is normally distributed, little evidence supports this assumption. Consequently, the justification for the use of the standard deviation or variance as a measure of risk in financial applications such as portfolio selection is difficult to justify.
- Alternative risk measures that can accommodate the properties of asset returns that have been observed in financial markets have been proposed.
- Alternative risk measures include dispersion measures and safety-first risk measures.
- Dispersion measures include mean standard deviation, mean absolute deviation, mean absolute moment, index of dissimilarity, mean entropy, and mean colog.
- Safety-first risk measures include classical safety first, value at risk, conditional value at risk, expected tail loss, MiniMax, lower partial moment, downside risk, probability-weighted function of deviations below a specified target return, and power conditional value at risk.
NOTES
1. See Ryan and Fabozzi (2002).
2. The mean semivariance approach was revisited by Stefani and Szegö (1976).
3. For more details, see Rachev, Menn, and Fabozzi (2006).
4. See Konno and Yamazaki (1991), Zenios and Kang (1993), Speranza (1993), and Ogryczak and Ruszczynski (2001).
5. For a further discussion of this index, see Rachev (1991).
6. See Buchen and Kelly (1996) and Avellaneda (1998).
7. See Giacometri and Ortobelli (2001).
8. See, among others, Roy (1952), Tesler (1955/6), and Bawa (1976, 1978).
9. See Castagnoli and LiCalzi (1996, 1999), Bordley and LiCalzi (2000), Ortobelli and Rachev (2001), Rachev and Mittnik (2000, pp. 424–464), and Rachev, Ortobelli, and Schwartz (2004).
10. See Bawa (1978), Uryasev (2000), and Martin, Rachev, and Siboulet (2003).
REFERENCES
Artzner, P., Delbaen, F., Eber, J-M, and Heath, D. (2000). Coherent measures of risk. Mathematical Finance 9: 203–228.
Artzner, P., Delbaen, F., Eber, J-M, Heath, D., and Ku, H. (2003). Coherent multiperiod measures of risk. Unpublished paper.
Avellaneda, M. (1998). Minimum entropy calibration of asset pricing models. International Journal of Theoretical and Applied Finance 1: 447–472.
Balzer, L. A. (2001). Investment Risk: A unified approach to upside and downside returns. In F. A. Sortino and S. E. Satchell (eds.), Managing Downside Risk in Financial Markets: Theory Practice and Implementation (pp. 103–155). Oxford: Butterworth-Heinemann.
Bawa, V. S. (1976). Admissible portfolio for all individuals. Journal of Finance 31: 1169–1183.
Bawa, V. S. (1978). Safety-first stochastic dominance and optimal portfolio choice. Journal of Financial and Quantitative Analysis 13: 255–271.
Bordley, R., and LiCalzi, M. (2000). Decision analysis using targets instead of utility functions. Decision in Economics and Finance 23: 53–74.
Buchen, P. W., and Kelly, M. (1996). The maximum entropy distribution of an asset inferred from option prices. Journal of Financial and Quantitative Analysis 31: 143–159.
Castagnoli, E., and LiCalzi, M. (1996). Expected utility without utility. Theory and Decision 41: 281–301.
Castagnoli, E., and LiCalzi, M. (1999). Non-expected utility theories and benchmarking under risk. SZIGMA 29: 199–211.
Dowd, K. (2002). Measuring Market Risk. Chichester: John Wiley & Sons.
Engle, R. F. (1982). Autoregressive conditional heteroskedasticity with estimates of the variance of U.K. inflation. Econometrica 50: 987–1008.
Engle, R. F., and Granger, C. W. J. (1987). Cointegration and error correction: Representation, estimation, and testing. Econometrica 55: 251–276.
Fishburn, P. C. (1977). Mean-risk analysis with risk associated with below-target returns. American Economic Review 67: 116–126.
Fritelli, M., and Rosazza Gianin, E. (2004). Dynamic convex risk measures. In G. Szegö (ed.), Risk Measures for the 21st Century (pp. 227–249). Chichester, UK: John Wiley & Sons.
Giacometti, R., and Ortobelli, S. (2004). Risk measures for asset allocation models. In G. Szegö (ed.), Risk Measures for the 21st Century (pp. 69–87). Chichester, UK: John Wiley & Sons.
Gini, C. (1921). Measurement of inequality of incomes. The Economic Journal 31: 124–126.
Gini, C. (1965). La dissomiglianza. Metron 24: 309–331.
Granger, C. W. J. (1981). Some properties of time series and their use in econometric model specification. Journal of Econometrics 16: 121–130.
Konno, H., and Yamazaki, H. (1991). Mean-absolute deviation portfolio optimization model and its application to Tokyo Stock Market. Management Science 37: 519–531.
Markowitz, H. M. (1952). Portfolio selection. Journal of Finance 7: 77–91.
Markowitz, H. M. (1959). Portfolio Selection: Efficient Diversification of Investment. New York: John Wiley & Sons.
Martin, D., Rachev, S. T., and Siboulet, F. (2003). Phi-Alpha optimal portfolios and extreme risk management. Willmot Magazine of Finance, November: 70–83.
Ogryczak, W., and Ruszczynski, A. (2001). On consistency of stochastic dominance and mean-semideviation models. Mathematical Programming 89: 217–232.
Olsen, R. A. (1997). Investment risk: The experts’ perspective. Financial Analysts Journal, March/April: 62–66.
Ortobelli, S. (2001). The classification of parametric choices under uncertainty: Analysis of the portfolio choice problem. Theory and Decision 51: 297–327.
Ortobelli, S., and Rachev, S. T. (2001). Safety first analysis and stable Paretian approach. Mathematical and Computer Modelling 34: 1037–1072.
Ortobelli, S., Huber, I., and Schwartz, E. (2002). Portfolio selection with stable distributed returns. Mathematical Methods of Operations Research 55: 265–300.
Ortobelli, S., Huber, I., Rachev, S. T., and Schwartz, E. (2003). Portfolio choice theory with non-Gaussian distributed returns. In S.T. Rachev (ed.), Handbook of Heavy Tailed Distributions in Finance (pp. 547–594). Amsterdam: North Holland Handbooks of Finance.
Philippatos, G. C., and Wilson, C. J. (1972). Entropy, market risk and the selection of efficient portfolio. Applied Economics 4: 209–220.
Philippatos, G. C., and Gressis, N. (1975). Conditions of equivalence among E-V, SSD and E-H portfolio selection criteria: The case for uniform, normal and lognormal distributions. Management Science 21: 617–625.
Rachev, S. T. (1991). Probability Metrics and the Stability of Stochastic Models. New York: John Wiley & Sons.
Rachev, S. T., and Gamrowski, S. (1995). Financial models using stable laws. In Y. V. Prohorov (ed.), Probability Theory and Its Application in Applied and Industrial Mathematics, Vol. 2 (pp. 556–604), New York: Springer Verlag.
Rachev, S. T., Jasic, T., Biglova, A., and Fabozzi, F. J. (2005). Risk and return in momentum strategies: Profitability from portfolios based on risk-adjusted stock ranking criteria. Technical report, Chair of Econometrics, Statistics and Mathematical Finance, School of Economics, University of Karlsruhe, Postfach 6980, D-76128, Karlsruhe, Germany and Technical Report, Department of Statistics and Applied Probability, UCSB, CA 93106, USA.
Rachev, S. T., Menn, C., and Fabozzi, F. J. (2005). Fat-Tailed and Skewed Asset Return Distributions: Implications for Risk Management, Portfolio Selection, and Option Pricing. Hoboken, NJ: John Wiley & Sons.
Rachev, S. T., and Mittnik, S. (2000). Stable Paretian Model in Finance. Chichester: John Wiley & Sons.
Rachev, S., Ortobelli, S., and Schwartz, S. (2004). The problem of optimal asset allocation with stable distributed returns. In A. Krinik and R. J. Swift (eds.), Stochastic Processes and Functional Analysis: A Dekker Series of Lecture Notes in Pure and Applied Mathematics (pp. 295–361), New York: Dekker.
Roy, A. D. (1952). Safety-first and the holding of assets. Econometrica 20: 431–449.
Ryan, R., and Fabozzi, F. J. (2002). Rethinking pension liabilities and asset allocation. Journal of Portfolio Management 28, 4: 7–15.
Shalit, H., and Yitzhaki, S. (1984). Mean-Gini, portfolio theory, and the pricing of risky assets. Journal of Finance 39: 1449–1468.
Sortino, F. A., and. Satchell, S. E. (eds.) (2001). Managing Downside Risk in Financial Markets: Theory Practice and Implementation. Oxford: Butterworth-Heinemann.
Speranza, M. G. (1993). Linear programming models for portfolio optimization. Finance 14: 107–123.
Stefani, S., and Szegö, G. (1976). Formulazione analitica della funzione utilità dipendente da media e semivarianza mediante il principio dell’utilità attesa. Bollettino UMI, 13A: 157–162.
Stoyanov, S. V., Rachev, S. T., and Fabozzi, F. J. (2008). Optimal financial portfolios. Forthcoming in Applied Mathematical Finance.
Szegö, G. (2004). On the (non)acceptance of innovations. In G. Szegö (ed.), Risk Measures for the 21st Century (pp. 1–10). Chichester, UK: John Wiley & Sons.
Tesler, L. G. (1955/6). Safety first and hedging. Review of Economic Studies 23: 1–16.
Tobin, J. (1958). Liquidity preference as behavior toward risk. Review of Economic Studies 25: 65–86.
Uryasev, S. P. (2000). Probabilistic Constrained Optimization Methodology and Applications. Dordrecht: Kluwer Academic Publishers.
Von Neumann, J., and Morgenstern, O. (1953). Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press.
Young, M. R. (1998). A MiniMax portfolio selection rule with linear programming solution. Management Science 44: 673–683.
Zenios, S. A., and Kang, P. (1993). Mean absolute deviation portfolio optimization for mortgage-backed securities. Annals of Operations Research 45: 433–450.
