2.6 Statistical Signal Processing

It is known that a cell's response in the brain is a spiking train with almost out-of-order timing (random), so its response strength has to be estimated by its mean firing rate within a fixed interval. Human vision receives a large number of signals from the environment, and this results in a great deal of cells firing in various areas of the brain at all times. How can we depict the activity of the cell population across time and space? From the view of signal processing and computer vision, the concepts of probability distribution, other statistical properties and signal detection and estimation with statistical signal processing theory need to be considered in visual attention modelling.

Many computational visual attention models are based on information theory and statistical signal processing, and detailed discussions will be given in the next chapter. This section simply introduces the relationship between visual attention and these relevant theories, which mainly consist of the following three aspects.

The following three subsections will give detailed descriptions of visual attention based on these three relevant theories.

2.6.1 A Signal Detection Approach for Visual Attention

Signal detection theory (SDT) is used to analyse ambiguous data coming from experiments. Ambiguous data are obtained by a known process (signal) or by chance (noise), and in general the signal is embedded in noise. Consider the signal and noise measurements from the experiments as two different random variables that satisfy certain probability density distributions. The motivation of detection theory is to estimate a detection threshold that can separate signal and noise when the probability density distributions of the two random variables are given. Without loss of generality, suppose that a random variable, x, is depicted as the bell-shaped Gaussian distribution function as

(2.5)

where μ and σ respectively denote the mean value and deviation of x. Random variables representing signal and noise have different mean values and deviations: for signal, μ₁ = a, a > 0,σ = σ₁ and for noise, μ₂ = 0, σ = σ₂. A ‘yes' response given to a stimulus as a correct response is called a hit, but a ‘yes' response to a stimulus as a mistake is called a false alarm. The strategy of signal detection is to find the threshold, th, 0 < th < a, which maximizes the hits and minimizes the false alarms, for given density distributions. The effect of signal detection depends on the distance between the signal and the noise density distribution. Let σ = σ₁ = σ₂ for simplicity. It is obvious that if a 0 and σ is small, the two Gaussian curves for signal and noise separate well, and it is easy to find a threshold th such that the signal can be detected from the noise. Contrarily, if a ≈ 0 or σ is large, the two Gaussian curves overlap, and this results in more false alarms and fewer hits. Thereby, the discrimination of the signal and noise is dependent of a/σ. An illustration of this will be given in Figure 2.18(a) and (b).

Some researchers have suggested that the standard SDT model can be applied to visual search, because the task of finding the target among distractors or clutter (background) has the same aim as SDT [121]. Let us consider the case of Figure 2.8(a), an easy search, and the cases of Figure 2.8(b) and (c), which have search difficulty. SDT can interpret these cases very easily, when the target is regarded as the signal and the distractors as noise. Each element in visual search display is represented as an independent, random variable when it is monitored by an observer for testing several times with some testing error. Assume that there exists a matching filter (detector) with a preferred orientation and RF size. Then, if each element in the display is scanned by the filter, and the mean and deviation of their responses are computed, obviously the target is associated with higher mean value than the distractors due to the better matching between the filter and the target. For simplicity, both probability densities of responses for the target (signal) and distractors (noise) are assumed to be Gaussian functions as Equation 2.5 with the same standard deviation σ and different mean values, μ₁ and μ₂, respectively. Since the detector is designed to match with the target, the response of the target must be greater than those of distractors, i.e., μ₁ > μ₂ > 0. Note that this is different from the classical SDT model, because the response to a distractor is not zero mean, that is μ₂ ≠ 0. The discriminating index of the target from the distractors, D_r, is defined as

(2.6)

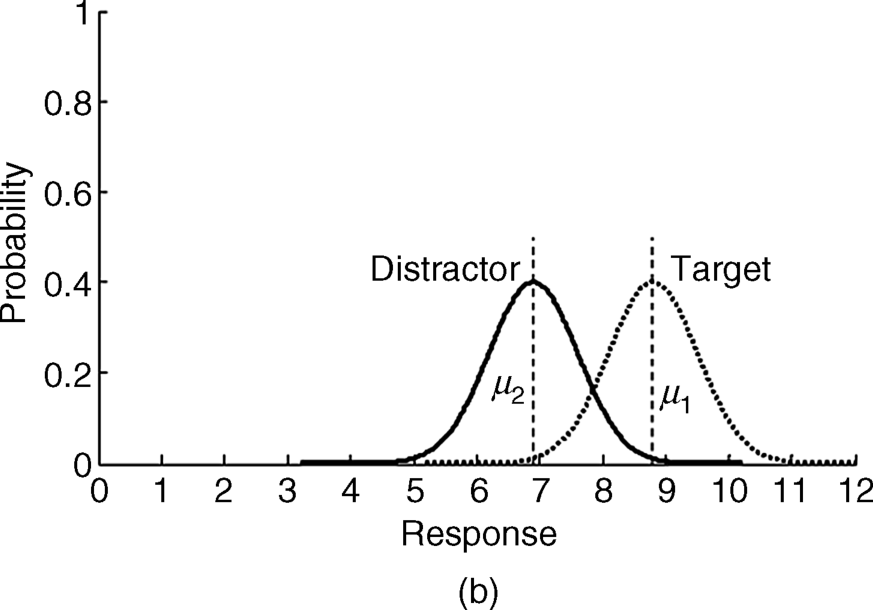
For the case of Figure 2.8(a), since the matching filter prefers (to match) the target (the slanted-vertical bar), the observed values have much higher mean value than that for the distractors (45° bars), so the Gaussian curves of both target and distractors are separated as in Figure 2.18(a), and the discriminating index D_r, is high.

Observers can detect the target quickly by using threshold th = 6.5 for the case of Figure 2.18(a). For the case of Figure 2.8(b), the similarity between the target and distractors increases, so the mean value of target, μ₁, approaches to the mean value of the distractors μ₂, with the resultant overlapping of both Gaussian curves that are exemplified in Figure 2.18(b). The detection difficulty of Figure 2.8(b) is explained clearly because the discriminating index D_r, decreases. In the case of the distractors' heterogeneity in Figure 2.8(c), the deviation of the distractors' measurements makes σ₂ greater and this leads to detection difficulty on account of the overlapping of the two Gaussian distribution curves for a similar reason to Figure 2.8(b).

2.6.2 Estimation Theory and Visual Attention

Estimation theory is a branch of statistical signal processing that estimates the values of parameters based on measured or empirical data with random components. Suppose that the probability density distribution of an observable random variable x for an experiment depends on a parameter θ (or a parameter vector θ if there are many parameters, which require estimation, as in a multidimensional feature case). Here we only consider the parameter in one dimension for simplicity. There are T scalar measurements x: x(1), x(2) . . . x(T). The parameter θ can be estimated from these measurements:

(2.7)

where E is the expected value operator, and 2.7 finds the conditional expected value of parameter θ. There are many parameter estimation methods in estimation theory, such as least squares estimation, maximum likelihood method and so on. An influential estimation method developed in 1930s is Bayesian estimation in which there are two probability density functions: prior and posterior densities.

First, prior probability is the probability density of the parameter, θ, which is assumed to be a random variable itself. Its probability density is known in advance, which is to reflect knowledge of the parameter before measuring the data. In Bayesian theory, the estimation of a parameter not only needs information about the measurements, but also needs a prior probability density of the estimated parameter, which is an essential element in the estimation process.

Second, posterior probability is the conditional probability of parameter θ, given the measurements x(1), x(2) . . . x(T) and prior probability density of θ. It is an updated probability, given information on the measured data. Let us denote the prior probability density of parameter, θ, as p(θ) and the conditional probability of the observations as p(X/θ), given parameter θ, where X = {x(1), x(2) . . . x(T)}. The posterior probability estimation of θ can be computed from the Bayesian equation as

(2.8)

with

Equation 2.8 represents the transform from prior probability to posterior probability. Based on the posterior probability, the conditional expected value E (θ/X) is a Bayesian estimation of parameter θ.

What attracts human attention? A motorboat that suddenly appears on a calm sea or an unidentified flying object that appears in a blue sky often attracts human attention, because these objects are unexpected targets across spatiotemporal scales. Itti et al. proposed a surprise concept to measure attention based on the Bayesian framework [122]. If the prior probability is from an observer's knowledge and experience in the background, it will be defined as {p(M)_MM} over the model M in a model space M. The new data X, just recently received by the observer, changes the prior probability {p(M)_MM}to the posterior probability {p(M/X)}_MM via the Bayesian Equation 2.8. We have

(2.9)

The difference between Equations 2.8 and 2.9 is that the parameter θ is replaced by prior knowledge M. Since surprising or unexpected objects in a scene often attract human attention, the difference between prior and posterior probability density can be adopted to measure the surprise. It is known that the Kullback–Leibler (KL) divergence is often used to test the difference between probability density [123]. The surprise is defined by the average of the log-odd ratio:

(2.10)

Obviously, visual attention is proportional to KL divergence. The related issues on surprise-based computational attention models will be discussed in more detail in Chapter 3.

2.6.3 Information Theory for Visual Attention

Information theory is a branch of applied mathematics and electrical engineering, which is related to the quantification of information. A key measure of information is known as entropy. Entropy quantifies the uncertainty involved in predicting the value of a random variable. For arbitrary random variable x, its entropy H of x is defined as

(2.11)

where E again denotes the expectation, and I_s(x) is the self-information for x in a concrete range. I_s(x) also is a random variable. Let p represent the probability density function. For a discrete random variable, x, as a set of all discrete messages {a₁, a₂, . . . , a_n}, the entropy contribution of an individual message is the negative logarithm of the probability density for the individual message. Equation 2.11 can be written as

(2.12)

It is noticed that the entropy, H(x), has the following properties: (1) H(x) is always greater than or equal to zero. (2) If the probabilities p(X = a_i) are close to 0 or 1, the entropy is small. Consider that a_i is the ith greyscale in a digital image with n greyscales. p(x = a_i) = 1 and p(x ≠ a_i) = 0 mean that the identical greyscale appears on all pixels of the image. There is no information on the image, so H(x) = 0. The image with no information will not attract any attention. (3) If all the probabilities are more than 0 and less than 1, the entropy will be large. The HVS pays attention to the place or scene with high entropy, and thus self-information or entropy is often used to measure the attention location in computational visual attention models.

Another very interesting fact related to the HVS is that RFs of simple cells in the brain have been developed via capturing useful information from the outside environment. Based on the biological findings, some cells in the V1 area adapt their weights, from input RFs to the cells, in the critical period of vision development. Hence, each of these cells has different preferred orientations in the same RF due to the exposure to natural scenes with abundant orientation edges. This kind of adaptation was confirmed in an early experiment [124], in which some newborn kittens were raised in an environment displaying only vertical gratings. Six weeks after their birth, the orientation sensitivity for the population of cells in the primary visual cortex was found to largely concentrate around the vertical orientation. This means that the profiles of RFs are developed by the information obtained from the outside environment. Moreover, only useful information is utilized for learning the connections of cells, and also redundant or repeating information in a scene is discarded. For example, the RF of preferred-orientation cells only extracts the edges in natural scenes. In general, the natural environment is structured to represent a certain sense (or meaning) to us. Some correlation between context and information redundancy exists in natural scenes; for instance, the scene of a ship on a blue ocean or birds in a forest, in which there is much correlation or redundancy (repeating blue pixels in the ocean area or the some structured branches in the forest) that has to be discarded in the developmental process in our HVS. Obviously, the goal of early visual development is the same as the aim of visual attention in the sense of reducing redundancy and popping out the interesting targets (the ship or birds). Since the visual development process is based on statistical signal processing, some concepts of information theory can be applied to understanding and modelling visual attention.

There are two information processing strategies to be described for reducing redundancy in early visual coding. One is based on decorrelation or compact coding, called principal components analysis (PCA), and the other is sparse distributed coding or referred to as independent components analysis (ICA) which more effectively represents the input information or makes its entropy approach the maximum after coding. Both PCA and ICA correspond to RFs' developmental process in the HVS, that is the complex interaction of the cells with the environment.

Suppose that the input image sequence is represented as a random vector input stream: x(1), x(2), . . . , x(T), x(t) R^l, l = m × n, where m and n are the length and width of input image or a patch of image. The dimension l (or T) can be very large. We then denote the data by x_i (t) i = 1,2,3 . . . l where x_i (t) is a random variable at the ith component in random vector x. The output of coding is y(t) R^k, in general, k ≤ l. The coding procedure aims to reduce redundancy in the input stream. If there is a linear relation between the input image stream and the output of the coding, the two strategies (PCA and ICA) can be implemented by feed-forward neural networks as shown in Figure 2.19. The connections between neurons and input vector x(t) are defined by matrix W, and the connection vector of one neuron (one output neuron) is its connection vector denoted as w_j, and j = 1,2, . . . k for k output neurons. This linear transform, Equation 2.13, from x(t) to y(t) by weight matrix W can be used to describe the neural network structure in Figure 2.19.

(2.13)

Figure 2.19 Neural networks for PCA and ICA, with the circles denoting neurons

In Equation 2.13, n is noise (or error) vector while using y to describe x, where n R^k, and n_j is the component of vector n. We omit the time variable t for simplicity. Assume x to be a random vector with highly correlated context. Given x, we hope to determine the matrix W by the statistical properties of the transformed y such that it is more efficient to represent x, that is y has less redundancy.

PCA is an important technique for reducing correlation which uses second-order statistics to reduce signals' correlation or redundancy. If x(t), t = 1,2, . . . , is given, the first-order statistic m_x and second-order statistic C_xx of x can be estimated as

(2.14)

where E(x) represents the expectation of the input stream x for all the time t. Mathematically, the solution of PCA is given in terms of the eigenvectors e₁, e₂, . . . e_l of the covariance matrix C_xx. The ordering of the eigenvectors follows the order of corresponding eigenvalues; that is, the eigenvectors e₁ is for the largest eigenvalue, e₂ is for the second largest eigenvalue and so on. The first principal component of x is , and the lth principal component of x is . Since the inner products of the input vector and eigenvectors corresponding to small eigenvalues are insignificant, they can be omitted. If w_i = e_i, i = 1, 2, . . . k, k < l, then the matrix W in Equation 2.14 consists of the eigenvectors corresponding to the k largest eigenvalues and the principal components are the output of neurons, y_j, j = 1, 2, . . . k.

PCA reduces the dimension of vectors (k < l) with minimal root mean square error between the input and the new representation (output). In addition, the output of each neuron in the neural network, y_i, is uncorrelated with all the other outputs after PCA, though the input image is highly correlated. We have

(2.15)

Hereby, PCA can decorrelate between pixels of the input image sequence and reduce the redundancy in images. In fact, these connections between neurons and their inputs in the feed-forward neural network of Figure 2.19 can be obtained by a learning rule (e.g., the Hebbian rule, discovered in cell activity in 1949 [125]). A simulation of RF development can be found when these neurons (the top row in Figure 2.19) represent simple cells in the primary visual cortex, and input x represents the sequence of input stimuli in the RF on the retina. Considering the lateral inhibition effect, the optimal compact code learning via the Hebbian rule for displaying a patch of natural stream scene can provide the profiles of weight vectors for these neurons much like those cells found in the early visual cortex. For instance, the connections for different preferred orientation cells are found in the same RF [126, 127], and the connection profiles of colour opponent cells are found while inputting chromatic random grating images [128]. Evidently, our visual system always reduces redundancy from a mass of input images at all the time since the time we were born. The connection profiles of all the simple cells as feature extraction channels mentioned in Section 2.1 are the results of reducing redundancy by learning.

However, as concluded by the several studies, PCA is insufficient to account for the receptive field properties since it can only produce some RF profiles in global information, but not for localized RFs [127]. More reasonable analysis can be done based on high-order statistics to reduce redundancy by ICA. If input random vector (observed vector) x can be regarded as the product of a source vector composed of some unknown independent random components, s, and an unknown mixing matrix A, ICA can approximately estimate both source vector s and mixing matrix A by using the property of high-order statistical independence between the neurons' outputs in Figure 2.19. The basic equation of observed vector is:

(2.16)

where

(2.17)

and p(s) is the joint probability density of all the random independent components s₁, s₂, . . . , s_k, and p(s_i) is the probability density of random component s_i. When the observed vector x is input to the feed-forward neural network in Figure 2.19, the connections W can be adapted by some statistical independent criteria, such that the following equation is satisfied:

(2.18)

Obviously, the components of output vector y are statistically independent of each other, and their shapes are similar to the components of source vector s, but there may be order permutation and amplitude changes.

It should be noted that, in a general algorithm, the noise item in Equation 2.16 is often omitted and the dimension l of observed vector x is reduced to the same as the dimension of the source vector k as previously used by PCA, so the matrix W is often a k × k square matrix. The learning rules for ICA are: maximum entropy, minimizing mutual information and maximum non-Gaussian. The maximum entropy criterion makes the entropy of the neural network's output signal, H(y), maximum via adapting weight matrix W, to capture maximum quantification of information from a mass of visual inputs. Minimizing mutual information is to reduce the high-order correlation between the output's components, and maximizing non-Gaussian is based on the Gaussian distribution property of mixing signals that are different from independent sources. There are a lot of learning rules and detailed steps of algorithms about ICA. We will not give the details here; the interested reader can find the relevant work in literature [129–131].

An interesting issue about ICA is that an optimal representation for natural scenes is based on ICA learning results, because the weight vectors after ICA learning appear much more like RF profiles, including some localized RFs that PCA does not have. These results were first found in 1996 by Olshausen and Field [132]: when the input x of a neural network is some small patches of natural scenes corresponding to the cell's RF on the retina, after ICA, the weight vectors on different neurons appear in different preferred orientation profiles at different places and sizes. Afterwards, almost the same results were obtained in [129–131] by using different criteria. Otherwise, the output of a neural network represents a sparsely distributed coding for input scenes. In a sparse distributed code, the dimensionality of the representation is maintained, but the number of cells responding to any particular input is minimized [127].

Since the goal of development of PCA and ICA is to maximize information extraction from the input scene, which has the same purpose as visual attention, and since the information entropy is a measure of quantity of information, both PCA and ICA are often used in visual attention computational models.