
Chapter Eleven — Polynomials
The Humongous Book of Algebra Problems
251
Therefore, .
11.36 Calculate (5x
3
+ 6x
2
– 3) ÷ (x
2
– 1) using long division.
Both the dividend and the divisor are missing powers of x. Neither contains an
x
1
-term, so insert the placeholder 0x into each one before dividing.
Therefore, .
Synthetic Division of Polynomials
Divide using only the coefcients
11.37 Explain why synthetic division cannot be used to calculate (x
3
+ 1) ÷ (x
2
+ 1).
Synthetic division, a technique used to divide polynomials that is simpler and
more compact than long division, can only be applied when the divisor is a
linear binomial. In this problem, the divisor x
2
+ 1 is a quadratic binomial, so
long division must be used to calculate the quotient.
11.38 Calculate (x
2
– 4x – 12) ÷ (x – 6) using synthetic division.
List the coefficients of the dividend in a horizontal row. Note that x
2
does not
have an explicitly stated coefficient, so the implied coefficient is 1. Beneath the
coefficients, draw a horizontal line.
To the left of the numbers, list the opposite of the constant in the divisor.
Separate it from the coefficients using a box, as demonstrated below.
Drop the leftmost coefficient, 1, below the horizontal line.
It’s a quadratic
because the highest
power of x is 2. It’s a
binomial because there
are two separate
terms.
The constant
in the divisor
x – 6 is –6. Take
the opposite of that
number and put it
here.

Chapter Eleven — Polynomials
The Humongous Book of Algebra Problems
252
Multiply the boxed number (6) by the number below the horizontal line (1) and
write the result (1 · 6 = 6) between the next coefficient (–4) and the horizontal
line.
Add –4 and 6 (–4 + 6 = 2) and write the sum in the same column as those
values, below the horizontal line.
Multiply the boxed number (6) by the newly placed value beneath the
horizontal line (2) and write the result (6 · 2 = 12) between the final coefficient
(–12) and the horizontal line.
Combine the numbers in the rightmost column (–12 + 12 = 0) and write the
result in the same column, below the horizontal line.
The numbers below the horizontal line represent the coefficients of the
quotient and the remainder. Note that the degree of the quotient is always one
less than the degree of the dividend, so this quotient has degree one: 1x + 2, or x
+ 2. The rightmost number below the horizontal line represents the remainder,
which is 0 for this problem.
Therefore, (x
2
– 4x – 12) ÷ (x – 6) = x + 2.
11.39 Calculate (3x
2
+ 5x – 1) ÷ (x + 4) using synthetic division.
Place the coefficients of the dividend in a horizontal row and the opposite of the
divisor’s constant to the left of those values, separated by a box. Beneath the row
of numbers, draw a horizontal line.
Drop the first coefficient (3) below the horizontal line, multiply it by the boxed
number (–4), and write the result (–4 · 3 = –12) between the next coefficient
(5) and the horizontal line.
The dividend
is x
2
– 4x – 12,
which has degree two
(because the highest
power of x is two). The
degree of the quotient
is one less, so its rst
term has degree
one: x
1
.
The divisor
is x + 4, so write
–4 (the opposite of
the constant) in a
box left of the
coefcients.

Chapter Eleven — Polynomials
The Humongous Book of Algebra Problems
253
Add the values in the second column of coefficients (5 – 12 = –7), and write the
result in the same column below the horizontal line.
Multiply the newly placed value (–7) by the boxed number (–4), write the
product (–4 · –7 = 28) between the final coefficient value (–1) and the
horizontal line, and add the numbers in that column (–1 + 28 = 27).
The degree of the quotient is one (exactly one less than the degree of the
dividend, which is two), so the numbers below the horizontal line, from left
to right, represent the coefficient of x
1
(3), a constant (–7), and the remainder
(27).
11.40 Calculate (2x
3
– 9x
2
– 51x – 40) ÷ (x – 8) using synthetic division.
Apply the synthetic division technique described in Problems 11.38–11.39.
The degree of the quotient is two, which is one less than the degree of the
dividend. Therefore, the numbers below the horizontal line represent, from left
to right, the coefficient of x
2
, the coefficient of x, a constant, and the remainder.
Therefore, (2x
3
– 9x
2
– 51x – 40) ÷ (x – 8) = 2x
2
+ 7x + 5.
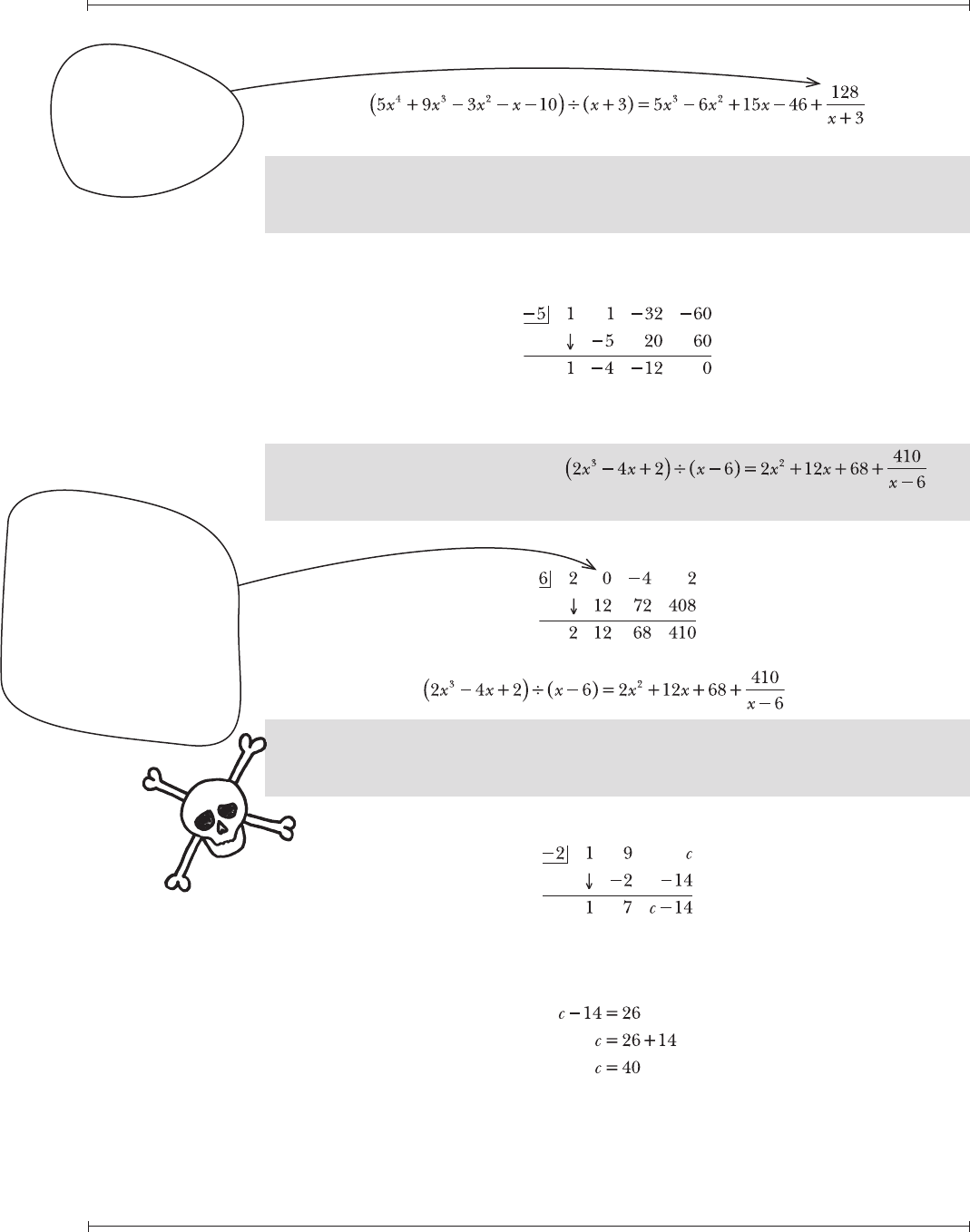
11.41 Calculate (5x
4
+ 9x
3
– 3x
2
– x – 10) ÷ (x + 3) using synthetic division.
Rewrite the expression as a synthetic division problem to calculate the values of
the quotient and remainder.
RULE
OF THUMB:
Multiply the
numbers below
the horizontal line
by the number in
the box and write
the result above the
horizontal line in the
next column. Add
the numbers in that
column, write the
answer below the
horizontal line,
and repeat.
Chapter Eleven — Polynomials
The Humongous Book of Algebra Problems
254
The degree of the quotient is 3, one less than the degree of the dividend.
11.42 According to Problem 11.34, (x
3
+ x
2
– 32x – 60) ÷ (x + 5) = x
2
– 4x – 12. Verify
the quotient using synthetic division.
Rewrite the expression as a synthetic division problem to calculate the values of
the quotient and remainder.
Therefore, (x
3
+ x
2
– 32x – 60) ÷ (x + 5) = x
2
– 4x – 12.
11.43 According to Problem 11.35, .
Verify the solution using synthetic division.
Rewrite the expression as a synthetic division problem.
Therefore, .
11.44 Calculate the value of c in the expression (x
2
– 9x + c) ÷ (x + 2) if the remainder
is 26.
Use synthetic division to calculate (x
2
– 9x + c) ÷ (x + 2).
Set the remainder calculated above (c – 14) equal to the stated remainder (26)
and solve for c.
Divide the
remainder 128
by the divisor,
x + 3.
The dividend is
missing an x
2
-term,
so just like you have
to include 0x
2
to long
divide in Problem 11.35,
you have to include
the 0 coefcient to
divide synthetically.

Chapter Eleven — Polynomials
The Humongous Book of Algebra Problems
255
11.45 Calculate the value of a in the expression x
3
+ ax
2
– 61x + 14 if x + 7 divides
evenly into the cubic polynomial.
Apply synthetic division to calculate (x
3
+ ax
2
– 61x + 14) ÷ (x + 7).
If x + 7 divides evenly into x
3
+ ax
2
– 61x + 14, then the remainder (49a + 98) is
equal to 0. Express this using an equation and solve it for a.
When you
multiply a – 7 by –7
(the number in
the box), you get
–7(a – 7) = –7a – 7(–7) =
–7a + 49. Add that to
–61 by combining the
constants: –61 + (–7a
+ 49) = –7a + (–61 +
49) = –7a – 12.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
