2.2 ALGEBRA

2.2.1 Groups

Definition 2.10 A group (G, *, 1) consists of a set G with a binary operation * and an identity element 1 satisfying the following three axioms:

1. 
2. 
3. for each element x of G there exists an element x⁻¹, called the inverse of x, such that

   

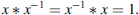
   If, furthermore,

4. (commutativity), the group is said to be commutative (or Abelian).
   Axioms 1 and 2 define a semigroup.

Examples 2.6

(Z, +, 0), (Z_n, +, 0), (, ., 1)

The following definitions generalize Definitions 2.9.

Definitions 2.11

1. The order of an element x of a finite group G is the least positive integer t such that

   

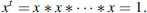
2. If the order of x is equal to the number n of elements in G, then x is said to be a generator of G.
3. If G has a generator, then G is said to be cyclic.

Property 2.6 The order of an element x of a finite group G divides the number of elements in G..

Proof First observe that if H is a subgroup of G, then an equivalence relation on G can be defined: g₁ ≡ g₂ if there exists an element h in H such that g₁.h = g₂. The number of elements in an equivalence class is equal to the number |H| of elements in H. Thus the number |G| of elements in G is equal to |H|.|G/H|, with G/H the set of classes and |G/H| the number of classes. In other words the number of elements of a subgroup divides the number of elements of the group. It remains to observe that the set {x, x², …, x^t = 1}, where t is the order of x, is a subgroup, so that the number t of elements of the subgroup divides the number of elements in G.

Example 2.7

(, ., 1);

3 and 5 are generators;

the subgroup generated by 2 is {2, 4, 1}; the corresponding classes are then {2, 4, 1} and {6, 5, 3}; the number of elements (3) of the subgroup divides the number of elements (6) of .

2.2.2 Rings

Definition 2.12 A ring (R, +, *, 0, 1) consists of a set R with two binary operations + and *, an additive identity element 0, and a multiplicative identity element 1 satisfying the following axioms:

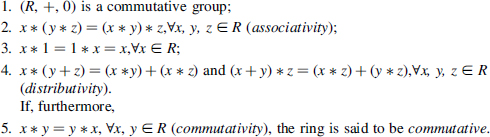
Examples 2.8

(Z, +, ., 0, 1), (Z_n, +, ., 0, 1)

2.2.3 Fields

Definition 2.13 A field (F, +, *, 0, 1) consists of a set F with two binary operations + and *, an additive identity element 0, and a multiplicative identity element 1 satisfying the following axioms:

1. (F, +, *, 0, 1) is a commutative ring;
2. all nonzero elements of F have a multiplicative inverse.

Example 2.9

(Z_p, +, ., 0, 1), where p is a prime.

2.2.4 Polynomial Rings

Definitions 2.14

1. If F is a field, then a polynomial in the indeterminate x over F is an expression of the form

   

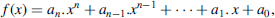
   where

2. The largest integer m (if any) such that a_m ≠ 0 is the degree of f(x). It is denoted deg(f) and a_m is called the leading coefficient. If all the coefficients of f(x) are equal to 0, then f(x) is called the zero polynomial and its degree defined to be equal to − ∞. The 0-degree polynomials are also called constant polynomials.
3. A monic polynomial is a polynomial whose leading coefficient is equal to 1.
4. The polynomial ring F[x] is the ring formed by the set of all polynomials in the indeterminate x with coefficients in F. The two operations are the standard polynomial addition and multiplication, with coefficient arithmetic performed in F. The additive identity element 0 is the zero polynomial. The multiplicative identity element 1 is the monic constant polynomial.

Definition 2.15 Thanks to the fact that F is a field, so that all the nonzero coefficients have an inverse, the standard polynomial division can also be performed. Thus, if g(x) and h(x) ≠ 0 are polynomials in F[x], then there exist two polynomials q(x) (the quotient) and r(x) (the remainder) in F[x] such that

Notation:

Definitions 2.16

1. Given two polynomials g(x) and h(x), h(x) divides g(x) (or h(x) is a divisor of g(x)) if there exists a polynomial q(x) such that g(x) = q(x).h(x).
2. Given two polynomials g(x) and h(x), not both equal to 0, the greatest common divisor of g(x) and h(x) is the monic polynomial of greatest degree which divides both g(x) and h(x).
3. gcd(0, 0) = 0.
4. A polynomial f(x) of degree at least 1 is said to be irreducible if it cannot be written as the product of two polynomials, each of positive degree.

A variant of the Euclidean algorithm for polynomials (VZG2003) expresses the greatest common divider of two polynomials g(x) and h(x) in the form

The algorithm is based on the fact that if u(x) and v(x) are two polynomials such that

that is,

then

where deg(r^!) < m, so that

where

so that

Furthermore,

The sequence of operations is almost the same as for computing the greatest common divider of two integers. A series of polynomials r(0), r(1), r(2), … are generated. Initially, assume that deg(g) > deg(h) and define

At each step the decomposition (2.8) is used:

so that

where

At the end of the step, r(i) and r(i + 1) are interchanged if deg(r(i)) < deg(r(i + 1)).

Operations:

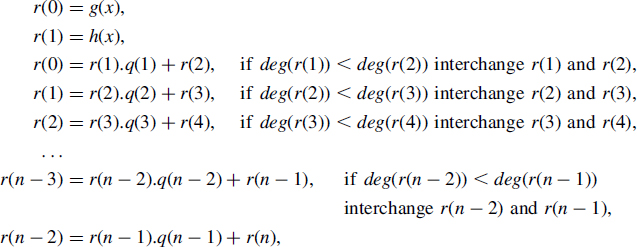
where

and

so that

Let r₀ be the coefficient of x⁰ in r(n). If r₀ = 0, then

If r₀ ≠ 0, then

In parallel with the computation of r(0), r(1), r(2), … , r(n), two series of polynomials b(i) and c(i) are generated:

It can be demonstrated by induction that

So, if r₀ = 0, then

and if r₀ ≠ 0, then

In the following algorithm u stands for r(i − 1), v for r(i), r for r(i + 1), b for b(i − 1), d for b(i), bb for b(i + 1), c for c(i − 1), e for c(i), and cc for c(i + 1):

Algorithm 2.3 Variant of the Extended Euclidean Algorithm for Polynomials

2.2.5 Congruences of Polynomial

Definition 2.17 Given three polynomials g(x), h(x), and f(x) in F[x], g(x) is congruent to h(x) modulo f(x) if f(x) divides g(x) − h(x).

Notation:

Properties 2.7 (Properties of Congruences)

1. g(x) ≡ h(x) (mod f(x)) if and only if (g(x) mod f(x)) = (h(x) mod f(x)) (Definition 2.15);
2. the relation g(x) ≡ h(x) (mod f(x)) is an equivalence relation (reflexive, symmetric, and transitive);
3. if g₁(x) ≡ h₁(x) (mod f(x)) and g₂(x) ≡ h₂(x) (mod f(x)), then

   

From Properties 2.7(1 and 2) it can be seen that the congruence relation partitions F[x] into equivalence classes. If n is the degree of f(x), then each equivalence class contains exactly one polynomial of degree d < n. So, if F is a finite field, then the number of equivalence classes is equal to |F|ⁿ, where |F| is the number of elements in F. Furthermore, according to Property 2.7(3), the addition, subtraction, and multiplication of congruence classes can be defined. As a matter of fact, the set of equivalence classes is isomorphic to

where the addition, the subtraction, and the multiplication are defined by

The set of equivalence classes is denoted F[x]/f(x).

Properties 2.8

1. F[x]/f(x) is a commutative ring.
2. If f(x) is irreducible, then F[x]/f(x) is a field.

Proof

1. Consequence of Property 2.7(3).
2. If f(x) is irreducible, then the greatest common divisor of f(x) and g(x) ≠ 0 is 1. Using the Euclidean algorithm (Algorithm 2.2), b(x) and c(x) can be computed such that

   

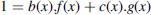
   and

   

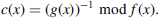
Definition 2.18 Let p be a prime, F = Z_p, and f(x) be an irreducible polynomial of degree n over Z_p. The corresponding field F[x]/f(x) contains q = pⁿ elements and is called either F_q or GF(q) (Galois field).

As a matter of fact, it can be demonstrated that any finite field contains q = pⁿ elements, for some prime p and some positive integer n, and is isomorphic to F_q (whatever the irreducible polynomial f(x) of degree n over Z_p). In particular, if n = 1, then the corresponding field F_p is isomorphic to Z_p.

The set of 0-degree polynomials (the constants) is a subfield of F_q isomorphic to F_p. If g(x) is a 0-degree polynomial (an element of F_p) then, according to the Fermat's little theorem, (g(x))^p = g(x). Conversely, it can be demonstrated that if a polynomial g(x) satisfies the condition (g(x))^p = g(x), then g(x) is a constant.

Another interesting property of F_q is that the set of nonzero polynomials is a cyclic group. Let g(x) be a nonzero polynomial, that is, an element of , and assume that the order of g(x) is t. According to the Property 2.6, t divides q − 1, so that (g(x))^q−1 = (g(x))^t.k = 1^k = 1. Consider now a polynomial g(x) and define h(x) = (g(x))^r, where r = (q − 1)/(p − 1). According to the previous property, (h(x))^p−1 = (g(x))^q−1 = 1 and (h(x))^p = h(x), so that h(x) is a constant polynomial.

A last property, useful for performing arithmetic operations, is that (g(x) + h(x))^p = (g(x))^p + (h(x))^p. It is a straightforward consequence of the fact that all the binomial coefficients (p!/(i!).(p − i)!) are multiples of p, except for i = 0 or p.

To summarize:

Properties 2.9 (Some Useful Properties of Finite Fields)

1. The set of 0-degree polynomials in F_q is a subfield of F_q isomorphic to F_p.
2. Given g(x) in F_p, then (g(x))^p = g(x) (Fermat's little theorem).
3. Given g(x) in F_q such that (g(x))^p = g(x); then g(x) ∈ F_p.
4. The set of nonzero polynomials of F_q is a cyclic group denoted .
5. Given g(x) in F_q, then (g(x))^q = g(x).
6. Given g(x) and h(x) in F_q, then (g(x) + h(x))^p = (g(x))^p + (h(x))^p.
7. If r = (pⁿ − 1)/(p − 1), that is, r = 1 + p + p² + … + pⁿ⁻¹, and g(x) is an element of F_q, then (g(x))^r is an element of F_p.

Example 2.10 p = 2, n = 4, f(x) = 1 + x + x⁴ so that x⁴ ≡ 1 + x mod f(x); α = x is a generator of the cyclic group :

Given a polynomial then

if (g(x))² = g(x), then

thus

and g(x) = g₀, that is, an element of F_p (Property 2.9(3)).