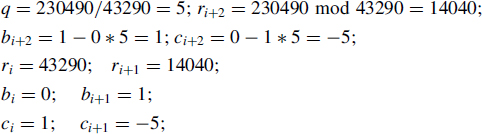2.1 NUMBER THEORY

2.1.1 Basic Definitions

Definitions 2.1

1. The set of natural numbers¹ N = {0, 1, 2, 3, …}.
2. The set of integers Z = {…, −3, −2, −1, 0, 1, 2, 3, … }.

Definition 2.2 Given two integers x and y, y divides x (y is a divisor of x) if there exists an integer z such that x = z.y.

Definition 2.3 Given two integers x and y, with y > 0, there exist two integers q (the quotient) and r (the remainder) such that

It can be proved that q and r are unique. Then (notation)

An alternative definition is the following.

Definition 2.4 (Integer Division) Given two integers x and y, with y > 0, there exist two integers q (the quotient) and r (the remainder) such that

It can be proved that q and r are unique. Then (notation)

Examples 2.1

1. x = −16, y = 3:

   

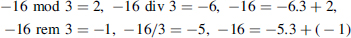
2. x = −15, y = 3:

   

Definitions 2.5

1. Given two integers x and y, z is the greatest common divisor of x and y if
   • z is a natural number (nonnegative integer),
   • z divides both x and y,
   • any other common divider of x and y is also a divider of z.

   Notation: z = gcd(x, y).

2. Given two integers x and y, they are said to be relatively prime if gcd(x, y) = 1.
3. An integer p > 1 is said to be prime if its only positive divisors are 1 and p.

2.1.2 Euclidean Algorithms

Given two natural numbers x and y, the Euclidean algorithm for natural numbers computes gcd(x, y). It is based on a series of integer divisions:

Observe that any divider of r(i − 1) and r(i) is also a divider of r(i) and r(i + 1) so that

Initially,

Then compute

where r(1) > r(2) … > r(n) = 0 and gcd(r(i − 1), r(i)) = gcd(r(i), r(i + 1)), so that

Example 2.2 Let r(0) = x = 8580; r(1) = y = 4070;

Then gcd(8580,4070) = 110.

In the extended Euclidean algorithm a series of coefficients b(i) and c(i) are calculated in parallel with the computation of r(0), r(1), r(2), … , r(n):

It can be demonstrated by induction that

In particular,

In conclusion, the extended Euclidean algorithm expresses the greatest common divisor z of two natural numbers x and y as a linear combination of x and y, that is,

Algorithm 2.1 Extended Euclidean Algorithm

if x=0 then z:=y; b:=0; c:=1;
elsif y=0 then z:=x; b:=1; c:=0;
else
  r_i:=x; r_iplus1:=y; b_i:=1; c_i:=0; b_iplus1:=0;
    c_iplus1:=1;
  while r_iplus1>0 loop
      q:=r_i/r_iplus1; r_iplus2:=r_i mod r_iplus1;
      b_iplus2:=b_i-b_iplus1*q; c_iplus2:=c_i-c_iplus1*q;
      r_i:=r_iplus1; r_iplus1:=r_iplus2;
      b_i:=b_iplus1; b_iplus1:=b_iplus2;
      c_i:=c_iplus1; c_iplus1:= c_iplus2;
     end loop;
     z:=r_i; b:=b_i; c:=c_i;
  end if;

Example 2.3 Let r_i = x = 230490; r_i+1 = y = 43290; b_i = c_i+1 = 1; b_i+1 = c_i = 0.

• Step 1:

  

• Step 2:

  

• Step 3:

  

2.1.3 Congruences

Definition 2.6 Given two integers x and y, and a positive integer n, x is congruent to y modulo n if n divides the difference (x − y).

Notation:

Property 2.1 (Basic Properties of Congruences)

1. x ≡ y (mod n) if and only if (x mod n) = (y mod n) (Definition 2.3).
2. The relation x ≡ y (mod n) is an equivalence relation (reflexive, symmetric, and transitive).
3. If x₁ ≡ y₁ (mod n) and x₂ ≡ y₂ (mod n), then

   

From Properties 2.1(1 and 2), it can be seen that the mod n congruence relation partitions Z into n equivalence classes. Each equivalence class contains exactly one element of the set {0, 1, 2, …, n − 1}, namely, the common value (x mod n) for all elements x of the class. Furthermore, according to Property 2.1(3), the addition, subtraction, and multiplication of congruence classes can be defined. As a matter of fact, the set of equivalence classes is isomorphic to

where the addition, the subtraction, and the multiplication are defined by

Definition 2.7 Given two elements x and y of Z_n such that x.y = 1, then y is said to be the multiplicative inverse of x. If such an inverse exists, it is unique.

Notation:

Property 2.2 x has a multiplicative inverse if and only if gcd(x, n) = 1.

Proof If x.y = 1 mod n, then x.y = q.n + 1 so that any divisor of x and n is also a divisor of 1. Thus gcd(x, n) = 1.

If gcd(x, n) = 1, then (relation (2.1)) there exist b and c such that 1 = b.x + c.n, so that x⁻¹ = b.

More generally, we have the following.

Properties 2.3

1. Let g = gcd(a, n). Then the equation a.x ≡ d (mod n) has a solution x if and only if g divides d.
2. The solutions of a.x ≡ d (mod n) are the same as the solutions of (a/g).x ≡ (d/g) (mod n/g).
3. There are g solutions, all of them congruent modulo n/g.

Proof

1. If ax ≡ d (mod n), then a.x − d = q.n. As g divides both a and n, it also divides d. If g divides d, then d = q.g. According to (2.1), g is a linear combination of a and n; that is, g = b.a + c.n. So d = q(b.a + c.n) and x = q.b is a solution.
2. If g divides d and a.x ≡ d (mod n), that is, a.x − d = q.n, then (a/g).x − (d/g) = q.(n/g) and (a/g).x ≡ (d/g) (mod n/g). Inversely, if (a/g).x ≡ (d/g) (mod n/g) then a.x ≡ d (mod n).
3. As a/g and n/g are relatively prime, then there is a unique solution within Z_n/g, namely, x = x₀ = (d/g).(a/g)⁻¹ mod n/g. The complete set of solutions within Z_n is

   

   Observe that if k < g and x₀ < (n/g), then x_k ≤ (n/g) − 1 + (g − 1).(n/g) = n − 1.

Properties 2.4 (Chinese Remainder Theorem) Consider s pairwise relatively prime integers m₁, m₂, …, m_s whose product is equal to M. Then the system

has a unique solution N within Z_M (|a|_m stands for a mod m):

where

The r_i are called residues modulo m_i.

Proof In order to compute a solution of system (2.3) observe that every m_i is relatively prime with every m_j (j ≠ i) so that every m_j is relatively prime with = M/m_j. Then has a multiplicative inverse and

is obviously a solution. The uniqueness is deduced from the fact that different systems have different solutions, and that there are exactly as many different systems as elements in Z_M.

The computation of ()⁻¹mod m_i can be performed with the extended Euclidean algorithm: as m_i is relatively prime with M/m_j, the algorithm generates b and c such that

and

Garner's algorithm 2.2 ([GAR1959], [MEN1996]) computes N using a technique slightly different from the straight computation of (2.4). It computes first the mixed-radix digits within a preliminary step of a procedure step computing the base-B digits through a mixed-radix to base-B conversion (see mixed-radix system—Chapter 3).

A procedure inversion_step using the Euclidean algorithm to compute (m_j)⁻¹ mod m_i is first defined as

procedure inversion_step (m(j), m(i): in natural; invm(j): out natural);

Algorithm 2.2 Garner's Algorithm

Assume N is given, according to (2.3), by its set of residues r_i = N mod m_i:

for i in 2..s loop
   c(i):=1;
   for j in 1..(i-1) loop
     inversion_step (m(j), m(i), invm(j));
     c(i):=invm(j)*c(i) mod m(i);
   end loop;
end loop;
u:=r(1); x:=u; b(1):=1;
for i in 2..s loop
   b(i):=b(i-1)*m(i-1);
  end loop;
  for i in 2..s loop
     u:=(r(i) 2 x)*c(i) mod m(i);
     x:=x+u*b(i);
  end loop;

Examples 2.4

1. Let {r_i} = {1, 2, 3, 4, 5} be the set of remainders (residual expression) of a natural number N with respect to the respective set of moduli {m_i} = {2, 3, 5, 7, 11}. To compute the base-10 expression of N using (2.4), one first needs to compute {} and {1/ mod m_i}. A straightforward base-10 calculation leads to

   

   while the Euclidean algorithm is used to compute

   

   Formula (2.4) yields

   

2. Garner's algorithm is now used to solve the same problem. The Euclidean algorithm is used in the first loop of Algorithm 2.2. It computes:

   

   The second loop computes the weights b(j) as

   

   The third loop finally computes x as

   

Observe that the first two loops are independent and therefore may be computed in parallel. Moreover, if the modulus system is fixed, the c(i) and b(i) are computed once then stored for further use.

Definitions 2.8

1. The set of elements x of Z_n relatively prime with n is the multiplicative group :

   

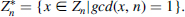
2. The Euler phi function ϕ(n) is the number of elements in .

According to Property 2.2, is the set of invertible elements of Z_n. In particular, if p is a prime number then

Properties 2.5 (Fermat's Little Theorem) Let p be a prime.. Any integer x satisfies x^p ≡ x (mod p), and any integer x not divisible by p satisfies x^p−1 ≡ 1 (mod p).

Proof If x is not divisible by p and if i..x ≡ j.x (mod p), that is, (i − j).x = q.p, then i ≡ j (mod p). Thus

as the p − 1 above multiples of x are distinct and nonzero, they must be congruent to 1, 2, 3, … , p − 1 in some order.

So

or

As p does not divide (p − 1)!,

that is,

If x is divisible by p, then x^p ≡ x ≡ 0 (mod p).

Corollary 2.1 Let p be a prime.. If x is not divisible by p and if r ≡ s (mod p − 1), then

Proof Assume that r > s. Then r = q.(p − 1) + s and 1 ≡ 1^q ≡ (x^p−1)^q ≡ x^r−s (mod p), so that x^r ≡ x^s (mod p).

Definitions 2.9

1. The order of an element x of is the least positive integer t such that x^t ≡ 1 (mod n).
2. If the order of x is equal to the number ϕ(n) of elements in , then x is said to be a generator or primitive element of .
3. If has a generator, then is said to be cyclic.

Observe that if x is a generator then = {x¹, x², x³, … , x^ϕ(n)}.

Example 2.5

• Z₇ = {0, 1, 2, 3, 4, 5, 6} and 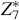= {1, 2, 3, 4, 5, 6};
• 7 is prime and ϕ(7) = 6;
• 1¹ ≡ 1 (mod 7), 2³ ≡ 1 (mod 7), 3⁶ ≡ 1 (mod 7), 4³ ≡ 1 (mod 7), 5⁶ ≡ 1 (mod 7), 6² ≡ 1 (mod 7).

  There are two generators: 3 and 5. For example,

• 3¹ ≡ 3 (mod 7), 3² ≡ 2 (mod 7), 3³ ≡ 6 (mod 7), 3⁴ ≡ 4 (mod 7), 3⁵ ≡ 5 (mod 7), 3⁶ ≡ 1 (mod 7).